Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-22T21:12:54.951Z Has data issue: false hasContentIssue false
  • English
  • Français

On the structure of semialgebraic sets over p-adic fields

Published online by Cambridge University Press:  12 March 2014

Philip Scowcroft  and
Lou van den Dries
Philip Scowcroft
Affiliation:
Department of Mathematics, Yale University, New Haven, Connecticut 06520
Lou van den Dries*
Affiliation:
Department of Mathematics, Stanford University, Stanford, California 94305
*
Department of Mathematics, University of Illinois, Urbana, Illinois 61801
Get access Rights & Permissions [Opens in a new window]

Extract

In his Singular points of complex hypersurfaces Milnor proves the following “curve selection lemma” [10, p. 25]:

Let V ⊂ R m be a real algebraic set, and let U ⊂ R m be an open set defined by finitely many polynomial inequalities:

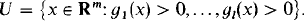
Lemma 3.1. If U ∩ V contains points arbitrarily close to the origin (that is if 0 ∈ Closure (U ∩ V)) then there exists a real analytic curve

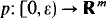
with p(0) = 0 and with p(t) ∈ U ∩ V for t > 0.

Of course, this result will also apply to semialgebraic sets (finite unions of sets U ∩ V), and by Tarski's theorem such sets are exactly the sets obtained from real varieties by means of the finite Boolean operations and the projection maps R n+1 → R n . If, in this tiny extension of Milnor's result, we replace ‘R’ everywhere by ‘Q p ’, we obtain a p-adic curve selection lemma, a version of which we will prove in this essay. Semialgebraic sets, in the p-adic context, may be defined just as they are over the reals: namely, as those sets obtained from p-adic varieties by means of the finite Boolean operations and the projection maps 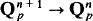. Analytic maps are maps whose coordinate functions are given locally by convergent power series.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 53 , Issue 4 , December 1988 , pp. 1138 - 1164
Copyright
Copyright © Association for Symbolic Logic 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Abhyankar, S. S., Local analytic geometry, Academic Press, New York, 1964.Google Scholar
[2] Amice, Y., Les nombres p-adiques, Presses Universitaires de France, Paris, 1975.Google Scholar
[3] Bôcher, M., Introduction to higher algebra, Macmillan, New York, 1907.Google Scholar
[4] Collins, G. E., Quantifier elimination for real closed fields by cylindrical algebraic decomposition, Automata theory and formal languages: second GI conference, Kaiserslautern, 1975 (Brakhage, H., editor), Lecture Notes in Computer Science, vol. 33, Springer-Verlag, Berlin, 1975, pp. 134–183.CrossRefGoogle Scholar
[5] Denef, J., The rationality of the Poincaré series associated to the p-adic points on a variety, Inventiones Mathematicae, vol. 77 (1984), pp. 1–23.CrossRefGoogle Scholar
[6] van den Dries, L., Algebraic theories with definable Skolem functions, this Journal, vol. 49 (1984), pp. 625–629.Google Scholar
[7] Hensel, K. and Landsberg, G., Theorie der algebraischen Funktionen einer Variabeln, und ihre Anwendungen auf algebraische Kurven und Abelsche Integrale, Teubner, Leipzig, 1902.Google Scholar
[8] Hodge, W. V. D. and Pedoe, D., Methods of algebraic geometry, Vol. 2, Cambridge University Press, Cambridge, 1968.Google Scholar
[9] Macintyre, A., On definable sets of p-adic fields, this Journal, vol. 41 (1976), pp. 605–610.Google Scholar
[10] Milnor, J., Singular points of complex hypersurfaces, Princeton University Press, Princeton, New Jersey, 1968.Google Scholar
[11] Milnor, J., Topology from the differentiable viewpoint, University of Virginia Press, Charlottesville, Virginia, 1969.Google Scholar
[12] Prestel, A. and Roquette, P., Formally p-adic fields, Lecture Notes in Mathematics, vol. 1050, Springer-Verlag, Berlin, 1984.CrossRefGoogle Scholar
[13] Scowcroft, P., Definable functions on p-adic fields. Preliminary report, Abstracts of Papers Presented to the American Mathematical Society, vol. 6 (1985), pp. 224–225.Google Scholar
[14] Spivak, M., Calculus on manifolds, Benjamin, New York, 1965.Google Scholar
[15] Walker, R. J., Algebraic curves, Princeton University Press, Princeton, New Jersey, 1950.Google Scholar
[16] Weispfenning, V., Quantifier elimination and decision procedures for valued fields, Models and sets: proceedings of the logic colloquium held in Aachen, July 18–23, 1983, part 1 (Müller, G. H. and Richter, M. M., editors), Lecture Notes in Mathematics, vol. 1103, Springer-Verlag, Berlin, 1984, pp. 419–472.CrossRefGoogle Scholar
[17] Zariski, O. and Samuel, P., Commutative algebra, vol. 2, Van Nostrand, Princeton, New Jersey, 1960.CrossRefGoogle Scholar
[18] Zimmer, R. J., Ergodic theory and semisimple groups, Birkhäuser, Basel, 1984.CrossRefGoogle Scholar