Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-31T20:29:25.006Z Has data issue: false hasContentIssue false
  • English
  • Français

Souslin forcing

Published online by Cambridge University Press:  12 March 2014

Jaime I. Ihoda  and
Saharon Shelah
Jaime I. Ihoda
Affiliation:
Department of Mathematics, University of California, Berkeley, California 94720
Saharon Shelah
Affiliation:
Universidad Católica De Chile, Santiago, Chile Institute of Mathematics, The Hebrew University, Jerusalem, Israel Department of Mathematics, Rutgers University, New Brunswick, New Jersey 08903
Get access Rights & Permissions [Opens in a new window]

Abstract

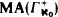We define the notion of Souslin forcing, and we prove that some properties are preserved under iteration. We define a weaker form of Martin's axiom, namely , and using the results on Souslin forcing we show that 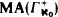is consistent with the existence of a Souslin tree and with the splitting number s = ℵ1. We prove that 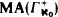proves the additivity of measure. Also we introduce the notion of proper Souslin forcing, and we prove that this property is preserved under countable support iterated forcing. We use these results to show that ZFC + there is an inaccessible cardinal is equiconsistent with ZFC + the Borel conjecture + 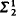-measurability.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 53 , Issue 4 , December 1988 , pp. 1188 - 1207
Copyright
Copyright © Association for Symbolic Logic 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCE

[Ba] Baumgartner, J. E., Iterated forcing, Surveys in set theory (Mathias, A. R. D., editor), London Mathematical Society Lecture Note Series, vol. 87, Cambridge University Press, Cambridge, 1983, pp. 1–59.Google Scholar
[Ca] Carlson, T., The dual Borel conjecture (unpublished notes).Google Scholar
[Fr] Fremlin, D., Consequences of Martin's axiom, Cambridge Tracts in Mathematics, vol. 84, Cambridge University Press, Cambridge, 1984.CrossRefGoogle Scholar
[GPS] Galvin, F., Prikry, K. and Solovay, R., Strong measure zero sets, Notices of the American Mathematical Society, vol. 26 (1979), p. A–280.Google Scholar
[Ih1] Ihoda, J., Some consistency results on projective sets of reals, Israel Journal of Mathematics (submitted).Google Scholar
[Ih2] Ihoda, J., -sets of reals, this Journal, vol. 53 (1988), pp. 636–642.Google Scholar
[Ih3] Ihoda, J., Strong measure zero sets and rapid filters, this Journal, vol. 53 (1988), pp. 393–402 Google Scholar
[Je] Jech, T., Set theory, Academic Press, New York, 1978.Google Scholar
[Ke] Keisler, H. J., Logic with the quantifier “there exist uncountably many”, Annals of Mathematical Logic, vol. 1 (1970), pp. 1–93.CrossRefGoogle Scholar
[La] Laver, R., On the consistency of Borel's conjecture, Acta Mathematica, vol. 137 (1976), pp. 151–169.CrossRefGoogle Scholar
[Mi] Miller, A., Some properties of measure and category, Transactions of the American Mathematical Society, vol. 266 (1981), pp. 93–114.CrossRefGoogle Scholar
[MS] Martin, D. and Solovay, R., Internal Cohen extensions, Annals of Mathematical Logic, vol. 2 (1970), pp. 143–178.CrossRefGoogle Scholar
[Ra] Raisonnier, J., A mathematical proof of S. Shelah's theorem on the measure problem and related results, Israel Journal of Mathematics, vol. 48 (1984), pp. 48–56.CrossRefGoogle Scholar
[RS] Raisonnier, J. and Stern, J., The strength of measurability hypotheses, Israel Journal of Mathematics, vol. 50(1985), pp. 337–349.CrossRefGoogle Scholar
[Sh1] Shelah, S., Can you take Solovay's inaccessible away? Israel Journal of Mathematics, vol. 48 (1984), pp. 1–47.CrossRefGoogle Scholar
[Sh2] Shelah, S., Proper forcing, Lecture Notes in Mathematics, vol. 940, Springer-Verlag, Berlin, 1982.CrossRefGoogle Scholar
[Sh3] Shelah, S., On cardinal invariants of the continuum, Axiomatic set theory (Baumgartner, J. E. et al., editors), Contemporary Mathematics, vol. 31, American Mathematical Society, Providence, Rhode Island, 1984, pp. 183–207.CrossRefGoogle Scholar