This paper is a continuation of An abstract form of the Church-Rosser theorem. I (this Journal, vol. 35 (1969), pp. 545–560). In Part I, the Church-Rosser property was deduced from abstract premises (A1)–(A8). The original draft of Part II contained some applications of this result, and a fairly simple abstract result by which the Church-Rosser property could be extended from λβ-reduction to λβη-reduction (Curry's notation [3, Chapter 3]). But since this draft was written, these results have been obtained independently and improved by other workers, and a simple and natural new proof for λβ-reduction has been discovered by W. W. Tait and P. Martin-Löf (see §11 later, and [17, §2.4.3]).

So the main purpose of the present Part II is merely to justify the claim in Part I that the abstract theorem does cover the case of λβ-reduction (and various modifications). I shall also include a summary of the main kinds of Church-Rosser proofs. The paragraph and theorem numbers in Part II will continue from those of Part I.

In §§5 and 6 below, Theorem 1 will be specialised to reductions defined by replacements of parts of expressions by others (Theorems 2 and 2A). At the end of §6 an important subclass of such reductions will be treated (Theorem 3).

In §7, Theorem 3 will be applied to prove the Church-Rosser property for combinatory weak reduction [10, §11B], with or without type-restrictions and extra “arithmetical” reduction-rules (Theorems 4 and 5). (In the original draft Theorem 5 was deduced directly from Theorem 2A; the present intervening Theorem 3 is an independent result of B. Rosen [7].)

Some negative results will be proved concerning the following for certain infinitary languages ℒ1 and ℒ2.

Definition. Beth(ℒ1, ℒ2) iff, for every sentence ϕ(R) of ℒ1, and n-place relation symbols R and S such that S does not occur in ϕ(R), if

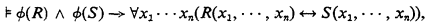
then there is an ℒ2 formula θ(x1, …, xn) such that

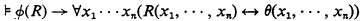
and θ is built up using only those constant and relation symbols of ϕ other than R.

That is, Beth(ℒ1, ℒ2) iff for every implicit ℒ1 definition ϕ(R) of relations, there is a corresponding explicit ℒ2 definition θ. Beth(ℒωω, ℒωω) was proved by Beth.

Malitz proved that not Beth(ℒω1 ω1, ℒ∞∞) (hence not Beth (ℒ∞∞, ℒ∞∞)), but Beth (ℒ∞ω, ℒ∞∞). In §1, it is shown that Beth(ℒ∞ω, ℒ∞ω) is false. In §2, we strengthen this by showing that, for every cardinal κ, not Beth(ℒ∞ω, ℒ∞κ). In fact, not Beth (ℒκ+ω, ℒ∞κ) follows from property A(κ) defined in §2, and A(κ) is known for regular κ > ω (unpublished result of Morley).

More information on infinitary Beth and Craig theorems is given in [2] and [3]. We assume that the reader is acquainted with the languages ℒκλ which allow conjunctions over ≺κ formulas and quantifiers over ≺λ variables. Thus, we assume that the reader is acquainted with the back and forth argument for showing that two structures are ≡∞κ (ℒ∞κ-elementarily equivalent). Our notation is fairly standard.

In [2], Prikry showed that if κ is a weakly inaccessible cardinal which carries a Rowbottom filter, then there is a Boolean extension of V (the universe), having the same cardinals as V, in which cf(κ) = ω. In this note, we obtain necessary and sufficient conditions which a filter D on κ must possess in order that this may be done.

There are two main lacunae in recent work on modal logic: a lack of general results and a lack of negative results. This or that logic is shown to have such and such a desirable property, but very little is known about the scope or bounds of the property. Thus there are numerous particular results on completeness, decidability, finite model property, compactness, etc., but very few general or negative results.

In these papers I hope to help fill these lacunae. This first part contains a very general completeness result. Let In be the axiom that says there are at most n incomparable points related to a given point. Then the result is that any logic containing K4 and In is complete.

The first three sections provide background material for the rest of the papers. The fourth section shows that certain models contain no infinite ascending chains, and the fifth section shows how certain elements can be dropped from the canonical model. The sixth section brings the previous results together to establish completeness, and the seventh and last section establishes compactness, though of a weak kind. All of the results apply to the corresponding intermediate logics.

The cardinality problem for ultraproducts is as follows: Given an ultrafilter over a set I and cardinals αi, i ∈ I, what is the cardinality of the ultraproduct ? Although many special results are known, several problems remain open (see [5] for a survey). For example, consider a uniform ultrafilter over a set I of power κ (uniform means that all elements of have power κ). It is open whether every countably incomplete has the property that, for all infinite α, the ultra-power has power ακ. However, it is shown in [4] that certain countably incomplete , namely the κ-regular , have this property.

This paper is about another cardinality property of ultrafilters which was introduced by Eklof [1] to study ultraproducts of abelian groups. It is open whether every countably incomplete ultrafilter has the Eklof property. We shall show that certain countably incomplete ultrafilters, the κ-good ultrafilters, do have this property. The κ-good ultrafilters are important in model theory because they are exactly the ultrafilters such that every ultraproduct modulo is κ-saturated (see [5]).

Let be an ultrafilter on a set I. Let αi, n, i ∈ I, n ∈ ω, be cardinals and αi, n, ≥ αi, m if n < m. Let

.

Then ρn are nonincreasing and therefore there is some m and ρ such that ρn = ρ if n ≥ m. We call ρ the eventual value (abbreviated ev val) of ρn.

The application of priority arguments to study the structure of the upper semilattice of α-r.e. α-degrees for all admissible ordinals α was first done successfully by Sacks and Simpson [5] who proved that there exist incomparable α-r.e. α-degrees. Lerman and Sacks [3] studied the existence of minimal pairs of α-r.e. α-degrees, and proved their existence for all admissible ordinals α which are not refractory. We continue the study of the α-r.e. α-degrees, and prove that no minimal pair of α-r.e. α-degrees can have as least upper bound the complete α-r.e. α-degree.

The above-mentioned theorem was first proven for α = ω by Lachlan [1]. Our proof for α = ω differs from Lachlan's in that we eliminate the use of the recursion theorem. The proofs are similar, however, and a knowledge of Lachlan's proof will be of considerable aid in reading this paper.

We assume that the reader is familiar with the basic notions or α-recursion theory, which can be found in [2] or [5].

Throughout the paper a will be an arbitrary admissible ordinal. We identify a set A ⊆ α with its characteristic function, A(x) = 1 if x ∈ A, and A(x) = 0 if x ∉ A.

If A ⊆ α and B ⊆ α, then A ⊕ B will denote the set defined by

A ⊕ B(x) = A(y) if x = λ + 2z, λ is a limit ordinal, z < ω and y = λ + z,

= B(y) if x = λ + 2z + 1, λ is a limit ordinal, z < ω, and y = λ + z.

In [4], Kunen used iterated ultrapowers to show that if U is a normal κ-complete nontrivial ultrafilter on a cardinal κ then L[U], the class of sets constructive from U, has only the ultrafilter U ∩ L[U] and this ultrafilter depends only on κ. In this paper we extend Kunen's methods to arbitrary sequences U of ultrafilters (provided that they fulfill a coherency condition) and obtain generalizations of these results (§3). In particular we answer Problem 1 of Kunen and Paris [5] which asks whether the number of ultrafilters on κ can be intermediate between 1 and 22κ. If there is a normal κ-complete ultrafilter U on κ such that {α < κ: α is measurable} ∈ U then there is an inner model with exactly two normal ultrafilters on κ, and if κ is super-compact then there are inner models having κ+ +, κ+ or any cardinal less than or equal to κ normal ultrafilters (§4).

These methods also show that several properties of L which had been shown to hold for L[U] also hold for L[U]: using an idea of Silver we show that in L[U] the generalized continuum hypothesis is true, there is a Souslin tree, and there is a well-ordering of the reals. In addition we generalize a result of Kunen to characterize the countaby complete ultrafilters of L[U].

The intuitionistic propositional logic I has the following (disjunction) property

.

We are interested in extensions of the intuitionistic logic which are both decidable and have the disjunction property. Systems with the disjunction property are known, for example the Kreisel-Putnam system [1] which is I + (∼ϕ → (ψ ∨ α))→ ((∼ϕ→ψ) ∨ (∼ϕ→α)) and Scott's system I + ((∼ ∼ϕ→ϕ)→(ϕ ∨ ∼ϕ))→ (∼∼ϕ ∨ ∼ϕ). It was shown in [3c] that the first system has the finite-model property.

In this note we shall construct a sequence of intermediate logics Dn with the following properties:

These systems are presented both semantically and syntactically, using the remarkable correspondence between properties of partially ordered sets and axiom schemata of intuitionistic logic. This correspondence, apart from being interesting in itself (for giving geometric meaning to intuitionistic axioms), is also useful in giving independence proofs and obtaining proof theoretic results for intuitionistic systems (see for example, C. Smorynski, Thesis, University of Illinois, 1972, for independence and proof theoretic results in Heyting arithmetic).

There is a PCA well-ordering of the real line if and only if there is a real from which every real is constructible.

This paper constitutes a short report on the proof theory which developed in the course of an investigation of Essenin-Volpin's foundational studies (see his paper in Infinitistic methods.) The Infinitistic methods paper is primarily concerned with proving the consistency of ZF. His arguments employ some very unusual ideas, especially that of the possibility of different length natural number series. The modal setting which he uses for these ideas and which is really all important is not reflected in the present paper. Only a simple representation of this idea is considered, namely, the use of *N, the nonstandard natural numbers, together with N, the standard natural numbers, to play the roles of a “long” and a “short” number series.

It will be useful to make a few general remarks before beginning on the technical details. These remarks are especially directed towards those people who have read Essenin-Volpin's work, the above-mentioned paper in particular and the one appearing in the proceedings of the 1968 Conference on Intuitionism and Proof Theory at Buffalo, New York.

I want to draw a comparison between the ultra-intuitionistic position of Essenin-Volpin on the one hand with the intuitionistic and realistic positions on the foundations of mathematics on the other hand. Intuitionism makes a transition from the traditional mathematical position (realism) that the rules of mathematical reasoning must be constructed so as to preserve truth (as known by an omniscient being about “the real world” of abstract mathematical objects) to the position that the rules of mathematical reasoning must be in accord with the process of knowing (performed by the “ideal mathematician” or “creative subject”) about the world of mental constructions. Ultra-intuitionism deepens and extends this transition to the position that the fundamental rules of mathematical reasoning must be in accord with processes of knowing accessible to human beings.

Shoenfield [6] constructed a hierarchy for any type two object F in which 2E is recursive by generalizing the hyperarithmetical hierarchy, using a jump operation jF defined by

(A similar hierarchy was constructed independently by Hinman [3].) In order to construct a hierarchy for an arbitrary type two F we must first associate with F an operator which, on one hand will always be recursive in F, and on the other hand will generate all the functions recursive in F when iterated over a simultaneously generated set of ordinal notations OF. Clearly the use of 2E in the above definition of jF(f) can be avoided if, instead of diagonalizing F over all functions recursive in f, we only diagonalize F over, say, the functions primitive recursive in f. If furthermore we code in a function which enumerates all functions primitive recursive in f then the resulting operation will certainly generate a primitive recursively expanding hierarchy of functions recursive in F. The problem that remains is whether this hierarchy will exhaust the 1-section of F. But this reduces to an effectiyized version of the following problem: If g is recursive in some level of the hierarchy, is g primitive recursive in some higher level ? An affirmative answer is suggested by the completeness results of Feferman [2], and our main theorem below will be proved by combining his ideas with those of Shoenfield [6]. The result is a hierarchy which applies to all type two objects, and which replaces the notion of recursion in F by the simpler notion of primitive recursion in certain functions generated by F. Unfortunately, in contrast with the Shoenfield hierarchy, the hierarchy developed here cannot always be expected to have the uniqueness property (even w.r.t. ≤T), and for this reason the proof of our main theorem is rather more complicated than the corresponding proof in [6].

Let be the collection of all sets which are finite Boolean combinations of recursively enumerable (r.e.) sets of numbers. Dale Myers asked [private correspondence] whether there exists a nonempty class of sets containing no member of . In this note we construct such a class. The motivation for Myers' question was his observation (reported in [1]) that the existence of such a class is equivalent to the assertion that there is a finite consistent set of tiles which has no m-trial tiling of the plane for any m (obeying the “origin constraint”). (For explanations of these terms and further results on tilings of the plane, cf. [1] and [5].) In addition to the application to tilings, the proof of our results gives some information on bi-immune sets and on complete extensions of first-order Peano arithmetic.

A class of sets may be roughly described as the class of infinite binary input tapes for which a fixed Turing machine fails to halt, or alternatively as the class of infinite branches of a recursive tree of finite binary sequences. (In these definitions, sets of numbers are identified with the corresponding binary sequences.) Precise definitions, as well as many results concerning such classes, may be found in [3] and [4].

This work is an attempt to characterize the index sets of classes of recursively enumerable sets which are expressible in terms of open sets in the Baire topology on the power set of the set N of natural numbers, usual in recursion theory. Let be a class of subsets of N and be the set of indices of recursively enumerable sets Wх belonging to .

A well-known theorem of Rice and Myhill (cf. [5, p. 324, Rice-Shapiro Theorem]) states that is recursively enumerable if and only ifis a r.e. open set. In this case, note that if is not empty and does not contain all recursively enumerable sets, is a complete set. This theorem will be partially extended to classes which are boolean combinations of open sets by the following:

(i) There is a canonical boolean combination which represents, namely the shortest among boolean combinations which represent.

(ii) The recursive isomorphism type of depends on the length n of this canonical boolean combination (and trivial properties of ); for instance, is recursively isomorphic (in the particular case where is a boolean combination of recursive open sets) to an elementary set combination Yn or Un, constructed from {х ∣ х Wх) and depending on the length n. We can say also that is a complete set in the sense of Ershov's hierarchy [1] (in this particular case).

Let σ be any sequence B0, B1 …, Bn, … of transitive sets closed under pairs with for each n. In this paper we show that the smallest admissible set Aσ with σ ∈ Aσ is Σ1 compact. Thus we have an entirely new class of explicitly describable uncountable Σ1 compact sets.

The search for uncountable Σ1 compact languages goes back to Hanf's negative results on compact cardinals [7]. Barwise first showed that all countable admissible sets were Σ1 compact [1] and then went on to give a characterization of the Σ1 compact sets in terms of strict reflection [2]. While his characterization has been of interest in understanding the Σ1 compactness phenomenon it has led to the identification of only one class of uncountable Σ1 compact sets. In particular, Barwise showed [2], using the above notation, that if ⋃nBn is power set admissible it satisfies the strict reflection principle and hence is Σ1 compact. (This result was obtained independently by Karp using algebraic methods [9].)

In proving our compactness theorem we follow Makkai's approach to the Barwise Compactness Theorem [12] and use a modified version of Smullyan's abstract consistency property [14]. A direct generalization of Makkai's method to the cofinality ω case yields a proof of the Barwise-Karp result mentioned above [6]. In order to obtain our new result we depart from the usual definition of language and use instead the indexed languages of Karp [9] in which a conjunction is considered to operate on a function whose range is a set of formulas rather than on a set of formulas itself.

The concept of model completeness has been very useful in model theory. In this article we obtain a new model theoretic tool by “reversing the arrows.” Specifically, model completeness deals with the relations between a model of a theory and its extensions; in this paper we shall be concerned with the relation between a model of a theory and its homomorphic pre-images.

This work is based on the intuitive principle that metamathematical theorems about universal sentences of the lower predicate calculus and substructures can be translated in a truth-preserving way to theorems about positive sentences and homomorphic images. From model completeness and the completeness theorems which depend on it, this translation gives new criteria for completeness.

Special thanks are due to Professor A. Robinson whose encouragement and suggestions have contributed much to these results.

In [1] we proved the following interpolation theorem for first-order (finitary) logic:

Theorem (Scott). Let A and B be sentences. There is an -sentence C such that A → C and C → B iff whenever and are -isomorphic structures and satisfies A then satisfies B.

We show here that the Theorem holds for A and B in Lω1, ω only if we permit the interpolant C to be in L(2ω)+, ω, where (2ω)+ is the successor of 2ω.

Our language contains the usual logical symbols and the relation symbols Ri, is i ∈ J. IfI ⊆ J define an I-sentence to be a sentence containing only relations with subscripts in I. If define an -sentence to be a boolean combination of I-sentences with , i.e., a sentence consisting of I-sentences, for various I's in , joined together by ∨, ∧ and ⌝; e.g., ∀xR1(x) ∨ ∀xR2(x)is a{{1}, {2}}-sentence but ∀x(R1(x) ∨ R2(x)) is not. If is a structure let , be the structure obtained by restricting to just the relations with subscripts in I. We say that is -isomorphic to if is isomorphic to for each .

Let be the set of recursive functions computable by machines using at most t(x) computation steps on argument x, for all but finitely many inputs x. We call t a name for the complexity class . Suppose we allow our machines to run longer, say h(x, t(x)) steps on argument x, where h is some fixed recursive function. One might expect that, for large enough h, permitting our machines to run longer by an amount h will always allow us to compute new functions, i.e., is a proper subset of . This turns out not to be the case: The “gap theorem” ([2], [3]) implies that for every recursive h there exists a recursive t such that . However, if we restrict our attention to names from a certain subclass of the recursive functions, then we can indeed uniformly increase the size of our -classes. Informally, we call a recursive function t “honest” if some machine computes t(x) in roughly t(x) steps for each argument x. (A precise definition is given in Definition 1 below.) Then according to the “compression theorem” [1], there exists a single recursive function h such that, for every honest t, is a proper subset of . Thus the phenomenon of the gap theorem is avoided by restricting attention to honest functions. It is a surprising consequence of the “honesty theorem” of McCreight and Meyer ([4], [5]) that there is no loss of generality in this restriction. Namely, for any recursive function t there is an honest recursive function t′ such that .

H. Scholz [11] defined the spectrum of a formula φ of first-order logic with equality to be the set of all natural numbers n for which φ has a model of cardinality n. He then asked for a characterization of spectra. Only partial progress has been made. Computational aspects of this problem have been worked on by Gunter Asser [1], A. Mostowski [9], and J. H. Bennett [2]. It is known that spectra include the Grzegorczyk class and are properly included in . However, no progress has been made toward establishing whether spectra properly include , or whether spectra are closed under complementation.

A possible connection with automata theory arises from the fact that contains just those sets which are accepted by deterministic linear-bounded Turing machines (Ritchie [10]). Another resemblance lies in the fact that the same two problems (closure under complement, and proper inclusion of ) have remained open for the class of context sensitive languages for several years.

In this paper we show that these similarities are not accidental—that spectra and context sensitive languages are closely related, and that their open questions are merely special cases of a family of open questions which relate to the difference (if any) between deterministic and nondeterministic time or space bounded Turing machines.

In particular we show that spectra are just those sets which are acceptable by nondeterministic Turing machines in time 2cx, where c is constant and x is the length of the input. Combining this result with results of Bennett [2], Ritchie [10], Kuroda [7], and Cook [3], we obtain the “hierarchy” of classes of sets shown in Figure 1. It is of interest to note that in all of these cases the amount of unrestricted read/write memory appears to be too small to allow diagonalization within the larger classes.

There is an analogy between concepts such as end-extension types and minimal types in the model theory of Peano arithmetic and concepts such as P-points and selective ultrafilters in the theory of ultrafilters on N. Using the notion of conservative extensions of models, we prove some theorems clarifying the relation between these pairs of analogous concepts. We also use the analogy to obtain some model-theoretic results with techniques originally used in ultrafilter theory. These results assert that every countable nonstandard model of arithmetic has a bounded minimal extension and that some types in arithmetic are not 2-isolated.

We give a direct mathematical proof of the Mathias-Silver theorem that every analytic set is Ramsey.