This work is an attempt to characterize the index sets of classes of recursively enumerable sets which are expressible in terms of open sets in the Baire topology on the power set of the set N of natural numbers, usual in recursion theory. Let 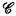be a class of subsets of N and 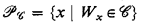be the set of indices of recursively enumerable sets Wх belonging to .

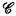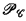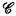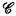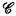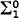A well-known theorem of Rice and Myhill (cf. [5, p. 324, Rice-Shapiro Theorem]) states that is recursively enumerable if and only ifis a r.e. open set. In this case, note that if is not empty and does not contain all recursively enumerable sets, is a complete set. This theorem will be partially extended to classes which are boolean combinations of open sets by the following:

(i) There is a canonical boolean combination which represents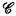, namely the shortest among boolean combinations which represent.

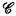(ii) The recursive isomorphism type of 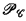depends on the length n of this canonical boolean combination (and trivial properties of 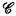); for instance, 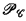is recursively isomorphic (in the particular case where 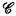is a boolean combination of recursive open sets) to an elementary set combination Yn or Un, constructed from {х ∣ х Wх) and depending on the length n. We can say also that 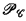is a complete set in the sense of Ershov's hierarchy [1] (in this particular case).