Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-05T15:47:44.805Z Has data issue: false hasContentIssue false
  • English
  • Français

Turing machines and the spectra of first-order formulas

Published online by Cambridge University Press:  12 March 2014

Neil D. Jones  and
Alan L. Selman
Neil D. Jones
Affiliation:
Pennsylvania State University, University Park, Pennsylvania 16802
Alan L. Selman
Affiliation:
Florida State University, Tallahassee, Florida 32306
Get access Rights & Permissions [Opens in a new window]

Extract

H. Scholz [11] defined the spectrum of a formula φ of first-order logic with equality to be the set of all natural numbers n for which φ has a model of cardinality n. He then asked for a characterization of spectra. Only partial progress has been made. Computational aspects of this problem have been worked on by Gunter Asser [1], A. Mostowski [9], and J. H. Bennett [2]. It is known that spectra include the Grzegorczyk class 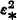and are properly included in 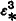. However, no progress has been made toward establishing whether spectra properly include 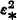, or whether spectra are closed under complementation.

A possible connection with automata theory arises from the fact that 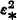contains just those sets which are accepted by deterministic linear-bounded Turing machines (Ritchie [10]). Another resemblance lies in the fact that the same two problems (closure under complement, and proper inclusion of 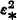) have remained open for the class of context sensitive languages for several years.

In this paper we show that these similarities are not accidental—that spectra and context sensitive languages are closely related, and that their open questions are merely special cases of a family of open questions which relate to the difference (if any) between deterministic and nondeterministic time or space bounded Turing machines.

In particular we show that spectra are just those sets which are acceptable by nondeterministic Turing machines in time 2cx, where c is constant and x is the length of the input. Combining this result with results of Bennett [2], Ritchie [10], Kuroda [7], and Cook [3], we obtain the “hierarchy” of classes of sets shown in Figure 1. It is of interest to note that in all of these cases the amount of unrestricted read/write memory appears to be too small to allow diagonalization within the larger classes.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 39 , Issue 1 , March 1974 , pp. 139 - 150
Copyright
Copyright © Association for Symbolic Logic 1974

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Asser, G., Das Repräsentenproblem im Prädikatenkalkul der ersten Stufe mit Identität, Zeitschrift für mathematische Logik und Grundlagen der Mathematik, vol. 1 (1955), pp. 252–263.CrossRefGoogle Scholar
[2]Bennett, J., On spectra, Doctoral Dissertation, Princeton University, Princeton, N.J., 1962.Google Scholar
[3]Cook, S. A., Characterization of push-down machines in terms of time-bounded computers, Journal of the Association for Computing Machinery, vol. 18 (1971), pp. 4–18.CrossRefGoogle Scholar
[4]Cook, S. A., The complexity of theorem-proving procedures, Third ACM Symposium on Theory of Computing, 1971, pp. 151–158.Google Scholar
[5]Grzegorczyk, A., Some classes of recursive functions, Rozprawy Mathematyczne, vol. 44 (1953), pp. 1–45.Google Scholar
[6]Hartmanis, J. and Stearns, R. E., On the computational complexity of algorithms, Transactions of the American Mathematical Society, vol. 117 (1965), pp. 285–306.CrossRefGoogle Scholar
[7]Kuroda, S. Y., Classes of languages and linear-bounded automata, Information and Control, vol. 7 (1964), pp. 207–223.CrossRefGoogle Scholar
[8]Mager, G., Writing pushdown acceptors, Journal of Computing and Systems Sciences, vol. 3 (1969), pp. 276–319.CrossRefGoogle Scholar
[9]Mostowski, A., Concerning a problem of H. Scholz, Zeitschrift für mathematische Logik und Grundlagen der Mathematik, vol. 2 (1956), pp. 210–214.CrossRefGoogle Scholar
[10]Ritchie, R. W., Classes of predictably computable functions, Transactions of the American Mathematical Society, vol. 106 (1963), pp. 139–173.CrossRefGoogle Scholar
[11]Scholz, H., Problems, this Journal, vol. 17 (1952), p. 160.Google Scholar
[12]Tractenbrot, B. A., Impossibility of an algorithm for the decision problem in finite classes, Doklady Akademii Nauk SSSR, vol. 70 (1950), pp. 569–572.Google Scholar