Throughout the paper A will be a transitive set closed under finite subsets and the formulas in various classes mentioned are allowed to contain parameters from A (or from B in §2).

By use of a refinement of Moschovakis' notion of the game-quantifier [13], [14], [15] we are able to obtain a game-theoretic description of s-Π11 predicates over countable sets which then leads to a classification of positive Σ1 inductive sets.

Similar results are then proved for certain sets of cofinality ω. As a consequence we obtain the compactness results of Green [8], [11], Nyberg [16] and Makkai [12].

The use of games to classify inductive sets was initiated by Moschovakis [13], [14], [15] and has been extended to Q-inductive sets by Aczel [2]. Games were also used in a slightly different setting by Vaught [18] and Makkai [12]. In fact, Vaught's proof of the compactness theorem is very close to our proof in §1 and Makkai's extension to cofinality ω sets uses a result similar to Theorem 3 in §2.

We are indebted to the referee for many helpful suggestions, in particular, for bringing to our attention the related works of Vaught and Makkai cited above.

In this note we give a simple recursive axiomatization for the class of structures of type (ℶω ℵ0). This solves a problem of Vaught which is Problem 13 in the book [1] of Chang and Keisler. The same technique is used to get a recursive axiomatization for the class of κ-like structures where κ is strongly ω-inaccessible.

Let us fix throughout some recursive first-order language L, and until further notice let us suppose that included in L is a distinguished unary predicate symbol U. For cardinals κ and λ with κ ≥ λ ≥ ℵ0, we say the structure has type (κ, λ) if card(A)= κ and card . Let K(κ, λ) be the class of all structures of type (κ, λ). For each ordinal α define 2ακby 20κ = κ, and 2ακ= ⋃ {2λ: λ = 2βκ for some β < α} when α > 0. Let

Vaught proved the following theorem in [7].

Theorem (Vaught). Suppose a is a sentence such that for each n < ω there are κ, λ with κ > 2λn and a model of σ of type (κ, λ). Then whenever κ ≥ λ ≥ ℵ0, the sentence σ has a model of type (κ, λ).

Nonprincipal ultrafilters are harder to define in ZFC, and harder to obtain in ZF + DC, than nonprincipal measures.

The function μ from P(X) to the closed interval [0, 1] is a measure on X if μ. is finitely additive on disjoint sets and μ(X) = 1. (P is the power set.) μ is nonprincipal if μ ({x}) = 0 for each x Є X. μ is an ultrafilter if Range μ= {0, 1}. The existence of nonprincipal measures and ultrafilters on any infinite X follows from the axiom of choice.

Nonprincipal measures cannot necessarily be defined in ZFC. (ZF is Zermelo–Fraenkel set theory. ZFC is ZF with choice.) In ZF alone they cannot even be proved to exist. This was first established by Solovay [14] using an inaccessible cardinal. In the model of [14] no nonprincipal measure on ω is even ODR (definable from ordinal and real parameters). The HODR (hereditarily ODR) sets of this model form a model of ZF + DC (dependent choice) in which no nonprincipal measure on ω exists. Pincus [8] gave a model with the same properties making no use of an inaccessible. (This model was also known to Solovay.) The second model can be combined with ideas of A. Blass [1] to give a model of ZF + DC in which no nonprincipal measures exist on any set. Using this model one obtains a model of ZFC in which no nonprincipal measure on the set of real numbers is ODR. H. Friedman, in private communication, previously obtained such a model of ZFC by a different method. Our construction will be sketched in 4.1.

Terminology. PA is Peano Arithmetic, classical first-order arithmetic with induction. ⌈A⌉ is the formal numeral in PA for the Gödel number of A. – A is the negation of A, (A&B) is the conjunction of A and B, and Bew(x) is the usual provability predicate for PA. neg(x), conj(x, y), bicond(x, y), and bew(x) are terms of PA such that for all sentences A and B of PA ⊢PA, neg(˹A˺) = ˹−A˺ ⊢PA Conj(˹A˺, ˹B˺)= ˹(A&B)˺ ⊢PA bicond(˹A˺, ˹B˺)= ˹(A ↔ B)˺, and ⊢PA bew(˹A˺) = ˹Bew(˹A˺)˺. T is the sentence ‘0 = 0’ and Con is the usual sentence expressing the consistency of PA. If A (x) is any formula of PA, then a fixed point of A(x) is a sentence S such that ⊢PAS ↔ A(˹S˺). (It is well known that every formula of PA with one free variable has a fixed point.) The P-terms are defined inductively by: the variable x is a P-term; if t(x) and u(x) are P-terms, so are neg(t(x)), conj(t(x), u(x)), and bew(t(x)). A basic P-formula is a formula Bew(t(x)), where t(x) is a P-term; and a P-formula is a truth-functional combination of basic P-formulas. An F-sentence is a member of the smallest class that contains Con and contains −A, (A&B), and −Bew(˹−A˺) whenever it contains A and B. In [B] we gave a decision procedure for the class of true F-sentences.

−Bew(x), Bew(x), and Bew(neg(x)) are examples of P-formulas, and fixed points of these particular P-formulas have been studied by Gödel, Henkin [H] and Löb [L], and Jeroslow [J], respectively. In this note we show how to decide whether or not a fixed point of any given P-formula is provable in PA.

In this note we shall assume acquaintance with [T4] and the parts of [T1] which deal with intuitionistic arithmetic in all finite types. The bibliography just continues the bibliography of [T4].

The principal purpose of this note is the discussion of two models for intuitionistic finite type arithmetic with fan functional (HAω + MUC). The first model is needed to correct an oversight in the proof of Theorem 6 [T4, §5]: the model ECF+ as defined there cannot be shown to have the required properties in EL + QF-AC, the reason being that a change in the definition of W12 alone does not suffice—if one wishes to establish closure under the operations of HAω the definitions of W1σ for other σ have to be adopted as well. It is difficult to see how to do this directly in a uniform way — but we succeed via a detour, which is described in §2.

For a proper understanding, we should perhaps note already here that on the assumption of the fan theorem, ECF+ as defined in [T4] and the new model of this note coincide (since then the definition of W12 [T4, p. 594] is equivalent to the definition for W12 in the case of ECF); but in EL it is impossible to prove this (and under assumption of Church's thesis the two models differ).

Let κ denote a regular uncountable cardinal and NS the normal ideal of nonstationary subsets of κ. Our results concern the well-known open question whether NS fails to be κ+-saturated, i.e., are there κ+ stationary subsets of κ with pairwise intersections nonstationary? Our first observation is:

Theorem. NS isκ+-saturated iff for every normal ideal J on κ there is a stationary set A ⊆ κsuch that J = NS∣A = {X ⊆ κ: X ∩ A ∈ NS}.

Turning our attention to large cardinals, we extend the usual (weak) Mahlo hierarchy to define “greatly Mahlo” cardinals and obtain the following:

Theorem. If κ is greatly Mahlo then NS is notκ+-saturated.

Theorem. If κ is ordinal Π11-indescribable (e.g., weakly compact), ethereal (e.g., subtle), or carries aκ-saturated ideal, thenκis greatly Mahlo. Moreover, there is a stationary set of greatly Mahlo cardinals below any ordinal Π11-indescribable cardinal.

These methods apply to other normal ideals as well; e.g., the subtle ideal on an ineffable cardinal κ is not κ+-saturated.

Although this problem is still open, there are a few related results concerning (i) theories equiconsistent with NF and (ii) consistent fragments of NF. Concerning (i) we will discuss the following results

(1) Specker's result about the equiconsistency of NF with an extension of the theory of types [16],

(2) the equiconsistency of NF with fragments of NF containing NFU [2], [10],

and a new one about

(3) the equiconsistency of NF with an extension of Zermelo's set theory with the axiom of comprehension restricted to bounded formulas.

Concerning (ii) we will give a simplified proof and a generalization of (4) Jensen's result about the consistency of NFU [13].

Only a few words will be devoted to

(5) Grishin's results and refinements [4], [5], [8], [9], treated with more details in [4].

The reader who is unfamiliar with NF or who has a natural repulsion for this system is first invited to read the excellent account contained in [7, Chapter III, §3].

Let L be any finitary language. By restricting our attention to the universal Horn sentences of L and appealing to a semantical notion of logical consequence, we can formulate the universal Horn logic of L. The present paper provides some theorems about universal Horn logic that serve to distinguish it from the full first order predicate logic. Universal Horn equivalence between structures is characterized in two ways, one resembling Kochen's ultralimit theorem. A sharp version of Beth's definability theorem is established for universal Horn logic by means of a reduced product construction. The notion of a consistency property is relativized to universal Horn logic and the corresponding model existence theorem is proven. Using the model existence theorem another proof of the definability result is presented. The relativized consistency properties also suggest a syntactical notion of proof that lies entirely within the universal Horn logic. Finally, a decision problem in universal Horn logic is discussed. It is shown that the set of universal Horn sentences preserved under the formation of homomorphic images (or direct factors) is not recursive, provided the language has at least two unary function symbols or at least one function symbol of rank more than one.

This paper begins with a discussion of how algebraic relations between structures can be used to obtain fragments of a given logic. Only two such fragments seem to be under current investigation: equational logic and universal Horn logic. Other fragments which seem interesting are pointed out.

The comprehension principle of second order arithmetic asserts the existence of certain species (sets) corresponding to properties of natural numbers. In the intuitionistic theory of sequences of natural numbers there is an analoguous principle, implicit in Brouwer's writing and explicitly stated by Kripke, which asserts the existence of certain sequences corresponding to statements. The justification of this principle, Kripke's Schema, makes use of the concept of the so-called creative subject. For more information the reader is referred to Troelstra [5].

Kripke's Schema reads

There is a weaker version

The idea to reduce species to sequences via Kripke's schema occurred several years ago (cf. [2, p. 128], [5, p. 104]). In [1] the reduction technique was applied in the construction of a model for HAS.

On second thought, however, I realized that there is a straightforward, simpler way to exploit Kripke's schema, avoiding models altogether. The idea to present this material separately was forced on the author by C. Smorynski.

Consider a second order arithmetic with both species and sequence variables. By KS we have

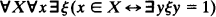
(for convenience we restrict ourselves in KS to 0-1-sequences). An application of AC-NF gives

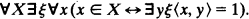
Of course ξ is not uniquely determined. This is the key to the reduction of full second order arithmetic, or HAS, to a theory of sequences.

We now introduce a translation τ to eliminate species variables. It is no restriction to suppose that the formulae contain only the sequence variables ξ1, ξ3, ξ5, …

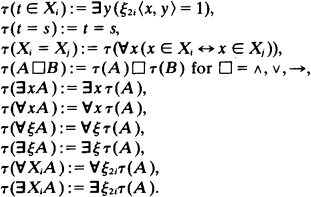
Note that by virtue of the definition of τ the axiom of extensionality is automatically verified after translation. The translation τ eliminates the species variables and leaves formulae without species variables invariant.

Ellerman, Comer, and Macintyre have all observed that sheaves are an interesting generalization of models and are deserving of model theoretic attention. Scott has pointed out that sheaves are Heyting algebra valued models. The reverse does not hold however since almost no genuine Boolean valued model is a sheaf.

In §1 we shall review the definition of a sheaf and prove a theorem about Boolean valued models using the sheaf construction. In §2 we shall be concerned with the set of sentences preserved by global sections. Our principal result is that global section sentences are also normal submodel sentences. (We define as a normal submodel of if is a submodel of and every point of B − A can be moved by an automorphism of which fixes each point of A.) In §3 we prove that every normal submodel sentence is the negation of a disjunction of Horn sentences and that the set of normal submodel sentences is r.e. but not recursive. §3 involves only traditional model theory and can be read independently of the first two sections.

The Löwenheim–Skolem theorem states that if a theory has an infinite model it has models of all cardinalities greater than or equal to the cardinality of the language in which the theory is defined. A natural question is what happens if there is a model whose cardinality is less than that of the language.

If κ is an infinite cardinal less than the first measurable cardinal and κ < κω, the Rabin–Keiler theorem [1, p. 139] gives an example of a theory which has a model of cardinality κ in which every element is the interpretation of a constant and all other models have cardinality μ ≥ κω. Keisler has also shown that if a theory has a model of cardinality κ it has models of all cardinalities μ ≥ κω. We will show that within the bounds of the above theorems anything can happen.

The main result is as follows.

A model is called minimal if it does not contain a proper elementary submodel. A class of models is called Σ11(Π11 resp. elementary) if it is axiomatized by a sentence with σ in and some string of predicate symbols. All languages considered are assumed to be countable. For each model we shall define in a natural way its rank, denoted by rk (), which is an ordinal or ∞. Intuitively speaking, rk () is the least upper bound for the number of steps needed to define the elements of by first order formulas; e.g. we shall have rk((ω, <)) = 1 (each element is f.o. definable), rk ((Z, <)) = 2 (no element is f.o. definable, each element is f.o. definable using any other element as a parameter), rk ((Q, <) ) = ∞ (no element is f.o. definable by any number of steps). This notion of rank leads to a useful game theoretic characterization of minimal models which we apply to show that the Π11 class of minimal models is not Σ11.

The language Ln is obtained from the first order predicate calculus by adjoining the quantifier Qn which binds n variables. The formula Qnυ1 … υnΨ is given a κ-interpretation for each infinite cardinal κ, namely, “there is a set X of power κ such that Ψx1 … xn holds for all distinct x1 … xn ϵ X”. L<ω is the result of adjoining all the Qn quantifiers for each n ϵ ω to the first order predicate calculus.

In [4] we showed that under the assumption (cf. [3]) L<ω is countably compact under the ω1-interpretation, and that any sentence σ ϵ L<ω that has a model in some κ-interpretation where κ is a regular infinite cardinal has a model in the ω1 interpretation. However, compactness for L<ω in the κ-interpretation for κ an infinite successor cardinal other than ω1 and the transfer of satisfiability from ω1 to any higher power remain open questions under any set theoretic assumptions.

Here we restrict our attention to a small fragment L2− of L2 consisting of universal first order formulas along with formulas of the kind Q2υ1υ2∀υ3 … υnΨ and ¬Q2υ1υ2∀υ3 … υnφ where Ψ and φ are open and no function symbol of arity > 1 occurs in any formula. Assuming the existence of a κ-Souslin tree, this language is λ compact in the κ-interpretation when λ < κ.

This is a continuation of two previous papers by the same title [2] and examines mainly the interpolation property for the logic CD with constant domains, i.e., the extension of the intuitionistic predicate logic with the schema

It is known [3], [4] that this logic is complete for the class of all Kripke structures with constant domains.

Theorem 47. The strong Robinson consistency theorem is not true for CD.

Proof. Consider the following Kripke structure with constant domains. The set S of possible worlds is ω0, the set of positive integers. R is the natural ordering ≤. Let ω0 0 = , Bn, is a sequence of pairwise disjoint infinite sets. Let L0 be a language with the unary predicates P, P1 and consider the following extensions for P,P1 at the world m.

(a) P is true on ⋃i≤2nBi, and P1 is true on ⋃i≤2n+1Bi for m = 2n.

(b) P is true on ⋃i≤2nBi, and P1 for ⋃i≤2n+1Bi for m = 2n.

Let (Δ,Θ) be the complete theory of this structure. Consider another unary predicate Q. Let L be the language with P, Q and let M be the language with P1, Q.

In [2] Galvin and Hajnal showed, as a corollary to a more general result, that if , is a strong limit cardinal, then . They established similar bounds for powers of singular cardinals of cofinality greater than ω. Jech and Prikry in [3] showed that the Galvin-Hajnal bound can be improved if we assume that ω1 carries an ω2 saturated ω1 complete, nontrivial ideal. (See [7] for definitions), namely: under the given assumption provided is a strong limit cardinal.

In this paper we show that the same conclusion can be derived from Chang's Conjecture (see below) which is, at least consistencywise, a weaker assumption than the existence of an ω2 saturated ideal on ω1. We do not know if assumptions like these are necessary for obtaining the result.

Our notations and terminology should be understood by any reader acquainted with set theory. Chang's Conjecture is the following model theoretic assumption introduced by C. C. Chang:

which is deciphered as follows: Every structure 〈A, R,…〉 in a countable type where ∣A∣ = ω2, R ⊆ A, ∣R∣ = ω1 has an elementary substructure: 〈A′,R′,…〉 where ∣A′∣ = ω1 and ∣R′∣ = ω0. The consistency of Chang's Conjecture modulo the existence of Ramsey cardinals is claimed in [5].

A variety V (equational class of algebras) satisfies a strong Malcev condition ∃f1,…, ∃fnθ(f1, …, fn, x1, …, xm) where θ is a conjunction of equations in the function variables f1, …, fn and the individual variables x1, …, xm, if there are polynomial symbols p1, …, pn in the language of V such that ∀x1, …, xmθ(p1 …, pn, x1, …, xm) is a law of V. Thus a strong Malcev condition involves restricted second order quantification of a strange sort. The quantification is restricted to functions which are “polynomially definable”. This notion was introduced by Malcev [6] who used it to describe those varieties all of whose members have permutable congruence relations. The general formal definition of Malcev conditions is due to Grätzer [1]. Since then and especially since Jónsson's [3] characterization of varieties with distributive congruences there has been extensive study of strong Malcev conditions and the related concepts: Malcev conditions and weak Malcev conditions.

In [9], Taylor gives necessary and sufficient semantic conditions for a class of varieties to be defined by a (strong) Malcev condition. A key to the proof is the translation of the restricted second order concepts into first order concepts in a certain many sorted language. In this paper we show that, given this translation, Taylor's theorem is an easy consequence of a result of Tarski [8] and the standard preservation theorems of first order logic.

The theorem introduced here provides a sufficient condition for an axiomatic class to be elementary. It resulted from consideration of a definability problem in , but is introduced in a less specific context and accompanied by applications to .

As in [La, 1], [La, 2], a reflexive, transitive binary relation R on a nonempty set S will be called a quasi-ordering or q.o. of S. A set of pairwise incomparable elements of S is an antichain and a subset of S linearly ordered by R is a chain. A chain {Si: i ∈ ω} with i > j if and only if (siRsj ∧ ¬ sjRSi) will be called an infinite descending chain. If S has no infinite antichains nor any infinite descending chains, S is well quasi-ordered by R, and is called a well quasi-ordering or w.q.o. Any subset of a w.q.o. is a w.q.o. An element s of a q.o. S is minimal in S if ∀t ∈ S(tRs → sRt). A subset S′ of S is a foundation for S if ∀t ∈ S∃s ∈ S′(sRt).

We consider first-order logic only. A theory S will be called locally interpretable in a theory T if every theorem of S is interpretable in T. If S is locally interpretable in T and T is consistent then S is consistent. Most known relative consistency proofs can be viewed as local interpretations. The classic examples are the cartesian interpretation of the elementary theorems of Euclidean n-dimensional geometry into the first-order theory of real closed fields, the interpretation of the arithmetic of integers (rational numbers) into the arithmetic of positive integers, the interpretation of ZF + (V = L) into ZF, the interpretation of analysis into ZFC, relative consistency proofs by forcing, etc. Those interpretations are global. Under fairly general conditions local interpretability implies global interpretability; see Remarks (7), (8), and (9) below.

We define the type (interpretability type) of a theory S to be the class of all theories T such that S is locally interpretable in T and vice versa. There happen to be such types and they are partially ordered by the relation of local interpretability. This partial ordering is of lattice type and has the following form:

The lattice is distributive and complete and satisfies the infinite distributivity law of Brouwerian lattices:

We do not know if the dual law

is true. We will show that the lattice is algebraic and that its compact elements form a sublattice and are precisely the types of finitely axiomatizable theories, and several other facts.

We use the notation of Kripke's paper [1]. Let M = (G, K, R) be a tree structure and D a domain and η a Beth model on M. The truth conditions of the Beth semantics for ∨ and ∃ are (see [1]):

(a) η (A ∨ B, H) = T iff for some B ⊆ K, B bars H and for each H′ ∈ B, either η(A, H′) = T or η(B, H′) = T.

(b) η(∃xA(x), H) = T iff for some B ⊆ K, B bars H and for each H′ ∈ B there exists an a ∈ D such that η(A (a), H′) = T.

Suppose we change the truth definition η to η* by replacing condition (b) by the condition (b*) (well known from the Kripke interpretation):

Call this type of interpretation the new version of Beth semantics. We prove

Theorem 1. Intuitionistic predicate logic is complete for the new version of the Beth semantics.

Since Beth structures are of constant domains, and in the new version of Beth semantics the truth conditions for ∧, →, ∃, ∀, ¬ are the same as for the Kripke interpretation, we get:

Corollary 2. The fragment without disjunction of the logic CD of constant domains (i.e. with the additional schema ∀x(A ∨ B(x))→ A ∨ ∀xB(x), x not free in A) equals the fragment without disjunction of intuitionistice logic.