Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-25T07:11:33.409Z Has data issue: false hasContentIssue false
  • English
  • Français

Sheaves and normal submodels

Published online by Cambridge University Press:  12 March 2014

Richard Mansfield
Richard Mansfield*
Affiliation:
Pennsylvania State University, University Park, PA 16802
Get access Rights & Permissions [Opens in a new window]

Extract

Ellerman, Comer, and Macintyre have all observed that sheaves are an interesting generalization of models and are deserving of model theoretic attention. Scott has pointed out that sheaves are Heyting algebra valued models. The reverse does not hold however since almost no genuine Boolean valued model is a sheaf.

In §1 we shall review the definition of a sheaf and prove a theorem about Boolean valued models using the sheaf construction. In §2 we shall be concerned with the set of sentences preserved by global sections. Our principal result is that global section sentences are also normal submodel sentences. (We define 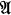as a normal submodel o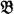f if 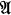is a submodel of 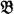and every point of B − A can be moved by an automorphism of 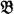which fixes each point of A.) In §3 we prove that every normal submodel sentence is the negation of a disjunction of Horn sentences and that the set of normal submodel sentences is r.e. but not recursive. §3 involves only traditional model theory and can be read independently of the first two sections.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 42 , Issue 2 , June 1977 , pp. 241 - 250
Copyright
Copyright © Association for Symbolic Logic 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[0]Baldwin, J. T. and Lachlan, A. H., On universal Horn sentences categorical in some infinite powers.Google Scholar
[1]Chang, C. C. and Keisler, H. J., Model theory, North-Holland, Amsterdam, 1973.Google Scholar
[2]Comer, S. H., Elementary properties of structures.Google Scholar
[3]Comer, S. H., Representations of algebras by sections over Boolean spaces, Pacific Journal of Mathematics, vol. 38 (1971), pp. 29–38.CrossRefGoogle Scholar
[4]Ellerman, D. P., Sheaves of structures and generalized ultraproducts, Annals of Mathematical Logic, vol. 7 (1974), pp. 163–195.Google Scholar
[5]Feferman, S. and Vaught, R. L., The first order properties of algebraic systems, Fundamente Mathematicae, vol. 47 (1959), pp. 57–103.CrossRefGoogle Scholar
[6]Galvin, F., Horn sentences, Annals of Mathematical Logic, vol. 1 (1970), pp. 389–422.Google Scholar
[7]Macintyre, A., Model completeness for sheaves of structures, Fundamenta Mathematicae, vol. 81 (1973), pp. 73–89.CrossRefGoogle Scholar
[8]Mansfield, R., The theory of Boolean ultrapowers, Annals of Mathematical Logic, vol. 2 (1974), pp. 163–195.Google Scholar
[9]Mansfield, R., Horn sentences and reduced direct products, Transactions of the American Mathematical Society, vol. 172 (1972) pp. 279–286.CrossRefGoogle Scholar
[10]Volger, H., The Feferman-Vaught theorem revisited, Tübingen, 1973 (preprint).Google Scholar