Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-22T20:39:28.660Z Has data issue: false hasContentIssue false
  • English
  • Français

Chang's conjecture and powers of singular cardinals

Published online by Cambridge University Press:  12 March 2014

Menachem Magidor
Menachem Magidor*
Affiliation:
Ben Ourion University of the Negev, Beersheva, Israel
Get access Rights & Permissions [Opens in a new window]

Extract

In [2] Galvin and Hajnal showed, as a corollary to a more general result, that if 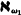, is a strong limit cardinal, then 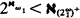. They established similar bounds for powers of singular cardinals of cofinality greater than ω. Jech and Prikry in [3] showed that the Galvin-Hajnal bound can be improved if we assume that ω1 carries an ω2 saturated ω1 complete, nontrivial ideal. (See [7] for definitions), namely: under the given assumption 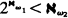provided 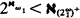is a strong limit cardinal.

In this paper we show that the same conclusion can be derived from Chang's Conjecture (see below) which is, at least consistencywise, a weaker assumption than the existence of an ω2 saturated ideal on ω1. We do not know if assumptions like these are necessary for obtaining the result.

Our notations and terminology should be understood by any reader acquainted with set theory. Chang's Conjecture is the following model theoretic assumption introduced by C. C. Chang:

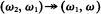
which is deciphered as follows: Every structure 〈A, R,…〉 in a countable type where ∣A∣ = ω2, R ⊆ A, ∣R∣ = ω1 has an elementary substructure: 〈A′,R′,…〉 where ∣A′∣ = ω1 and ∣R′∣ = ω0. The consistency of Chang's Conjecture modulo the existence of Ramsey cardinals is claimed in [5].

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 42 , Issue 2 , June 1977 , pp. 272 - 276
Copyright
Copyright © Association for Symbolic Logic 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Fodor, G., Stationary subsets and regressive functions, Acta Scientiarum Mathematicarum, (Szeged), vol. 27 (1966), pp. 105–110.Google Scholar
[2]Galvin, F. and Hajnal, A., Inequalities for cardinal powers, Annals of Mathematics, vol. 101 (1975), pp. 491–498.CrossRefGoogle Scholar
[3]Jech, T. and Prikry, K., On ideals of sets and the power set operation (to appear).Google Scholar
[4]Shidenfield, J., Unramified forcing, Axiomatic set theory, Proceedings of Symposia in Pure Mathematics, vol. 13 (1971), Providence, R.I., pp. 351–382.Google Scholar
[5]Silver, J., The dependence of Kurepa Conjecture and two Cardinal's Conjectures in model theory, Axiomatic set theory, Proceedings of Symposia in Pure Mathematics, vol. 13 (1971), Providence, R.I., pp. 383–390.Google Scholar
[6]Silver, J., On the singular cardinals problem, Proceedings of the International Congress of Mathematics, Vancouver, 1974, Vol. I, pp. 265–268.Google Scholar
[7]Solsvay, R. M., Real valued measurable cardinals, Axiomatic set theory, Proceedings of Symposia in Pure Mathematics, vol. 13 (1971), Providence, R.I., pp. 397–428.Google Scholar