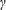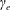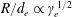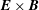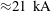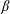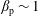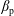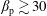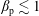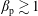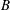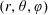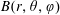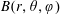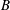The confinement of the guiding-centre trajectories in a stellarator is determined by the variation of the magnetic field strength 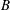 $B$ in Boozer coordinates
$B$ in Boozer coordinates 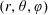 $(r,\unicode[STIX]{x1D703},\unicode[STIX]{x1D711})$, but
$(r,\unicode[STIX]{x1D703},\unicode[STIX]{x1D711})$, but 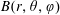 $B(r,\unicode[STIX]{x1D703},\unicode[STIX]{x1D711})$ depends on the flux surface shape in a complicated way. Here we derive equations relating
$B(r,\unicode[STIX]{x1D703},\unicode[STIX]{x1D711})$ depends on the flux surface shape in a complicated way. Here we derive equations relating 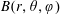 $B(r,\unicode[STIX]{x1D703},\unicode[STIX]{x1D711})$ in Boozer coordinates and the rotational transform to the shape of flux surfaces in cylindrical coordinates, using an expansion in distance from the magnetic axis. A related expansion was done by Garren and Boozer (Phys. Fluids B, vol. 3, 1991a, 2805) based on the Frenet–Serret frame, which can be discontinuous anywhere the magnetic axis is straight, a situation that occurs in the interesting case of omnigenity with poloidally closed
$B(r,\unicode[STIX]{x1D703},\unicode[STIX]{x1D711})$ in Boozer coordinates and the rotational transform to the shape of flux surfaces in cylindrical coordinates, using an expansion in distance from the magnetic axis. A related expansion was done by Garren and Boozer (Phys. Fluids B, vol. 3, 1991a, 2805) based on the Frenet–Serret frame, which can be discontinuous anywhere the magnetic axis is straight, a situation that occurs in the interesting case of omnigenity with poloidally closed 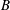 $B$ contours. Our calculation in contrast does not use the Frenet–Serret frame. The transformation between the Garren–Boozer approach and cylindrical coordinates is derived, and the two approaches are shown to be equivalent if the axis curvature does not vanish. The expressions derived here help enable optimized plasma shapes to be constructed that can be provided as input to VMEC and other stellarator codes, or to generate initial configurations for conventional stellarator optimization.
$B$ contours. Our calculation in contrast does not use the Frenet–Serret frame. The transformation between the Garren–Boozer approach and cylindrical coordinates is derived, and the two approaches are shown to be equivalent if the axis curvature does not vanish. The expressions derived here help enable optimized plasma shapes to be constructed that can be provided as input to VMEC and other stellarator codes, or to generate initial configurations for conventional stellarator optimization.
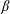 $\unicode[STIX]{x1D6FD}$ plasmas
$\unicode[STIX]{x1D6FD}$ plasmas