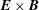1 Introduction
Dusty plasmas are plasmas containing solid, charged particles of micron to sub-micron size. Typically in low temperature plasmas, where the dominant charging process is the collection of electrons and ions, the dust is negatively charged owing to the higher mobility of the electrons. The physics of dusty plasmas has application to a wide range of space and astrophysical environments as well as various laboratory plasmas. In many of these environments, the plasma is immersed in a magnetic field. While most laboratory experiments on dusty plasmas have been performed without magnetic fields, there have been a number of experimental investigations on the dynamics of the dust in magnetized plasmas (e.g. Konopka et al. Reference Konopka, Samsonov, Ivlev, Goree, Steinberg and Morfill2000; Kaw et al. Reference Kaw, Nishikawa and Sato2002; Samsonov et al. Reference Samsonov, Zhdanov, Morfill and Steinberg2003; Schulze et al. Reference Schulze, O’Connell, Gans, Awakowicz and von Keudell2007; D’yachkov, Petrov & Fortov Reference D’yachkov, Petrov and Fortov2009; Karasev et al. Reference Karasev, Dzlieva, Eikhval’d, Ermolenko, Golubev and Ivanov2009). More recently, new dusty plasma devices with high magnetic field have been developed, such as the Magnetized Dusty Plasma Experiment (MDPX) at Auburn University, designed to investigate the properties of a dusty plasma under conditions where some or all of the charged particle species are magnetized (Thomas, Merlino & Rosenberg Reference Thomas, Merlino and Rosenberg2012).
In a device such as MDPX, there can be a component of electric field
$\boldsymbol{E}$
perpendicular to the magnetic field
$\boldsymbol{B}$
, which, for example, electrostatically confines the dust (see Thomas et al.
Reference Thomas, Dubois, Lynch, Adams, Fisher, Artis, LeBlanc, Konopka, Merlino and Rosenberg2014). Motivated by this, we consider a possible instability that may occur under conditions where the ions (and electrons) are magnetized and acquire
$\boldsymbol{E}\times \boldsymbol{B}$
drifts relative to the dust which is unmagnetized. In this case, theories have shown that an ion
$\boldsymbol{E}\times \boldsymbol{B}$
drift,
$U_{\bot }$
, could excite low frequency dust-acoustic-type waves (e.g. Shukla, Salimullah & Sorasio Reference Shukla, Salimullah and Sorasio2002; D’Angelo Reference D’Angelo2003; Rosenberg & Shukla Reference Rosenberg and Shukla2007; Rosenberg Reference Rosenberg2014). In this paper we focus on a particular type of ion cross-field drift driven instability, namely, a beam-cyclotron-type instability for purely perpendicular propagation (Rosenberg Reference Rosenberg2014). This instability excites a spectrum of dust waves at quasi-discrete wavenumbers where roughly
$k_{\bot }U_{\bot }\sim m\unicode[STIX]{x1D714}_{ci}$
, where
$k_{\bot }$
is the perpendicular wavenumber,
$m$
is an integer and
$\unicode[STIX]{x1D714}_{ci}$
is the positive ion gyrofrequency. The instability is a low frequency analogue of the ‘standard’ beam-cyclotron instability in a plasma containing magnetized electrons and unmagnetized ions (e.g. Gary & Sanderson Reference Gary and Sanderson1970; Lampe et al.
Reference Lampe, Manheimer, McBride, Orens, Shanny and Sudan1971, Reference Lampe, Manheimer, McBride, Orens, Papadopoulos, Shanny and Sudan1972). In the standard beam-cyclotron instability, an electron
$\boldsymbol{E}\times \boldsymbol{B}$
drift excites ion waves at discrete wavenumbers where
$k_{\bot }U_{\bot }\sim m\unicode[STIX]{x1D714}_{ce}$
, where
$\unicode[STIX]{x1D714}_{ce}$
is the electron gyrofrequency. The standard beam-cyclotron instability has relevance to Hall thrusters, where the instability has been referred to as a high frequency or
$\boldsymbol{E}\times \boldsymbol{B}$
electron drift instability (e.g. Adam, Heron & Laval Reference Adam, Heron and Laval2004; Ducrocq et al.
Reference Ducrocq, Adam, Heron and Laval2006; Cavalier et al.
Reference Cavalier, Lemoine, Tsikata, Honoré, Grésillon and Bonhomme2011, Reference Cavalier, Lemoine, Bonhomme, Tsikata, Honore and Gresillon2013; Boeuf Reference Boeuf2017). For the low frequency analogue instability in a dusty plasma, where the ion
$\boldsymbol{E}\times \boldsymbol{B}$
drift excites dust waves at quasi-discrete wavenumbers, collisional effects are generally significant and can affect the linear growth rates and nonlinear development of the instability.
Section 2 discusses the dispersion relation for the linear instability, and our set of reduced parameters for the numerical simulations. Section 3 gives the simulation approach and presents the results of the numerical simulations. Most of this section focuses on simulations in a collisional plasma, but a brief comparison with the collisionless case is also discussed. Section 4 gives a summary and discussion.
2 Dispersion relation and parameters
2.1 Linear dispersion relation
The model plasma is composed of singly charged positive ions, negatively charged dust of uniform radius
$R$
(thus uniform mass and charge) and neutrals. The condition of equilibrium charge neutrality is
$n_{i}=n_{e}+Z_{d}n_{d}$
, where
$n_{\unicode[STIX]{x1D6FC}}$
is the number density of species
$\unicode[STIX]{x1D6FC}$
, with the subscripts
$i,e,d$
and
$n$
referring to ions, electrons, dust and neutrals, respectively, and
$Z_{d}$
is the charge state of the dust.
We consider a slab geometry, with an external magnetic field
$\boldsymbol{B}$
in the
$\boldsymbol{z}$
direction, and an electric field
$\boldsymbol{E}$
in the
$\boldsymbol{y}$
direction. The ions and electrons are magnetized and have an
$\boldsymbol{E}\times \boldsymbol{B}$
drift,
$\boldsymbol{U}_{\bot }=(cE/B)\boldsymbol{x}$
. This is the laboratory frame that will be used for the simulations. It is assumed that the dust collision frequency is much larger than the dust gyrofrequency so that the dust grains are unmagnetized. We will assume that the ratio of the ion plasma frequency to the ion gyrofrequency is somewhat greater than one.
To obtain an analytic expression for the growth rate for the dust beam-cyclotron instability, we consider the reference frame where the ions and electrons are stationary and the dust moves in the
$x$
-direction with speed
$U_{\bot }$
. In this frame, one can view the instability as a dust beam exciting ion Bernstein waves with frequencies near harmonics of the ion gyrofrequency
$\unicode[STIX]{x1D714}_{ci}$
. (Note that in the laboratory or simulation frame, the ion drift excites dust waves; the ion Bernstein waves are Doppler shifted to low frequency by the ion drift and can couple to dust-acoustic-type waves.) We use Maxwellians for the electron and ion distribution functions and a shifted Maxwellian for the dust, and model collisions roughly using a number conserving Krook collision term (see e.g. Opher, Morales & Leboeuf Reference Opher, Morales and LeBoeuf2002). Then the linear dispersion relation for electrostatic waves with wavevector
$\boldsymbol{k}=(k_{x},0,k_{z})$
is given by (e.g. Kindel & Kennel Reference Kindel and Kennel1971; Ossakow et al.
Reference Ossakow, Papadopoulos, Orens and Coffey1975; Alexandrov, Bogdankevich & Rukhadze Reference Alexandrov, Bogdankevich and Rukhadze1984; Rosenberg Reference Rosenberg2010)
$$\begin{eqnarray}1+\unicode[STIX]{x1D712}_{e}+\unicode[STIX]{x1D712}_{i}+\unicode[STIX]{x1D712}_{d}=0,\end{eqnarray}$$
where
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D712}_{j}=\frac{1}{k^{2}\unicode[STIX]{x1D706}_{Dj}^{2}}\left[1+\mathop{\sum }_{s=-\infty }^{+\infty }\unicode[STIX]{x1D701}_{j,0}Z(\unicode[STIX]{x1D701}_{j,s})\unicode[STIX]{x1D6E4}_{s}(b_{j})\right]\left[1+\mathop{\sum }_{s=-\infty }^{+\infty }\frac{\text{i}\unicode[STIX]{x1D708}_{j}}{\sqrt{2}k_{z}v_{j}}\unicode[STIX]{x1D6E4}_{s}(b_{j})Z(\unicode[STIX]{x1D701}_{j,s})\right]^{-1}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D712}_{d}=\frac{1}{k^{2}\unicode[STIX]{x1D706}_{Dd}^{2}}[1+\unicode[STIX]{x1D701}_{d}Z(\unicode[STIX]{x1D701}_{d})]\left[1+\frac{\text{i}\unicode[STIX]{x1D708}_{d}}{\sqrt{2}kv_{d}}Z(\unicode[STIX]{x1D701}_{d})\right]^{-1}. & \displaystyle\end{eqnarray}$$
$\unicode[STIX]{x1D706}_{D\unicode[STIX]{x1D6FC}}=(T_{j}/4\unicode[STIX]{x03C0}n_{\unicode[STIX]{x1D6FC}}Z_{\unicode[STIX]{x1D6FC}}^{2}\text{e}^{2})^{1/2}$
is the Debye length of species
$\unicode[STIX]{x1D6FC}$
,
$Z$
is the plasma dispersion function (Fried & Conte Reference Fried and Conte1961), the subscript
$j=e,i$
and 
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D701}_{j,s}=\frac{\unicode[STIX]{x1D714}+\text{i}\unicode[STIX]{x1D708}_{j}-s\unicode[STIX]{x1D714}_{cj}}{\sqrt{2}k_{z}v_{j}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D701}_{d}=\frac{\unicode[STIX]{x1D714}-k_{x}U_{\bot }+\text{i}\unicode[STIX]{x1D708}_{d}}{\sqrt{2}kv_{d}}. & \displaystyle\end{eqnarray}$$
$v_{\unicode[STIX]{x1D6FC}}=(T_{\unicode[STIX]{x1D6FC}}/m_{\unicode[STIX]{x1D6FC}})^{1/2}$
is the thermal speed,
$\unicode[STIX]{x1D70C}_{j}=v_{j}/\unicode[STIX]{x1D714}_{cj}$
is the gyroradius of particle species
$j$
,
$b_{j}=k_{x}^{2}\unicode[STIX]{x1D70C}_{j}^{2}$
, and
$\unicode[STIX]{x1D6E4}_{s}(b_{j})=\text{I}_{s}(b_{j})\exp (-b_{j})$
, with
$\text{I}_{s}$
the modified Bessel function of order
$s$
, and
$\unicode[STIX]{x1D708}_{\unicode[STIX]{x1D6FC}}$
denotes the collision rates of charged particles with neutrals. In the following we consider perpendicular propagation with
$k_{z}=0$
. Therefore,
$k=k_{x}$
. Because
$\unicode[STIX]{x1D714}\ll \unicode[STIX]{x1D714}_{ce}$
, we retain only the zeroth-order harmonic for the electrons. With
$b_{e}\ll 1$
, the electron susceptibility becomes
$$\begin{eqnarray}\unicode[STIX]{x1D712}_{e}=\frac{\unicode[STIX]{x1D714}_{pe}^{2}}{\unicode[STIX]{x1D714}_{ce}^{2}}\left(1+\frac{\text{i}\unicode[STIX]{x1D708}_{e}}{\unicode[STIX]{x1D714}}\right).\end{eqnarray}$$
Because we are considering parameters where
$\unicode[STIX]{x1D714}_{pi}/\unicode[STIX]{x1D714}_{ci}$
is of the order of a few, we neglect
$\unicode[STIX]{x1D712}_{e}$
in the following, which is reasonable as long as
$\unicode[STIX]{x1D708}_{e}/\unicode[STIX]{x1D714}_{ce}\ll (\unicode[STIX]{x1D714}_{ci}/\unicode[STIX]{x1D714}_{pi})^{2}(n_{i}/n_{e})$
, which would generally be satisfied in order for the electrons to be magnetized.
The ion susceptibility is
$$\begin{eqnarray}\unicode[STIX]{x1D712}_{i}=\frac{1}{k^{2}\unicode[STIX]{x1D706}_{Di}^{2}}\left[1-\unicode[STIX]{x1D6E4}_{0}(b_{i})-\mathop{\sum }_{s=1}^{\infty }\frac{2\bar{\unicode[STIX]{x1D714}}^{2}\unicode[STIX]{x1D6E4}_{s}(b_{i})}{\bar{\unicode[STIX]{x1D714}}^{2}-s^{2}}\right]\left[1-\frac{\text{i}\unicode[STIX]{x1D708}_{i}\unicode[STIX]{x1D6E4}_{0}(b_{i})}{\bar{\unicode[STIX]{x1D714}}}-\mathop{\sum }_{s=1}^{\infty }\frac{2\bar{\unicode[STIX]{x1D714}}\text{i}\unicode[STIX]{x1D708}_{i}\unicode[STIX]{x1D6E4}_{s}(b_{i})}{\bar{\unicode[STIX]{x1D714}}^{2}-s^{2}}\right]^{-1}.\end{eqnarray}$$
Here
$\bar{\unicode[STIX]{x1D714}}=(\unicode[STIX]{x1D714}+\text{i}\unicode[STIX]{x1D708}_{i})/\unicode[STIX]{x1D714}_{ci}$
. In the limit that
$k\unicode[STIX]{x1D70C}_{i}>1$
, we take
$\unicode[STIX]{x1D6E4}_{s}(b_{i})\sim 1/\sqrt{2\unicode[STIX]{x03C0}b_{i}}$
as a rough approximation. Using the following sum identity for the cotangent (Gradshteyn & Ryzhik Reference Gradshteyn and Ryzhik1980):
$$\begin{eqnarray}\unicode[STIX]{x03C0}\cot (\unicode[STIX]{x03C0}z)=\frac{1}{z}+2z\mathop{\sum }_{s=1}^{\infty }\frac{1}{z^{2}-s^{2}},\end{eqnarray}$$
we approximate (2.5) as
$$\begin{eqnarray}\unicode[STIX]{x1D712}_{i}\approx \frac{1}{k^{2}\unicode[STIX]{x1D706}_{Di}^{2}}\left[1-\frac{\unicode[STIX]{x03C0}\bar{\unicode[STIX]{x1D714}}\cot (\unicode[STIX]{x03C0}\bar{\unicode[STIX]{x1D714}})}{\sqrt{2\unicode[STIX]{x03C0}b_{i}}}\right]\left[1-\frac{\unicode[STIX]{x03C0}i\bar{\unicode[STIX]{x1D708}_{i}}\cot (\unicode[STIX]{x03C0}\bar{\unicode[STIX]{x1D714}})}{\sqrt{2\unicode[STIX]{x03C0}b_{i}}}\right]^{-1}.\end{eqnarray}$$
Here
$\bar{\unicode[STIX]{x1D708}_{i}}=\unicode[STIX]{x1D708}_{i}/\unicode[STIX]{x1D714}_{ci}$
is the inverse of the ion Hall parameter. (See also Wong (Reference Wong1970) and Lampe et al. (Reference Lampe, Manheimer, McBride, Orens, Papadopoulos, Shanny and Sudan1972) for the magnetized electron susceptibility in an analysis of the beam-cyclotron instability in a collisionless electron-ion plasma.)
For cold dust, the dust susceptibility is
$$\begin{eqnarray}\unicode[STIX]{x1D712}_{d}=-\frac{\unicode[STIX]{x1D714}_{pd}^{2}}{(\unicode[STIX]{x1D714}-kU_{\bot })(\unicode[STIX]{x1D714}-kU_{\bot }+\text{i}\unicode[STIX]{x1D708}_{d})}.\end{eqnarray}$$
We neglect dust collisions in the following analysis, assuming
$\unicode[STIX]{x1D708}_{d}$
is much smaller than the maximum growth rate of the instability.
A resonance occurs when the real frequency
$\unicode[STIX]{x1D714}_{r}\sim m\unicode[STIX]{x1D714}_{ci}$
and the Doppler-shifted frequency,
$|\unicode[STIX]{x1D714}_{r}-kU_{\bot }|$
, is in the dust-acoustic frequency regime, and leads to enhanced growth of dust waves with a growth rate
$\unicode[STIX]{x1D6FE}$
. We take
$\bar{\unicode[STIX]{x1D714}}\sim m+\text{i}\bar{\unicode[STIX]{x1D708}_{i}}+\text{i}\bar{\unicode[STIX]{x1D6FE}}$
, where
$\bar{\unicode[STIX]{x1D6FE}}=\unicode[STIX]{x1D6FE}/\unicode[STIX]{x1D714}_{ci}$
. Assuming
$(\bar{\unicode[STIX]{x1D708}}_{i}+\bar{\unicode[STIX]{x1D6FE}})\unicode[STIX]{x03C0}<1$
, the ion susceptibility becomes very roughly
$$\begin{eqnarray}\unicode[STIX]{x1D712}_{i}\approx \frac{1}{k^{2}\unicode[STIX]{x1D706}_{Di}^{2}}\left[1+\frac{1}{\sqrt{2\unicode[STIX]{x03C0}b_{i}}}\frac{\text{i}m(\bar{\unicode[STIX]{x1D708}_{i}}+\bar{\unicode[STIX]{x1D6FE}})}{(\bar{\unicode[STIX]{x1D708}_{i}}+\bar{\unicode[STIX]{x1D6FE}})^{2}}\right].\end{eqnarray}$$
For a collisional dusty plasma, typically
$\unicode[STIX]{x1D708}_{i}\gg \unicode[STIX]{x1D6FE}$
since growth rates are in the dust plasma frequency range. Using (2.8) and (2.9) in (2.1) yields the approximate dispersion relation
$$\begin{eqnarray}1-\frac{\unicode[STIX]{x1D714}_{pd}^{2}}{(\unicode[STIX]{x1D714}-kU_{\bot })^{2}}+\frac{1}{k^{2}\unicode[STIX]{x1D706}_{Di}^{2}}\left[1+\frac{\text{i}m}{\sqrt{2\unicode[STIX]{x03C0}b_{i}}\bar{\unicode[STIX]{x1D708}_{i}}}\right]\approx 0.\end{eqnarray}$$
Taking
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{r}+\text{i}\unicode[STIX]{x1D6FE}$
, with
$\unicode[STIX]{x1D6FE}<|\unicode[STIX]{x1D714}_{r}-kU_{\bot }|$
yields roughly
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D714}_{r}-kU_{\bot }\approx -\frac{\unicode[STIX]{x1D714}_{pd}k\unicode[STIX]{x1D706}_{Di}}{(1+k^{2}\unicode[STIX]{x1D706}_{Di}^{2})^{1/2}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FE}\approx \frac{m\unicode[STIX]{x1D714}_{ci}}{\unicode[STIX]{x1D708}_{i}}\frac{1}{\sqrt{8\unicode[STIX]{x03C0}b_{i}}}\frac{\unicode[STIX]{x1D714}_{pd}k\unicode[STIX]{x1D706}_{Di}}{(1+k^{2}\unicode[STIX]{x1D706}_{Di}^{2})^{3/2}}. & \displaystyle\end{eqnarray}$$
The dispersion relation (2.1) admits a Hall-current-type instability in the long wavelength limit where
$b_{i}\ll 1$
and
$\unicode[STIX]{x1D714}_{r}\sim kU_{\bot }\ll \unicode[STIX]{x1D714}_{ci}$
. In this case, the ion susceptibility has the form of (2.4) with the replacement of the subscripts
$e\rightarrow i$
. Thus the dispersion relation, again assuming cold dust, becomes approximately
$$\begin{eqnarray}1+\frac{\unicode[STIX]{x1D714}_{pi}^{2}}{\unicode[STIX]{x1D714}_{ci}^{2}}\left(1+\frac{\text{i}\unicode[STIX]{x1D708}_{i}}{\unicode[STIX]{x1D714}}\right)-\frac{\unicode[STIX]{x1D714}_{pd}^{2}}{(\unicode[STIX]{x1D714}-kU_{\bot })^{2}}\approx 0.\end{eqnarray}$$
In the limit that
$(\unicode[STIX]{x1D714}_{pi}/\unicode[STIX]{x1D714}_{ci})^{2}\gg 1$
, this yields for the Doppler-shifted frequency and growth rate (see also Rosenberg Reference Rosenberg2016):
$$\begin{eqnarray}\displaystyle & \displaystyle |\unicode[STIX]{x1D714}_{r}-kU_{\bot }|\sim \unicode[STIX]{x1D714}_{pd}\frac{\unicode[STIX]{x1D714}_{ci}}{\unicode[STIX]{x1D714}_{pi}}\left(\frac{\sqrt{1+C^{2}}+1}{2(1+C^{2})}\right)^{1/2}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FE}\sim |\unicode[STIX]{x1D714}_{r}-kU_{\bot }|\left(\frac{\sqrt{1+C^{2}}-1}{\sqrt{1+C^{2}}+1}\right)^{1/2}, & \displaystyle\end{eqnarray}$$
$C=\unicode[STIX]{x1D708}_{i}/kU_{\bot }$
. Including the dust collision rate reduces the growth rate in (2.13b
) by a factor of approximately
$\unicode[STIX]{x1D708}_{d}/2$
.2.2 Parameters
We consider a set of nominal parameters which may be possible in MDPX shown in table 1 for an argon plasma containing dust of uniform radius
$R$
. Here,
$P$
is the argon gas pressure,
$n_{\unicode[STIX]{x1D6FC}},m_{\unicode[STIX]{x1D6FC}},T_{\unicode[STIX]{x1D6FC}},\unicode[STIX]{x1D706}_{D\unicode[STIX]{x1D6FC}}$
and
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6FC}}$
are the density, mass, temperature, Debye length and gyroradius of species
$\unicode[STIX]{x1D6FC}$
, with
$\unicode[STIX]{x1D6FC}=e,i,d$
corresponding to electrons, ions and negatively charged dust, respectively,
$Z_{d}$
is the dust charge state and
$m_{p}$
is the proton mass. With these parameters, the ratio of the ion plasma frequency to the ion gyrofrequency is
$\unicode[STIX]{x1D6FD}_{i}=\unicode[STIX]{x1D714}_{pi}/\unicode[STIX]{x1D714}_{ci}\sim 2/B_{T}$
where
$B_{T}$
is the magnetic field strength in units of 1 T. Taking the ion collision rate with neutrals to be
$\unicode[STIX]{x1D708}_{i}\sim \unicode[STIX]{x1D70E}_{in}n_{n}v_{i}$
, where
$n_{n}$
is the neutral density,
$v_{i}=(T_{i}/m_{i})^{1/2}$
and
$\unicode[STIX]{x1D70E}_{in}\sim 5\times 10^{-15}$
cm
$^{2}$
, we have that
$\unicode[STIX]{x1D708}_{i}/\unicode[STIX]{x1D714}_{pi}\sim 0.05$
. Then the ion Hall parameter,
$H_{i}\sim 10B_{T}$
. With
$B=0.5T$
,
$H_{i}\sim 5$
, so the ions are magnetized and the electrons are strongly magnetized. On the other hand, the dust would be unmagnetized. Taking the dust–neutral collision rate to be
$\unicode[STIX]{x1D708}_{d}\sim (4\sqrt{8\unicode[STIX]{x03C0}}/3)R^{2}n_{n}v_{n}(m_{n}/m_{d})\sim 240$
s
$^{-1}$
, we find this is much larger than the dust gyrofrequency
$\unicode[STIX]{x1D714}_{cd}\sim 3.8~\text{rad}~\text{s}^{-1}$
. The dust is also ‘warm’, in the sense that the ratio of the dust-acoustic speed,
$c_{d}=\unicode[STIX]{x1D706}_{Di}\unicode[STIX]{x1D714}_{pd}$
to the dust thermal speed
$v_{d}=(T_{d}/m_{d})^{1/2}$
,
$c_{d}/v_{d}\sim \sqrt{10}$
, is not
$\gg 1$
. We will consider the case where the perpendicular ion drift
$U_{\bot i}$
, which is due to an
$E\times B$
drift, is equal to the ion thermal speed
$v_{i}$
. For the above parameters, this implies that the electric field perpendicular to
$B$
is approximately
$E_{\bot }\sim 1.3~\text{V}~\text{cm}^{-1}$
, which appears reasonable for a low temperature rf or dc dusty plasma.
Table 1. ‘Nominal’ parameters.
Because it is time consuming to run a simulation with the possible laboratory parameters shown in table 1, we consider whether we can model the linearly unstable spectrum with a ‘reduced’ set of dimensionless parameters. These are given in table 2, along with the dimensionless parameters corresponding to the ‘nominal’ parameters in table 1. Here
$\unicode[STIX]{x1D703}$
is the angle between
$\boldsymbol{k}$
and
$\boldsymbol{B}$
, which is
$90^{\circ }$
for purely perpendicular propagation. For both the nominal and reduced parameters, we have that
$Z_{d}n_{d}/n_{i}=0.4$
; in addition the ratio of the dust-acoustic speed to the dust thermal speed,
$c_{d}/v_{d}\sim \unicode[STIX]{x1D714}_{pd}\unicode[STIX]{x1D706}_{Di}/v_{d}\approx \sqrt{10}$
. The normalized ion and dust collision rates, and the ion Hall parameter
$H_{i}=\unicode[STIX]{x1D714}_{ci}/\unicode[STIX]{x1D708}_{i}=5$
are the same for both parameter sets. The ratio
$\unicode[STIX]{x1D714}_{pd}/\unicode[STIX]{x1D714}_{pi}\ll 1$
for both sets of parameters, and the ordering
$\unicode[STIX]{x1D714}_{pd}\ll \unicode[STIX]{x1D708}_{i}\ll \unicode[STIX]{x1D714}_{pi}$
holds for both sets as well.
Table 2. Dimensionless parameters.
Figure 1 shows the solution of (2.1) for both sets of dimensionless parameters in table 2 in the frame where the dust is stationary and the ions have an
$E\times B$
drift,
$U_{\bot i}=v_{i}$
. The solid curves correspond to the nominal parameters, while the dotted curves correspond to the reduced parameters. (For the nominal parameters, the electrons have an
$E\times B$
drift,
$U_{\bot e}=1.04v_{i}$
and collisions with neutrals are included with a rate
$\unicode[STIX]{x1D708}_{e}/\unicode[STIX]{x1D714}_{pi}=14$
. For the reduced parameters, the electrons have
$U_{\bot e}=0$
and
$\unicode[STIX]{x1D708}_{e}=0$
. The electron susceptibility is basically negligible, since for purely propagation it is proportional to
$\unicode[STIX]{x1D714}_{pe}^{2}/\unicode[STIX]{x1D714}_{ce}^{2}$
which is
${<}10^{-2}$
for both sets of parameters.) The peaks in the growth rate at wavenumbers satisfying the resonance condition
$kU_{\bot ,i}\sim m\unicode[STIX]{x1D714}_{ci}$
correspond to the dust beam-cyclotron instability, while the much smaller peak at small
$k$
corresponds to the Hall-current instability. It should be noted that ion collisional effects lead to a broadening of the peaks in the growth rate of the beam-cyclotron instability, and a reduction in the magnitude of the growth rate (see (2.11b
)). On the other hand, the growth rate of the Hall-current instability (2.12) can increase with the ion collision frequency.
Because the linearly unstable spectra in figure 1 for the nominal and reduced parameter sets are nearly the same, we use the reduced parameters in table 2 for the simulations.
We note that when the dust temperature is large, it appears that only the Hall-current instability may persist. Figure 2 shows the solution of (2.1) for
$U_{\bot i}/v_{i}=1$
with the reduced parameters in table 2, but with a dust temperature
$T_{d}=20T_{i}$
.
3 Simulations
3.1 Approach
The simulations results described below were performed with a one-dimensional electrostatic particle-in-cell (PIC) code with periodic boundary conditions including a constant electric field
$\boldsymbol{E}$
in the
$\boldsymbol{y}$
direction and a constant magnetic field
$\boldsymbol{B}$
in the
$\boldsymbol{z}$
direction. The plasma species in the PIC simulation consists of singly charged ions that execute an
$\boldsymbol{E}\times \boldsymbol{B}$
drift,
$\boldsymbol{U}_{\bot i}$
in the
$\boldsymbol{x}$
direction and multiply charged, heavy dust grains that are stationary in the simulation reference frame at time
$=$
0. The electrons are modelled as an immobile charge neutralizing fluid, consistent with the arguments used to ignore
$\unicode[STIX]{x1D712}_{e}$
in the discussion on linear theory.
The ions and dust are treated as particles, and both are assumed to collide with the neutral background with a collision frequency
$\unicode[STIX]{x1D708}_{i}$
for the ions and
$\unicode[STIX]{x1D708}_{d}$
for the dust. Both species are modelled as drifting Maxwellians, and a Langevin scattering operator with a constant collision frequency is used to model the collisional effects (Gillespie Reference Gillespie1993). Given the desired ion drift
$U_{\bot i}$
, the
$z$
-directed magnetic field
$B$
, and the collision frequency
$\unicode[STIX]{x1D708}_{i}$
, the required
$y$
-directed electric field
$E$
calculated to be
$$\begin{eqnarray}E=\left[1+\frac{\unicode[STIX]{x1D708}_{i}^{2}}{\unicode[STIX]{x1D714}_{ci}^{2}}\right]\frac{U_{\bot i}B}{c}.\end{eqnarray}$$
Since
$\unicode[STIX]{x1D708}_{i}^{2}/\unicode[STIX]{x1D714}_{ci}^{2}\ll 1$
will be assumed throughout, the ions execute an approximate
$\boldsymbol{E}\times \boldsymbol{B}$
drift.
Once the ion and dust charge densities are calculated at each time step, the Poisson equation can be solved using a standard spectral method (Birdsall & Langdon Reference Birdsall and Langdon1985) to obtain the self-consistent wave potential
$\unicode[STIX]{x1D719}$
.
Quantities in the simulation are normalized to ion quantities at the beginning of the simulation, but with the temperature given by the neutral temperature
$T_{n}$
which is assumed constant. It is assumed that the initial ion temperature at
$t=0$
is
$T_{i0}=T_{n}$
. Thus, temperatures and drift speeds are normalized to
$T_{i0}$
and the associated initial ion thermal speed
$v_{i0}=(T_{i0}/m_{i})^{1/2}$
. Length scales are normalized to the ion Debye length
$\unicode[STIX]{x1D706}_{Di0}$
evaluated at
$T_{i0}$
and the initial ion density
$n_{i0}$
. For the parameters we are using, with
$\unicode[STIX]{x1D714}_{pi}/\unicode[STIX]{x1D714}_{ci}=4$
, the ion gyroradius is related to the ion Debye length via
$\unicode[STIX]{x1D70C}_{i}=4\unicode[STIX]{x1D706}_{Di}$
. In addition,
$\unicode[STIX]{x1D70C}_{i0}$
is the ion gyroradius evaluated at
$T_{i0}$
. The time scales are normalized to the ion plasma frequency
$\unicode[STIX]{x1D714}_{pi}$
evaluated with
$n_{i0}$
. The wave electrostatic potential energy
$e\unicode[STIX]{x1D719}$
is normalized to
$T_{i0}$
(in energy units), and the wave electric field
$\tilde{E}$
is normalized to
$E_{r}=T_{i0}/e\unicode[STIX]{x1D706}_{Di0}$
. The magnetic field is normalized to
$B_{r}=\unicode[STIX]{x1D714}_{pi}m_{i}c/e$
. Put differently, the normalized magnetic field is
$\unicode[STIX]{x1D714}_{ci}/\unicode[STIX]{x1D714}_{pi}$
. For both runs, the system length is
$512\unicode[STIX]{x1D706}_{i0}$
and is divided into
$512$
computational cells. To reduce the numerical noise, the ions and dust are modelled assuming approximately 8 million macro-particles for each species. Finally, it is worth noting that the assumption of
$\unicode[STIX]{x1D714}_{pd}/\unicode[STIX]{x1D714}_{pi}=0.005$
in the reduced parameter set (table 2) allows for a reduction in run time by a factor of 5 compared to the nominal value of
$0.001$
.
3.2 Results
Collisional case
Figure 3 shows the wave energy density versus time for a simulation run with initial conditions corresponding to the parameters in table 2. As can be seen, there appears to be at least two phases in the nonlinear development: there is a faster linear growth phase from
$t\unicode[STIX]{x1D714}_{pi}\sim 3000$
–7000 which saturates at moderate wave energy density, and then a slower linear growth phase from
$t\unicode[STIX]{x1D714}_{pi}\sim (1.7-2.3)\times 10^{4}$
which saturates at a wave energy density which is nearly an order of magnitude larger than that achieved in the first phase. Figure 4 shows the ion and dust temperatures,
$T_{i}$
and
$T_{d}$
, respectively, as a function of time. These temperatures are computed by first calculating the
$x$
-directed kinetic energy density and bulk momentum density for each species as a function of position. From there the pressure in each cell can be obtained, and then the temperature. The results shown in figure 4 are the averages at a given time over all cells. While not shown, there is little change in the ion average velocity in the
$x$
-direction.
Figure 3. Average wave electric field energy density versus time for the collisional case simulation.
Figure 4. Temperature versus time for collisional case simulation: (a) ion temperature, (b) dust temperature.
As can be seen,
$T_{i}$
remains fairly constant, while
$T_{d}$
increases by a factor of approximately 4–5 at saturation of the first phase of the nonlinear development. Then
$T_{d}$
decreases slightly, remaining approximately 3–4 times larger than the initial dust temperature, until about
$t\unicode[STIX]{x1D714}_{pi}\sim 2\times 10^{4}$
where it then increases up to about 50 times the initial dust temperature at saturation of the second phase in the nonlinear development. It should be noted that as
$T_{d}$
increases while
$T_{i}$
remains constant, the dust-acoustic speed
$c_{sd}\sim \unicode[STIX]{x1D714}_{pd}\unicode[STIX]{x1D706}_{Di}$
can become comparable or even smaller than the dust thermal speed, which implies that the usual dust acoustic waves with unmagnetized ions can be heavily damped.
Figures 3 and 4 suggest that, in the first phase, the dust beam cyclotron instability is excited, with a faster growth rate. Then, owing to an increase in dust temperature, the Hall-current instability becomes more dominant and is excited with a slower growth rate, saturating as
$T_{d}$
gets sufficiently large. The power in the different modes at different times seem to corroborate this general picture. Figures 5(a) and 5(b) show the wave power as a function of
$k\unicode[STIX]{x1D70C}_{i}$
at two different times. The power
$|E_{k}|^{2}$
is normalized such that the sum over all
$k$
modes is equal to
$|\tilde{E}^{2}/E_{r}^{2}|\times 512$
. Figure 5(a) shows that the dominant modes at a time during the first growth phase (at
$t\unicode[STIX]{x1D714}_{pi}=5500$
) seem to be relatively discrete, short wavelength modes, with peaks very roughly in the ranges
$k\unicode[STIX]{x1D70C}_{i}\sim 1.5{-}1.8$
,
$k\unicode[STIX]{x1D70C}_{i}\sim 2{-}2.5$
and
$k\unicode[STIX]{x1D70C}_{i}\sim 2.7{-}3.2$
. These wavenumber ranges are reasonably consistent with the three dominant peaks in linear growth rate shown in figure 1. The growth rates estimated from the simulations for these wavenumber regimes, in the time interval
$t\unicode[STIX]{x1D714}_{pi}=5000{-}6500$
, are approximately
$1/2$
the peak growth rates shown in figure 1, basically an average growth rate over those wavelength intervals. Figure 5(b) shows that the dominant modes in the second growth phase, at
$t\unicode[STIX]{x1D714}_{pi}=2\times 10^{4}$
, have much longer wavelength, with roughly
$k\unicode[STIX]{x1D70C}_{i}\sim 0.1{-}0.2$
, which corresponds to that for the Hall-current instability in figure 2. The growth rate estimated from the simulation for this wavenumber regime, in the time interval
$t\unicode[STIX]{x1D714}_{pi}=18\,000{-}21\,000$
, is comparable to the maximum growth rate shown in figure 2.
Figure 5. Power in waves as a function of
$k\unicode[STIX]{x1D70C}_{i0}$
, for collisional case, at time (a)
$t\unicode[STIX]{x1D714}_{pi}=5500$
(b)
$t\unicode[STIX]{x1D714}_{pi}=2\times 10^{4}$
.
Figure 6. Phase space plots and spatial structure of the wave potential for two different times in the collisional case simulation:
$t\unicode[STIX]{x1D714}_{pi}=7000$
(a–c), and
$t\unicode[STIX]{x1D714}_{pi}=22\,000$
(d–f). The ion phase space plots are shown in (a,d), the dust phase space plots in the middle row and the wave potential in (c,f). Note that
$\unicode[STIX]{x1D70C}_{i}=4\unicode[STIX]{x1D706}_{Di}$
for the parameters used.
The above scenario suggests that as
$T_{d}$
increases due to wave trapping, the shorter wavelength modes would be damped by dust Landau damping. The condition for dust to be trapped is (Lampe et al.
Reference Lampe, Manheimer, McBride, Orens, Shanny and Sudan1971)
$$\begin{eqnarray}2Z_{d}e\unicode[STIX]{x1D719}_{tr}=\frac{m_{d}}{2}\left(U_{d}-\frac{\unicode[STIX]{x1D714}_{tr}}{k_{tr}}\right)^{2},\end{eqnarray}$$
where
$k_{tr}$
is the wavenumber of the mode that does the trapping. For
$U_{d}=0$
, and taking
$\unicode[STIX]{x1D714}\sim k\unicode[STIX]{x1D706}_{Di}\unicode[STIX]{x1D714}_{pd}$
, this condition can be written as
$$\begin{eqnarray}\frac{e\unicode[STIX]{x1D719}_{tr}}{T_{i0}}\sim \frac{1}{4}\frac{Z_{d}n_{d}}{n_{i}}.\end{eqnarray}$$
For the parameters we are using, this implies that dust trapping could occur for
$e\unicode[STIX]{x1D719}/T_{i0}\sim 0.1$
. However, dust–neutral collisions may lead to some de-trapping. The effect of dust collisions would be expected to be significant if
$\unicode[STIX]{x1D708}_{d}$
is comparable to the bounce frequency,
$\unicode[STIX]{x1D708}_{bd}$
, of a dust particle in the wave. Taking
$\unicode[STIX]{x1D708}_{bd}=(Z_{d}ek^{2}\unicode[STIX]{x1D719}/m_{d})^{1/2}$
(Nishikawa & Wakatani Reference Nishikawa and Wakatani1990) we have that
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D708}_{bd}}{\unicode[STIX]{x1D714}_{pd}}\sim \left(\frac{n_{i}}{Z_{d}n_{d}}\right)^{1/2}k\unicode[STIX]{x1D706}_{Di}\left(\frac{e\unicode[STIX]{x1D719}}{T_{i0}}\right)^{1/2}.\end{eqnarray}$$
Thus, for the reduced parameter set we are using, we have that
$\unicode[STIX]{x1D708}_{bd}/\unicode[STIX]{x1D708}_{d}\sim 35k\unicode[STIX]{x1D706}_{Di}$
$(e\unicode[STIX]{x1D719}/T_{i0})^{1/2}$
. Figures 6(a–c) and 6(e–f) show the spatial structure of the wave potential
$\unicode[STIX]{x1D719}$
and the ion and dust phase space plots at two different times, respectively:
$t\unicode[STIX]{x1D714}_{pi}=7000$
which is near saturation of the first growth phase, and
$t\unicode[STIX]{x1D714}_{pi}=22\,000$
which is near saturation of the second growth phase. Taking the dominant mode to be in the range of
$k\unicode[STIX]{x1D706}_{Di}\sim 0.5$
(i.e.
$k\unicode[STIX]{x1D70C}_{i}\sim 2$
) at time
$t\unicode[STIX]{x1D714}_{pi}=7000$
, we estimate that
$\unicode[STIX]{x1D708}_{bd}/\unicode[STIX]{x1D708}_{d}\sim 4{-}5$
so dust collisions may play a role in de-trapping of the dust. However, as the wave energy decreases during the time interval from approximately
$t\unicode[STIX]{x1D714}_{pi}\sim (1{-}1.5)\times 10^{4}$
(see figure 3), dust collisions may play a greater role in de-trapping which may explain why
$T_{d}$
remains relatively constant during this time. At
$t\unicode[STIX]{x1D714}_{pi}=22\,000$
, the dominant mode is in the range
$k\unicode[STIX]{x1D706}_{Di}\sim 0.04$
(i.e.
$k\unicode[STIX]{x1D70C}_{i}\sim 0.16$
), while
$|e\unicode[STIX]{x1D719}/T_{i0}|\sim 5$
, so
$\unicode[STIX]{x1D708}_{bd}/\unicode[STIX]{x1D708}_{d}\sim 2{-}3$
and dust collisions may again play a role in de-trapping. As the wave energy continues to increase,
$T_{d}$
increases substantially, to approximately 10–20 times the initial dust temperature, where only the long wavelength Hall-current instability appears to persist. While the concept of ‘temperature’ is very rough for a particle distribution that is not a smooth Maxwellian, as indicated in dust phase space plot in figure 6(e), this interpretation appears reasonably consistent with linear theory based on solving (2.1) with the reduced parameters in table 2, but with a dust temperature
$T_{d}=20T_{i}$
, as shown in figure 2.
The ion temperature appears to remain relatively constant throughout the simulation run, which suggests that ion collisions may play a role in de-trapping. For the dust beam-cyclotron instability, in which the unstable wavelengths are of the order of the ion gyroradius, it may be the case that ions can only remain in resonance with the wave for a time scale of the order of
$\unicode[STIX]{x1D714}_{ci}^{-1}$
, owing to the presence of the magnetic field (see (Forslund, Morse & Nielsen Reference Forslund, Morse and Nielson1971) for the beam-cyclotron instability in an electron–ion plasma). Thus, the linear growth of waves could be modified when
$\unicode[STIX]{x1D714}_{ci}^{-1}$
is greater than the trapping time of an ion in the wave, which is given by the inverse of the ion bounce frequency,
$\unicode[STIX]{x1D708}_{bi}^{-1}\sim (e\unicode[STIX]{x1D719}k^{2}/m_{i})^{-1/2}$
(Forslund et al.
Reference Forslund, Morse and Nielson1971). This implies that roughly
$e\unicode[STIX]{x1D719}/T_{i0}>(k\unicode[STIX]{x1D70C}_{i})^{-2}$
is required. Estimating this condition at
$t\unicode[STIX]{x1D714}_{pi}=7000$
from figure 6(c), taking the dominant wavenumber to be
$k\unicode[STIX]{x1D706}_{Di}\sim 0.5$
(i.e.
$k\unicode[STIX]{x1D70C}_{i}\sim 2$
), we find that it may be marginally satisfied at locations where
$|\unicode[STIX]{x1D719}|$
is maximal. However, ion collisions can lead to de-trapping. The ratio of the ion bounce frequency in the wave,
$\unicode[STIX]{x1D708}_{bi}$
, to the ion collision frequency
$\unicode[STIX]{x1D708}_{i}$
, is roughly
$\unicode[STIX]{x1D708}_{bi}/\unicode[STIX]{x1D708}_{i}\sim 20k\unicode[STIX]{x1D706}_{Di}(e\unicode[STIX]{x1D719}/T_{i0})^{1/2}$
. Taking
$k\unicode[STIX]{x1D706}_{Di}\sim 0.5$
and
$|e\unicode[STIX]{x1D719}/T_{i0}|\sim 0.1$
we find that
$\unicode[STIX]{x1D708}_{bi}/\unicode[STIX]{x1D708}_{i}\sim 2{-}3$
so that collisions can play a role in de-trapping. During the second growth phase, the wavelength of the dominant waves are much larger than the ion gyroradius, so the ions may become trapped in the wave. However, estimating
$\unicode[STIX]{x1D708}_{bi}/\unicode[STIX]{x1D708}_{i}$
at
$t\unicode[STIX]{x1D714}_{pi}=22000$
from figure 6(f), taking
$k\unicode[STIX]{x1D706}_{Di}\sim 0.04$
and
$|e\unicode[STIX]{x1D719}/T_{i0}|\sim 5$
, we find that
$\unicode[STIX]{x1D708}_{bi}/\unicode[STIX]{x1D708}_{i}\sim 2$
so that ion collisions play a role in de-trapping.
Collisionless case
We briefly compare the nonlinear development of the dust beam cyclotron instability in a collisional plasma with that in a collisionless plasma. This is mainly in order to show differences in the wave spectra, and to make connection with prior work on the development of the beam-cyclotron instability in a plasma with magnetized electrons and unmagnetized ions (e.g. Lampe et al. Reference Lampe, Manheimer, McBride, Orens, Shanny and Sudan1971, Reference Lampe, Manheimer, McBride, Orens, Papadopoulos, Shanny and Sudan1972). The latter papers reported that there are two growth phases: a faster growth phase corresponding to the beam-cyclotron instability, and a slower growth phase corresponding to an ion-acoustic instability. It was reported in Lampe et al. (Reference Lampe, Manheimer, McBride, Orens, Shanny and Sudan1971) that when the energy density in the waves excited in the first phase is sufficiently large, the resonance peaks in the beam-cyclotron growth curve are smeared out and the instability goes over to a nonmagnetized ion-acoustic instability. In our case, the ions take the place of electrons, and the dust takes the place of the ions; we expect that the trends in the nonlinear development of the dust beam cyclotron instability may be similar to that in Lampe et al. (Reference Lampe, Manheimer, McBride, Orens, Shanny and Sudan1971).
Figure 7. Average wave electric field energy density versus time for the collisionless case simulation.
Figure 8. Temperature versus time for collisionless case simulation: (a) ion temperature, (b) dust temperature.
Figure 9. Power in waves as a function of
$k\unicode[STIX]{x1D70C}_{i0}$
, for collisionless case, at time (a)
$t\unicode[STIX]{x1D714}_{pi}=800$
(b)
$t\unicode[STIX]{x1D714}_{pi}=4000$
.
Figure 7 shows the wave energy density versus time for a simulation run with initial conditions corresponding to the parameters in table 2, but with
$\unicode[STIX]{x1D708}_{i}=\unicode[STIX]{x1D708}_{d}=0$
. There appear to be two phases in the nonlinear development: a fast growth phase from about
$t\unicode[STIX]{x1D714}_{pi}\sim 600{-}1000$
and then a slower growth phase from
$t\unicode[STIX]{x1D714}_{pi}\sim (1{-}6)\times 10^{3}$
. This second growth phase saturates at a wave energy density which is approximately 30 times larger than that achieved in the first phase. The first growth phase is much faster than in the collisional case, as would be expected. Figure 8 shows the ion and dust temperatures,
$T_{i}$
and
$T_{d}$
, respectively, as a function of time. In this collisionless case, both
$T_{i}$
and
$T_{d}$
increase substantially, as contrasted with the collisional case where
$T_{i}$
remains fairly constant. These trends are similar to those reported in Lampe et al. (Reference Lampe, Manheimer, McBride, Orens, Shanny and Sudan1971, Reference Lampe, Manheimer, McBride, Orens, Papadopoulos, Shanny and Sudan1972) for the analogous beam-cyclotron instability in an electron–ion plasma.
Figure 9 shows the power in different modes at two different times:
$t\unicode[STIX]{x1D714}_{pi}=800$
during the first growth phase, and
$t\unicode[STIX]{x1D714}_{pi}=4000$
during the second growth phase. As can be seen from figure 9(a), in the first growth phase, modes are excited at wavenumbers satisfying the resonance condition
$kU_{\bot ,i}\sim m\unicode[STIX]{x1D714}_{ci}$
. As compared with the collisional case, the wavenumbers are discrete, compared with the broadening of the peaks due to ion collisions in the collisional case. This is consistent with the solution of (2.1) for the reduced parameters in table 2 but with
$\unicode[STIX]{x1D708}_{d}=\unicode[STIX]{x1D708}_{i}=0$
(figure not shown). During the second growth phase, the dominant modes shift to longer wavelengths, as can be seen in figure 9(b). If the second growth phase corresponds to the excitation of a nonmagnetized dust-acoustic instability (in analogy with the beam-cyclotron instability in an electron–ion plasma (Lampe et al.
Reference Lampe, Manheimer, McBride, Orens, Shanny and Sudan1971, Reference Lampe, Manheimer, McBride, Orens, Papadopoulos, Shanny and Sudan1972)), one would expect this shift to longer wavelengths as
$T_{d}$
increases, since dust Landau damping would be weaker at smaller
$k$
.
4 Summary and discussion
We have presented one-dimensional PIC simulations of the nonlinear development of a dust beam-cyclotron instability in a collisional plasma. The instability is driven the ion cross-field
$E\times B$
drift
$U_{\bot }\sim v_{i}$
. In the parameter regime we are considering, the electron dynamics does not contribute to the instability, but just provides charge neutrality. It was found that there are at least two phases in the nonlinear development: a fast growth phase of waves with wavelengths comparable to the ion gyroradius, and a slower growth phase of modes with much longer wavelengths. The behaviour suggests that in the first phase, the dust beam-cyclotron instability generates quasi-discrete short wavelength waves around
$k_{\bot }\unicode[STIX]{x1D70C}_{i}\sim m$
, where the integer
$m$
denotes a harmonic of the ion gyrofrequency. These waves grow to a moderate level of wave energy density and then trap the dust, leading to a moderate increase in the dust temperature. In the second phase, the presence of dominant long wavelength modes suggests that a Hall-current-type instability grows. These waves saturates at an energy density much larger than in the first phase, with a concomitant increase in dust temperature which suggests the saturation may be due to dust Landau damping.
We have also briefly compared the simulation results in the collisional case with a simulation run without collisions mainly in order to show differences in the wave spectra. The simulation showed trends that appear similar to those reported for the analogous beam cyclotron instability in a collisionless electron–ion plasma in Lampe et al. (Reference Lampe, Manheimer, McBride, Orens, Shanny and Sudan1971, Reference Lampe, Manheimer, McBride, Orens, Papadopoulos, Shanny and Sudan1972). In the collisionless case, there are two growth phases, a fast phase and a slower phase. In the fast phase, the dominant modes are discrete short wavelength modes that satisfy the resonance condition
$k_{\bot }\unicode[STIX]{x1D70C}_{i}\sim m$
. In the slower phase, the dominant modes appear to shift to longer wavelength, but yet much shorter wavelength than in the collisional case. Future work should investigate in more detail the behaviour of the instability as the dusty plasma parameters vary from low to high collisionality, i.e. from large to smaller (but still
${>}1$
) ion Hall parameters.
A limitation of the present work is that it is a one-dimensional simulation. While previous linear theory (Rosenberg Reference Rosenberg2014) has shown that growth of the low frequency beam-cyclotron instability in a dusty plasma appears to maximize for purely perpendicular propagation, there is also finite growth at oblique angles. Future work should investigate the effect of this angular dependence on wave saturation levels. Moreover, and probably more important for experiments in high magnetic field devices such as MDPX, there can be electric fields along the magnetic field which lead to ion drifts along
$\boldsymbol{B}$
, in addition to ion cross-field drifts. In order to help interpret possible wave experiments in MDPX for example, future work should comprise two-dimensional simulations taking into account ion drifts both along and across the magnetic field.
Acknowledgement
This work was supported in part by NSF.
