Progress in understanding multi-scale collisionless plasma phenomena requires employing tools which balance computational efficiency and physics fidelity. Collisionless fluid models are able to resolve spatio-temporal scales that are unfeasible with fully kinetic models. However, constructing such models requires truncating the infinite hierarchy of moment equations and supplying an appropriate closure to approximate the unresolved physics. Data-driven methods have recently begun to see increased application to this end, enabling a systematic approach to constructing closures. Here, we use sparse regression to search for heat flux closures for one-dimensional electrostatic plasma phenomena. We examine OSIRIS particle-in-cell simulation data of Landau-damped Langmuir waves and two-stream instabilities. Sparse regression consistently identifies six terms as physically relevant, together regularly accounting for more than 95 % of the variation in the heat flux. We further quantify the relative importance of these terms under various circumstances and examine their dependence on parameters such as thermal speed and growth/damping rate. The results are discussed in the context of previously known collisionless closures and linear collisionless theory.

We investigate the one-dimensional non-relativistic Weibel instability through the capture of anisotropic pressure tensor dynamics using an implicit 10-moment fluid model that employs the electromagnetic Darwin approximation. The results obtained from the 10-moment model are compared with an implicit particle-in-cell simulation. The linear growth rates obtained from the numerical simulations are in good agreement with the theoretical fluid and kinetic dispersion relations. The fluid dispersion relations are derived using Maxwell’s equations and the Darwin approximation. We also show that the magnetohydrodynamic approximation can be used to model the Weibel instability if one accounts for an anisotropic pressure tensor and unsteady terms in the generalised Ohm’s law. In addition, we develop a preliminary theory for the saturation magnetic field strength of the Weibel instability, showing good agreement with the numerical results.

We derive a set of simplified equations that can be used for numerical studies of reduced magnetohydrodynamic turbulence within a small patch of the radially expanding solar wind. We allow the box to be either stationary in the Sun’s frame or to be moving at an arbitrary velocity along the background magnetic-field lines, which we take to be approximately radial. We focus in particular on the case in which the box moves at the same speed as outward-propagating Alfvén waves. To aid in the design and optimization of future numerical simulations, we express the equations in terms of scalar potentials and Clebsch coordinates. The equations we derive will be particularly useful for conducting high-resolution numerical simulations of reflection-driven magnetohydrodynamic turbulence in the solar wind, and may also be useful for studying turbulence within other astrophysical outflows.

An analysis of the divertor designs for the Infinity Two fusion pilot plant (FPP) baseline plasma design is presented. The divertor uses an $m=5$, $n=4$ magnetic island chain, where m is the poloidal number and n is the toroidal number. Two divertor designs are presented. A classical divertor that is similar to the Wendelstein 7-X island divertor is analyzed using diffusive field-line following and the fluid code EMC3-Lite. For a baseline $800\text{ MW}$ operating point in Infinity Two, the conditions where the heat flux on the divertor plate remains in the acceptable region are analyzed. In addition a related, but different and novel large island backside divertor (LIBD) design is shown. The LIBD promises improved neutral pumping by closing the divertor through the use of baffling and with a structure inside the island, thus preventing neutralized plasma particles from reente ring the plasma.

Intermittency as it occurs in fast dynamos in the magnetohydrodynamics (MHD) framework is evaluated through the examination of relations between normalized moments at third order (skewness 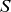$S$) and fourth order (kurtosis 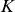$K$) for both the velocity and magnetic field, and for their local dissipations. As investigated by several authors in various physical contexts such as fusion plasmas (Krommes 2008 Phys. Plasmas 15, 030703), climate evolution (Sura & Sardeshmukh 2008 J. Phys. Oceano. 38, 639-647), fluid turbulence or rotating stratified flows (Pouquet et al. 2023 Atmosphere 14, 01375), approximate parabolic 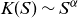$K(S)\sim S^\alpha$ laws emerge whose origin may be related to the applicability of intermittency models to their dynamics. The results analyzed herein are obtained through direct numerical simulations of MHD flows for both Taylor–Green and Arnold–Beltrami–Childress forcing at moderate Reynolds numbers, and for up to 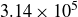$3.14 \times 10^5$ turn-over times. We observe for the dissipation 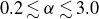$0.2 \lesssim \alpha \lesssim 3.0$, an evaluation that varies with the field, the forcing and when filtering for high-skewness intermittent structures. When using the She & Lévêque (1994) Phys. Rev. Lett. 72, 336-339 intermittency model, one can compute 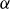$\alpha$ analytically; we then find 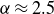$\alpha \approx 2.5$, clearly differing from a (strict) parabolic scaling, a result consistent with the numerical data.