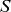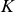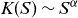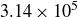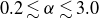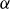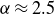1. Introduction
One striking property of turbulent flows is their lack of predictability, as well as their intermittency, associated with the presence of intense and isolated patterns at small scales, such as vortex filaments and current sheets, or coherent structures at large scale. Such extreme events can be assessed through their probability distribution functions (PDFs), and thus through their normalized moments such as the skewness and kurtosis (definitions are given in § 2). These intense structures have been identified in many experiments, observations and direct numerical simulations (see for recent reviews e.g. Matthaeus et al. Reference Matthaeus, Wan, Servidio, Greco, Osman, Oughton and Dmitruk2015; Yeung, Zhai & Sreenivasan Reference Yeung, Zhai and Sreenivasan2015; Chen Reference Chen2016; Camporeale et al. Reference Camporeale, Sorriso-Valvo, Califano and Retinó2018; Ergun Reference Ergun2020; Schekochihin Reference Schekochihin2022). The ensuing dissipation is found in a reduced volume of the system, in both neutral fluids (Bradshaw, Farhat & Grujic Reference Bradshaw, Farhat and Grujic2019; Rafner et al. Reference Rafner, Grujic, Bach, Bærentzen, Gervang, Jia R.and Leinweber and Misztal, M.and Sherson2021; Buaria, Pumir & Bodenschatz Reference Buaria, Pumir and Bodenschatz2022) and magnetohydrodynamics (MHD) (see e.g. Politano, Pouquet & Sulem Reference Politano, Pouquet and Sulem1995; Meneguzzi et al. Reference Meneguzzi, Politano, Pouquet and Zolver1996; Mallet, Schekochihin & Chandran Reference Mallet, Schekochihin and Chandran2017; Zhdankin, Boldyrev & Mason Reference Zhdankin, Boldyrev and Mason2017; Adhikari et al. Reference Adhikari, Shay, Parashar, Pyakurel, Matthaeus, Godzieba, Stawarz, Eastwood and Dahlin2020). This physical intermittency volume can be in fact smaller than for fully developed turbulence, as shown explicitly in the presence of gravity waves (Marino et al. Reference Marino, Feraco, Primavera, Pumir, Pouquet and Rosenberg2022). It is also found in the ocean (van Haren et al. Reference van Haren, Cimatoribus, Cyr and Gostiaux2016), as well as in clear air turbulence, the origin of which remains rather ill understood although Kelvin–Helmholtz and shear instabilities are likely to be the culprit (Imazio et al. Reference Imazio, Mininni, Godoy, Rivaben and Dörnbrack2023), as for the other examples given here. Similar observations are documented for plasma disruptions.
Intermittency can be characterized in many ways, such as when evaluating anomalous exponents of structure functions. Perhaps more directly, one can assess when and where normalized third- and fourth-order moments, skewness
![]() $S$
and kurtosis
$S$
and kurtosis
![]() $K$
, differ from their Gaussian values. There is a long history of such measurements; for example, both skewness and kurtosis have been used to map a flow, such as in meandering jets in the ocean (Hughes, Thompson & Wilson Reference Hughes, Thompson and Wilson2010), or in climate data reanalysis (Petoukhov et al. Reference Petoukhov, Eliseev, Klein and Oesterle2008).
$K$
, differ from their Gaussian values. There is a long history of such measurements; for example, both skewness and kurtosis have been used to map a flow, such as in meandering jets in the ocean (Hughes, Thompson & Wilson Reference Hughes, Thompson and Wilson2010), or in climate data reanalysis (Petoukhov et al. Reference Petoukhov, Eliseev, Klein and Oesterle2008).
One way to condense the data further is to look for
![]() $K(S)$
relations, often found to be close to parabolic in a variety of contexts (see Pouquet et al. Reference Pouquet, Rosenberg, Marino and Mininni2023 and references therein for a recent review), e.g. for the Navier–Stokes (NS) equations, in the presence or not of stratification and/or rotation, as relevant to the atmosphere, the ocean and climate (Lenschow, Mann & Kristensen Reference Lenschow, Mann and Kristensen1994; Sura & Sardeshmukh Reference Sura and Sardeshmukh2008). Such quasi-parabolic laws were also found in laboratory and astrophysical plasmas (see for example Labit et al. Reference Labit, Furno, Fasoli, Diallo, Müller, Plyushchev, Podestà and Poli2007; Krommes Reference Krommes2008; Sattin et al. Reference Sattin2009; Garcia Reference Garcia2012; Guszejnov et al. Reference Guszejnov, Lazanyi, Bencze and Zoletnik2013; Mezaoui, Hamza & Jayachandran Reference Mezaoui, Hamza and Jayachandran2014; Furno et al. Reference Furno2015; Miranda et al. Reference Miranda, Schelin, Chian and Ferreira2018). More recently, Sladkomedova et al. (Reference Sladkomedova, Cziegler, Field, Schekochihin and Ivanov2023) analyzed the intermittency of the density in MAST (Mega Ampere Spherical Tokamak) plasmas, and found that the data agrees with the
$K(S)$
relations, often found to be close to parabolic in a variety of contexts (see Pouquet et al. Reference Pouquet, Rosenberg, Marino and Mininni2023 and references therein for a recent review), e.g. for the Navier–Stokes (NS) equations, in the presence or not of stratification and/or rotation, as relevant to the atmosphere, the ocean and climate (Lenschow, Mann & Kristensen Reference Lenschow, Mann and Kristensen1994; Sura & Sardeshmukh Reference Sura and Sardeshmukh2008). Such quasi-parabolic laws were also found in laboratory and astrophysical plasmas (see for example Labit et al. Reference Labit, Furno, Fasoli, Diallo, Müller, Plyushchev, Podestà and Poli2007; Krommes Reference Krommes2008; Sattin et al. Reference Sattin2009; Garcia Reference Garcia2012; Guszejnov et al. Reference Guszejnov, Lazanyi, Bencze and Zoletnik2013; Mezaoui, Hamza & Jayachandran Reference Mezaoui, Hamza and Jayachandran2014; Furno et al. Reference Furno2015; Miranda et al. Reference Miranda, Schelin, Chian and Ferreira2018). More recently, Sladkomedova et al. (Reference Sladkomedova, Cziegler, Field, Schekochihin and Ivanov2023) analyzed the intermittency of the density in MAST (Mega Ampere Spherical Tokamak) plasmas, and found that the data agrees with the
![]() $K(S)$
model given by Garcia (Reference Garcia2012) (see also Guszejnov et al. Reference Guszejnov, Lazanyi, Bencze and Zoletnik2013; Losada, Theodorsen & Garcia Reference Losada, Theodorsen and Garcia2023).Footnote
1
$K(S)$
model given by Garcia (Reference Garcia2012) (see also Guszejnov et al. Reference Guszejnov, Lazanyi, Bencze and Zoletnik2013; Losada, Theodorsen & Garcia Reference Losada, Theodorsen and Garcia2023).Footnote
1
Detailed knowledge of intermittency in plasmas and turbulent systems in general may lead to a better understanding of their PDFs and of the dissipation mechanisms at play. It is in this context that we want to examine in this paper the intermittent properties of MHD through the possible relationship between excess kurtosis and skewness for the velocity and magnetic field, as well as for their local dissipation. MHD has, of course, many different regimes, and we concentrate here on one subset, namely that of the fast dynamo in its nonlinear phase and at moderate Reynolds number for which long runs are available, up to in excess of
![]() $10^5 \tau _{nl}$
, where
$10^5 \tau _{nl}$
, where
is the turn-over time of the turbulence based on the large-scale velocity
![]() $V_{rms}$
and on the integral length scale
$V_{rms}$
and on the integral length scale
![]() $L_{int}$
. In the next section are written the equations and definitions needed for our analysis of numerical MHD data for a fast dynamo regime, as well as information on the direct numerical simulations (DNSs) employed herein. In § 3, we analyze the numerical results, and in § 4 we give an interpretation of them within a specific model of intermittency. The last section presents a discussion and our conclusions.
$L_{int}$
. In the next section are written the equations and definitions needed for our analysis of numerical MHD data for a fast dynamo regime, as well as information on the direct numerical simulations (DNSs) employed herein. In § 3, we analyze the numerical results, and in § 4 we give an interpretation of them within a specific model of intermittency. The last section presents a discussion and our conclusions.
2. Equations and numerical set-up
2.1. Equations and definitions
The equations for MHD in the incompressible case are written as usual as
together with
![]() $\nabla \cdot \boldsymbol{u}=0, \nabla \cdot \boldsymbol{b}=0$
; here,
$\nabla \cdot \boldsymbol{u}=0, \nabla \cdot \boldsymbol{b}=0$
; here,
![]() $\boldsymbol{u}, \boldsymbol{b}$
are the velocity and magnetic field (in Alfvén velocity units),
$\boldsymbol{u}, \boldsymbol{b}$
are the velocity and magnetic field (in Alfvén velocity units),
![]() $P^\star$
is the total pressure,
$P^\star$
is the total pressure,
![]() $\nu, \eta$
are the viscosity and magnetic diffusivity and
$\nu, \eta$
are the viscosity and magnetic diffusivity and
![]() $\boldsymbol{F}_V$
is a forcing term. We will use in this paper two types of forcing. The first one is the ABC (Arnold–Beltrami–Childress) forcing, which is a superposition of Beltrami vortices and thus fully helical; it is defined as
$\boldsymbol{F}_V$
is a forcing term. We will use in this paper two types of forcing. The first one is the ABC (Arnold–Beltrami–Childress) forcing, which is a superposition of Beltrami vortices and thus fully helical; it is defined as
The ABC flow is an eigenfunction of the curl, and it is an exact solution of the Euler equations; thus, for large enough viscosity, it is stable but turbulence develops as the Reynolds number
![]() $R_V$
increases. We also take the Taylor–Green (TG) forcing written as
$R_V$
increases. We also take the Taylor–Green (TG) forcing written as
with
![]() $f_0^{tg}=3$
. This forcing is globally non-helical, but it can be viewed in fact as an assembly of helical patches of both signs and varied intensities.
$f_0^{tg}=3$
. This forcing is globally non-helical, but it can be viewed in fact as an assembly of helical patches of both signs and varied intensities.
We solved numerically our MHD system in a fully periodic box using a classic pseudo-spectral solver, involving a
![]() $2/3$
dealiasing technique with a parallel CPU-MPI code (CUBBY; Ponty et al. Reference Ponty, Mininni, Montgomery, Pinton, Politano and Pouquet2005). With these two forcings, we compute four simulations altogether, for up to hundreds of thousands of eddy turn-over times, and we record the same number of snapshots for the three-dimensional field components for
$2/3$
dealiasing technique with a parallel CPU-MPI code (CUBBY; Ponty et al. Reference Ponty, Mininni, Montgomery, Pinton, Politano and Pouquet2005). With these two forcings, we compute four simulations altogether, for up to hundreds of thousands of eddy turn-over times, and we record the same number of snapshots for the three-dimensional field components for
![]() $\textbf{v}$
and
$\textbf{v}$
and
![]() $\textbf{b}$
. Some of the data and a few of the statistical properties of these runs are given in table 1.
$\textbf{b}$
. Some of the data and a few of the statistical properties of these runs are given in table 1.
Table 1. Characteristics of the runs, with the linear resolution
![]() $n_p$
of the cubic grid,
$n_p$
of the cubic grid,
![]() $\nu$
the viscosity, the Reynolds number
$\nu$
the viscosity, the Reynolds number
![]() $R_V= L_{int} V_{rms}/\nu$
and Taylor Reynolds number
$R_V= L_{int} V_{rms}/\nu$
and Taylor Reynolds number
![]() $R_\lambda =\lambda V_{rms}/\nu$
;
$R_\lambda =\lambda V_{rms}/\nu$
;
![]() $R_N= \eta _v n_p/3$
is the so-called Kaneda criterion based on the resolution in terms of the Kolmogorov dissipation length
$R_N= \eta _v n_p/3$
is the so-called Kaneda criterion based on the resolution in terms of the Kolmogorov dissipation length
![]() $\eta _v$
. TG denotes Taylor–Green runs, and ABC denotes ABC runs (see text). For each run,
$\eta _v$
. TG denotes Taylor–Green runs, and ABC denotes ABC runs (see text). For each run,
![]() $T_{max}$
is its total duration, with
$T_{max}$
is its total duration, with
![]() $\tau _{nl}$
in these units between 1 and 2. For the magnetic variables, we give the magnetic Reynolds number
$\tau _{nl}$
in these units between 1 and 2. For the magnetic variables, we give the magnetic Reynolds number
![]() $R_M= L_{int} V_{rms}/\eta$
, the magnetic Prandtl number
$R_M= L_{int} V_{rms}/\eta$
, the magnetic Prandtl number
![]() $P_m=\nu /\eta$
and
$P_m=\nu /\eta$
and
![]() $r=R_M/R_M^C$
is the ratio of the magnetic Reynolds number to the (approximate) critical value for the threshold of the dynamo. All these non-dimensional numbers need different definition of scales, like the integral scale
$r=R_M/R_M^C$
is the ratio of the magnetic Reynolds number to the (approximate) critical value for the threshold of the dynamo. All these non-dimensional numbers need different definition of scales, like the integral scale
![]() $L_{int}=2 \pi \sum E(k)/k/\sum E(k)$
defined using the isotropic energy spectrum computed along the simulation at each wavenumber
$L_{int}=2 \pi \sum E(k)/k/\sum E(k)$
defined using the isotropic energy spectrum computed along the simulation at each wavenumber
![]() $k$
, the Taylor scale
$k$
, the Taylor scale
![]() $\lambda =\sqrt {10}\eta _v R_V^{1/4}=\sqrt {10}L_{int}R_V^{-1/2}$
in the inertial range and the Kolmogorov scale
$\lambda =\sqrt {10}\eta _v R_V^{1/4}=\sqrt {10}L_{int}R_V^{-1/2}$
in the inertial range and the Kolmogorov scale
![]() $\eta _v= [\frac {\epsilon _v}{\nu ^3}]^{-1/4} = L_{int}R_V^{-3/4}$
at the onset of the dissipation range. We need also one characteristic velocity which is usually taken as the root mean square of the kinetic energy
$\eta _v= [\frac {\epsilon _v}{\nu ^3}]^{-1/4} = L_{int}R_V^{-3/4}$
at the onset of the dissipation range. We need also one characteristic velocity which is usually taken as the root mean square of the kinetic energy
![]() $V_{rms}= \sqrt {2 \sum E(k)}$
. The nonlinear time is taken as
$V_{rms}= \sqrt {2 \sum E(k)}$
. The nonlinear time is taken as
![]() $\tau _{nl}= L_{int}/V_{rms}$
. All the scales and velocity are averaged in time as the simulations develop.
$\tau _{nl}= L_{int}/V_{rms}$
. All the scales and velocity are averaged in time as the simulations develop.

2.2. Brief description of the runs
The dynamo problem, concerning the generation of magnetic fields at both large and small scales, is a long-standing topic (see Brandenburg & Subramanian Reference Brandenburg and Subramanian2005; Rincon Reference Rincon2019 for thorough recent reviews). In the context of this paper, we analyze four simulation runs, focusing on the turbulent dynamo regime. In these simulations, the (fast) dynamo is triggered when the magnetic Reynolds number
![]() $R_M$
exceeds a threshold that depends on the magnetic Prandtl number
$R_M$
exceeds a threshold that depends on the magnetic Prandtl number
![]() $P_m=\nu /\eta$
(Ponty et al. Reference Ponty, Mininni, Montgomery, Pinton, Politano and Pouquet2005), as seen in run TG3. Sub-critical dynamos can also be observed, where magnetically induced changes to the velocity field play a role, such as in run TG1, which is close to the onset of dynamo action, and living on the sub-critical branch (Ponty et al. Reference Ponty, Laval, Dubrulle, Daviaud and Pinton2007). It is also worth noting that the Lorenz force’s feedback on the velocity field can influence the so-called ‘on–off’ intermittency of the dynamo, as explored in detail by Alexakis & Ponty (Reference Alexakis and Ponty2008) in the context of the ABC runs ABC1 and ABC2. These runs are notable for their short off phases, during which the magnetic field becomes weak enough to revert the system to a hydrodynamic state. The dynamo comes back quickly, with a return to an MHD equilibrium (see figure 1 below). We thus finally have two different types of dynamo turbulence, with a large amount of fluctuations which are analyzed in the next sections, examining the behavior of the third- and fourth-order normalized moment statistics using the full-space temporal field data.
$P_m=\nu /\eta$
(Ponty et al. Reference Ponty, Mininni, Montgomery, Pinton, Politano and Pouquet2005), as seen in run TG3. Sub-critical dynamos can also be observed, where magnetically induced changes to the velocity field play a role, such as in run TG1, which is close to the onset of dynamo action, and living on the sub-critical branch (Ponty et al. Reference Ponty, Laval, Dubrulle, Daviaud and Pinton2007). It is also worth noting that the Lorenz force’s feedback on the velocity field can influence the so-called ‘on–off’ intermittency of the dynamo, as explored in detail by Alexakis & Ponty (Reference Alexakis and Ponty2008) in the context of the ABC runs ABC1 and ABC2. These runs are notable for their short off phases, during which the magnetic field becomes weak enough to revert the system to a hydrodynamic state. The dynamo comes back quickly, with a return to an MHD equilibrium (see figure 1 below). We thus finally have two different types of dynamo turbulence, with a large amount of fluctuations which are analyzed in the next sections, examining the behavior of the third- and fourth-order normalized moment statistics using the full-space temporal field data.
3. Analysis of the results
3.1. Field gradient tensors, skewness and kurtosis
Concerning the data points for measurements, which must be statistically independent, they are taken approximately every
![]() $\tau _{nl}$
; we recall that measurement errors go as
$\tau _{nl}$
; we recall that measurement errors go as
![]() $\sqrt {6/N_s}$
, with
$\sqrt {6/N_s}$
, with
![]() $N_s$
the number of independent data points (see e.g. Sura & Sardeshmukh Reference Sura and Sardeshmukh2008). Large samples are needed also because a parabolic fit is quite sensitive to extreme values. Note that it is shown in (Wan et al. Reference Wan, Oughton, Servidio and Matthaeus2010), in the context of two-dimensional (2-D) MHD turbulence, that an estimate of the kurtosis at small scales requires, in the framework of the DNSs analyzed in that paper, that the (Kolmogorov) dissipation scale be at least twice as large as the cutoff
$N_s$
the number of independent data points (see e.g. Sura & Sardeshmukh Reference Sura and Sardeshmukh2008). Large samples are needed also because a parabolic fit is quite sensitive to extreme values. Note that it is shown in (Wan et al. Reference Wan, Oughton, Servidio and Matthaeus2010), in the context of two-dimensional (2-D) MHD turbulence, that an estimate of the kurtosis at small scales requires, in the framework of the DNSs analyzed in that paper, that the (Kolmogorov) dissipation scale be at least twice as large as the cutoff
![]() $k_{max}=n_p/3$
; this condition is well fulfilled by the runs of table 1 (see parameter
$k_{max}=n_p/3$
; this condition is well fulfilled by the runs of table 1 (see parameter
![]() $R_N$
).
$R_N$
).
We analyze the data using the point-wise rates of dissipation of the kinetic and magnetic energy,
![]() $ \epsilon _v(\boldsymbol{x}), \epsilon _m(\boldsymbol{x})$
. They are expressed in terms of the symmetric part of the velocity gradient tensor, namely the strain tensor
$ \epsilon _v(\boldsymbol{x}), \epsilon _m(\boldsymbol{x})$
. They are expressed in terms of the symmetric part of the velocity gradient tensor, namely the strain tensor
![]() $S^v_{ij}$
$S^v_{ij}$
and of the magnetic current density, viz.
![]() $\epsilon _m(\boldsymbol{x}) = {\eta } \boldsymbol{j}^2(\boldsymbol{x})$
. For completeness, we also define the symmetric part of the magnetic field gradient tensor, namely
$\epsilon _m(\boldsymbol{x}) = {\eta } \boldsymbol{j}^2(\boldsymbol{x})$
. For completeness, we also define the symmetric part of the magnetic field gradient tensor, namely
Note that
![]() $S^m_{ij}$
is a pseudo (axial) tensor. The standard expressions for the integrated (space-averaged) kinetic, magnetic and total energy dissipation rates, can respectively be written also as
$S^m_{ij}$
is a pseudo (axial) tensor. The standard expressions for the integrated (space-averaged) kinetic, magnetic and total energy dissipation rates, can respectively be written also as
with
![]() $\boldsymbol {\omega }=\nabla \times \boldsymbol{u}$
the vorticity. Finally, the skewness and excess kurtosis are written below for a scalar field
$\boldsymbol {\omega }=\nabla \times \boldsymbol{u}$
the vorticity. Finally, the skewness and excess kurtosis are written below for a scalar field
![]() $f$
, with
$f$
, with
![]() $S_f=0, K_f=0$
for a Gaussian distribution, with the kurtosis (or flatness) being defined as
$S_f=0, K_f=0$
for a Gaussian distribution, with the kurtosis (or flatness) being defined as
![]() $F_f =K_f+3$
$F_f =K_f+3$
3.2.
Some models for
 $K(S)$
relations
$K(S)$
relations
A
![]() $K(S)$
parabolic law has been derived explicitly in Sura & Sardeshmukh (Reference Sura and Sardeshmukh2008) for a model of oceanic sea-surface temperature anomalies, based on the dynamics of a specific linear Langevin model with both additive and multiplicative noises. Analyzing the corresponding Fokker–Planck equation for the stationary PDF, these authors can show analytically that, in the limit of weak multiplicative noise, one has
$K(S)$
parabolic law has been derived explicitly in Sura & Sardeshmukh (Reference Sura and Sardeshmukh2008) for a model of oceanic sea-surface temperature anomalies, based on the dynamics of a specific linear Langevin model with both additive and multiplicative noises. Analyzing the corresponding Fokker–Planck equation for the stationary PDF, these authors can show analytically that, in the limit of weak multiplicative noise, one has
![]() $K(S)= 3S^2/2$
. Multiple other studies show the plausibility of a Langevin model for parabolic
$K(S)= 3S^2/2$
. Multiple other studies show the plausibility of a Langevin model for parabolic
![]() $K(S)$
behaviors in different contexts as exemplified e.g. in Hasselmann (Reference Hasselmann1962) and Sattin et al. (Reference Sattin2009) (see also Pouquet et al. (Reference Pouquet, Marino, Politano, Ponty and Rosenberg2025) for nonlinear Langevin models). Note that, in a Langevin equation, in a sense, one is getting rid of the closure problem for turbulent motions since it is linear, with the complex nonlinear small-scale dynamics bundled up in a rapid stochastic forcing with an assumption of (mostly) local interactions among these fast motions.
$K(S)$
behaviors in different contexts as exemplified e.g. in Hasselmann (Reference Hasselmann1962) and Sattin et al. (Reference Sattin2009) (see also Pouquet et al. (Reference Pouquet, Marino, Politano, Ponty and Rosenberg2025) for nonlinear Langevin models). Note that, in a Langevin equation, in a sense, one is getting rid of the closure problem for turbulent motions since it is linear, with the complex nonlinear small-scale dynamics bundled up in a rapid stochastic forcing with an assumption of (mostly) local interactions among these fast motions.
In fact, models in the framework of fusion plasmas have also been written, for example in the context of magnetically confined experiments. In Garcia (Reference Garcia2012), the dynamics, as for dissipation events, is viewed as a random sequence of bursts as opposed to a quasi-continuum. These bursts are occurring independently and following a Poisson process. When taking for the shape of these bursts a sharp rise and a slow exponential decay, one can compute
![]() $K(S)$
relations which, for an exponential distribution of burst amplitudes, becomes
$K(S)$
relations which, for an exponential distribution of burst amplitudes, becomes
![]() $K(S)=3/2(S^2-1)$
.
$K(S)=3/2(S^2-1)$
.

Figure 1. Run ABC2: temporal evolutions, with kinetic variables in blue and magnetic ones in red. Top, left and right: kinetic energy and its dissipation,
![]() $\epsilon _v$
. Middle, left and right: magnetic energy and its dissipation,
$\epsilon _v$
. Middle, left and right: magnetic energy and its dissipation,
![]() $\epsilon _m=\eta (\,\boldsymbol{j}^2)$
. Note the different units on axes, and the lin–log scale for magnetic energy. Bottom: probability density functions of the kinetic and magnetic energies (two left plots), and of their dissipation (two right plots), with lin–log plots used for the latter.
$\epsilon _m=\eta (\,\boldsymbol{j}^2)$
. Note the different units on axes, and the lin–log scale for magnetic energy. Bottom: probability density functions of the kinetic and magnetic energies (two left plots), and of their dissipation (two right plots), with lin–log plots used for the latter.

Figure 2. Similar plots as in figure 1 but now for the TG3 run.
3.3. Collecting the spatio-temporal data for further analysis
Our methodology is the following. For each field variable at a fixed observation time
![]() $T_O$
, as for the vertical component of the velocity
$T_O$
, as for the vertical component of the velocity
![]() $v_z(\boldsymbol{x}, T_O)$
, or the magnetic energy dissipation
$v_z(\boldsymbol{x}, T_O)$
, or the magnetic energy dissipation
![]() $\eta \boldsymbol{j}^2(\boldsymbol{x}, T_O)$
, the data are collected roughly every turn-over time
$\eta \boldsymbol{j}^2(\boldsymbol{x}, T_O)$
, the data are collected roughly every turn-over time
![]() $\tau _{nl}$
, for in excess of
$\tau _{nl}$
, for in excess of
![]() $5 \times 10^4$
outputs, as shown in column
$5 \times 10^4$
outputs, as shown in column
![]() $T_{max}$
in table 1. For each full-cube temporal data output at
$T_{max}$
in table 1. For each full-cube temporal data output at
![]() $T_O$
the spatially dependent 3-D fields we analyze are computed point-wise at each
$T_O$
the spatially dependent 3-D fields we analyze are computed point-wise at each
![]() $\boldsymbol{x}$
location in the
$\boldsymbol{x}$
location in the
![]() $n_p^3$
data cube. The PDFs are constructed for these various fields, at that fixed time
$n_p^3$
data cube. The PDFs are constructed for these various fields, at that fixed time
![]() $T_O$
, and their second, third and fourth moments are evaluated to yield skewness and kurtosis for that time index
$T_O$
, and their second, third and fourth moments are evaluated to yield skewness and kurtosis for that time index
![]() $T_O$
. These data are then assembled in
$T_O$
. These data are then assembled in
![]() $K(S)$
plots for the different physical variables of interest. In figures 3 and 4, the time arrow of the data is indicated by the color of the points in the scatter plots, with a rainbow code as given by the color bar at the left of the plots, with purple at early times and red at late times. We note that, having in excess of
$K(S)$
plots for the different physical variables of interest. In figures 3 and 4, the time arrow of the data is indicated by the color of the points in the scatter plots, with a rainbow code as given by the color bar at the left of the plots, with purple at early times and red at late times. We note that, having in excess of
![]() $5 \times 10^4$
time stamps
$5 \times 10^4$
time stamps
![]() $T_O^{(i)}$
for all runs, the error on the skewness is less than
$T_O^{(i)}$
for all runs, the error on the skewness is less than
![]() $0.025$
, and twice that for the kurtosis. As expected, these systems achieve statistical equilibria rapidly, in a few
$0.025$
, and twice that for the kurtosis. As expected, these systems achieve statistical equilibria rapidly, in a few
![]() $\tau _{nl}$
(see figures 1and 2 giving the whole time span of the runs for the kinetic and magnetic energies).
$\tau _{nl}$
(see figures 1and 2 giving the whole time span of the runs for the kinetic and magnetic energies).
Note that this methodology does not correspond to a spatial analysis of intermittency at a fixed time, such as the first maximum of dissipation, given the moderate spatial resolution of the runs analyzed herein. This would lead to a study of the localization and intensity of extreme events at that time, but this is not the purpose of this study. Rather, we instead consider solely here the statistical variations over long times of the spatial intermittency of several field statistics in a global way. We do that in terms of overall variation of non-dimensionalized moments of various functionals of the velocity and magnetic fields as they evolve in time. With samples taken roughly every turn-over time, the statistical data points can be considered as independent. This leads to an investigation of the scatter in values of both
![]() $K$
and
$K$
and
![]() $S$
for a sample of field functionals, and thus of the
$S$
for a sample of field functionals, and thus of the
![]() $K(S)$
relationships that may emerge for them, with each point on the scatter plots of figures 3 and 4 corresponding to a given
$K(S)$
relationships that may emerge for them, with each point on the scatter plots of figures 3 and 4 corresponding to a given
![]() $T_O$
. We finally note that these analyses require substantial storage capabilities even at moderate spatial resolutions, so that the various statistical variables of interest and their moments are better computed a priori, and stored as the runs progress.
$T_O$
. We finally note that these analyses require substantial storage capabilities even at moderate spatial resolutions, so that the various statistical variables of interest and their moments are better computed a priori, and stored as the runs progress.
3.4. Overall data analysis
We give for the ABC2 flow (figure 1) and for the TG3 case (figure 2) the temporal evolution of the kinetic (top) and magnetic (middle) energy as a function of time on the left, and on the right of their respective total dissipations,
![]() $\epsilon _{V,M}$
. Note that time is expressed in output counts, with a turn-over time being roughly twice that. At the bottom are given the energy PDFs for the velocity (blue, leftmost) and the magnetic field (red, rightmost plots.) In all cases, there are sustained fluctuations in the amplitude of the fields, and in the case of the ABC run, lapses in both kinetic and magnetic energy corresponding to the on–off mechanism. This is directly related to the fact that the PDFs, in that case, have two relative maxima (with one peak close to zero for the magnetic field), whereas in the case of the TG forcing, the structure of the PDFs is closer to being unimodal. We note that exponential fits in the case of the dissipation fields are plausible, but not yet very strongly marked given the moderate range of Reynolds numbers in these runs.
$\epsilon _{V,M}$
. Note that time is expressed in output counts, with a turn-over time being roughly twice that. At the bottom are given the energy PDFs for the velocity (blue, leftmost) and the magnetic field (red, rightmost plots.) In all cases, there are sustained fluctuations in the amplitude of the fields, and in the case of the ABC run, lapses in both kinetic and magnetic energy corresponding to the on–off mechanism. This is directly related to the fact that the PDFs, in that case, have two relative maxima (with one peak close to zero for the magnetic field), whereas in the case of the TG forcing, the structure of the PDFs is closer to being unimodal. We note that exponential fits in the case of the dissipation fields are plausible, but not yet very strongly marked given the moderate range of Reynolds numbers in these runs.
Figure 3 gives
![]() $K(S)$
for various fields; at top, we display the
$K(S)$
for various fields; at top, we display the
![]() $K(S)$
relationship for the z-component of the velocity, the square vorticity and the kinetic energy dissipation, namely
$K(S)$
relationship for the z-component of the velocity, the square vorticity and the kinetic energy dissipation, namely
![]() $K_{v_z}(\boldsymbol{x}), K_{\omega ^2}(\boldsymbol{x})$
and
$K_{v_z}(\boldsymbol{x}), K_{\omega ^2}(\boldsymbol{x})$
and
![]() $K_{\epsilon _v}(\boldsymbol{x})$
. At bottom we plot the equivalent fields for the magnetic induction, namely
$K_{\epsilon _v}(\boldsymbol{x})$
. At bottom we plot the equivalent fields for the magnetic induction, namely
![]() $K_{b_z}(\boldsymbol{x}), K_{\sigma _m}(\boldsymbol{x})$
and
$K_{b_z}(\boldsymbol{x}), K_{\sigma _m}(\boldsymbol{x})$
and
![]() $K_{\eta \boldsymbol{j}^2}(\boldsymbol{x})$
. The blue lines correspond to
$K_{\eta \boldsymbol{j}^2}(\boldsymbol{x})$
. The blue lines correspond to
![]() $K=[3/2][S^2-1]$
as mentioned before (see § 3.2).
$K=[3/2][S^2-1]$
as mentioned before (see § 3.2).
We note the following: whereas for NS turbulence, the three components of the velocity field are Gaussian with the
![]() $K(S)$
relation centered on the
$K(S)$
relation centered on the
![]() $(0,0)$
point, here, the peak in values for
$(0,0)$
point, here, the peak in values for
![]() $K$
at
$K$
at
![]() $S\approx 0$
for
$S\approx 0$
for
![]() $v_z$
is up to
$v_z$
is up to
![]() $K\approx 14$
, and rather narrowly centered around
$K\approx 14$
, and rather narrowly centered around
![]() $S_{v_z}\approx 0$
; high
$S_{v_z}\approx 0$
; high
![]() $K$
values are also present for
$K$
values are also present for
![]() $b_z$
. The hydrodynamic case analyzed in Pouquet et al. (Reference Pouquet, Rosenberg, Marino and Mininni2023) is computed at comparable
$b_z$
. The hydrodynamic case analyzed in Pouquet et al. (Reference Pouquet, Rosenberg, Marino and Mininni2023) is computed at comparable
![]() $R_\lambda$
and
$R_\lambda$
and
![]() $n_p$
(but not
$n_p$
(but not
![]() $T_{max}$
), and both
$T_{max}$
), and both
![]() $S$
and
$S$
and
![]() $K$
for the velocity are close to
$K$
for the velocity are close to
![]() $0$
. On the other hand, for stratified flows with or without rotation, the vertical component of the velocity,
$0$
. On the other hand, for stratified flows with or without rotation, the vertical component of the velocity,
![]() $v_z$
, can have high kurtosis and high values itself; this is associated with the intermittency of dissipation because of the variability of the system dominated by waves with the sudden development of small dissipative scales through shear-related instabilities. For this MHD run, the
$v_z$
, can have high kurtosis and high values itself; this is associated with the intermittency of dissipation because of the variability of the system dominated by waves with the sudden development of small dissipative scales through shear-related instabilities. For this MHD run, the
![]() $x$
and
$x$
and
![]() $y$
components of the velocity behave approximately in the same way as
$y$
components of the velocity behave approximately in the same way as
![]() $v_z$
(not shown), with a skewness comparable to that of
$v_z$
(not shown), with a skewness comparable to that of
![]() $v_z$
but smaller kurtosis.
$v_z$
but smaller kurtosis.

Figure 3. Top: for run TG3,
![]() $K(S)$
for the vertical velocity
$K(S)$
for the vertical velocity
![]() $v_z$
(left), the square vorticity density
$v_z$
(left), the square vorticity density
![]() $\boldsymbol {\omega }^2$
(middle) and the point-wise kinetic energy dissipation
$\boldsymbol {\omega }^2$
(middle) and the point-wise kinetic energy dissipation
![]() $\epsilon _v$
(right). Bottom:
$\epsilon _v$
(right). Bottom:
![]() $K(S)$
for
$K(S)$
for
![]() $b_z$
(left),
$b_z$
(left),
![]() $\sigma _m$
(middle) and
$\sigma _m$
(middle) and
![]() $\eta \boldsymbol{j}^2$
(right). The color bar at left indicates the temporal clock in units of turn-over times, with early (late) times in blue (red). The blue lines follow
$\eta \boldsymbol{j}^2$
(right). The color bar at left indicates the temporal clock in units of turn-over times, with early (late) times in blue (red). The blue lines follow
![]() $K(S)=3/2[S^2 - 1]$
.
$K(S)=3/2[S^2 - 1]$
.
The symmetric and anti-symmetric parts of both the velocity and magnetic field gradient tensors have both high skewness and high kurtosis and for them, a quasi-parabolic fit is appropriate. The magnetic dissipation has higher kurtosis and thus is likely significantly more intermittent than its kinetic counterpart, and similarly for
![]() $\sigma _m$
and vorticity. On the other hand, both kinetic and magnetic dissipations have lower skewness and kurtosis than for the other part of their gradient tensors, although their statistics overall are similar. We recall that double exponential (Laplace), or Weibull distributions have small
$\sigma _m$
and vorticity. On the other hand, both kinetic and magnetic dissipations have lower skewness and kurtosis than for the other part of their gradient tensors, although their statistics overall are similar. We recall that double exponential (Laplace), or Weibull distributions have small
![]() $S$
of either sign and high kurtosis (Bertin & Clusel (Reference Bertin and Clusel2006); Biri, Scharffenberg & Stammer Reference Biri, Scharffenberg and Stammer2015; Reference Aschwanden2016). In that context, we note that it is shown in Sorriso-Valvo et al. (Reference Sorriso-Valvo, Carbone, Perri, Greco, Marino and Bruno2018) that a proxy of energy transfer for the solar wind can be defined based on exact laws for MHD corresponding to the conservation of energy and cross-helicity
$S$
of either sign and high kurtosis (Bertin & Clusel (Reference Bertin and Clusel2006); Biri, Scharffenberg & Stammer Reference Biri, Scharffenberg and Stammer2015; Reference Aschwanden2016). In that context, we note that it is shown in Sorriso-Valvo et al. (Reference Sorriso-Valvo, Carbone, Perri, Greco, Marino and Bruno2018) that a proxy of energy transfer for the solar wind can be defined based on exact laws for MHD corresponding to the conservation of energy and cross-helicity
![]() $H_C=\left \lt \boldsymbol{v} \cdot \boldsymbol{b} \right \gt$
; these proxy fields display high intermittency in Helios 2 (and Ulysses) data, with plausible stretched exponential fits. A final remark is that data points with
$H_C=\left \lt \boldsymbol{v} \cdot \boldsymbol{b} \right \gt$
; these proxy fields display high intermittency in Helios 2 (and Ulysses) data, with plausible stretched exponential fits. A final remark is that data points with
![]() $[K,S]\approx 0$
must be dominated by random noise at these times; they could correspond to relaxation intervals following sharp bursts in energy dissipation.
$[K,S]\approx 0$
must be dominated by random noise at these times; they could correspond to relaxation intervals following sharp bursts in energy dissipation.

Figure 4. The first two rows are the same as figure 3 for run ABC2 with
![]() $R_V\approx 175$
and
$R_V\approx 175$
and
![]() $T_{max}\approx 3.14 \times 10^5$
. Bottom:
$T_{max}\approx 3.14 \times 10^5$
. Bottom:
![]() $K(S)$
is plotted for the magnetic energy
$K(S)$
is plotted for the magnetic energy
![]() $E_m$
(left) and for the symmetric part of the magnetic field gradient tensor
$E_m$
(left) and for the symmetric part of the magnetic field gradient tensor
![]() $\sigma _m$
(right), using now log–log coordinates. Approximate fits give for both
$\sigma _m$
(right), using now log–log coordinates. Approximate fits give for both
![]() $\alpha \approx 2.2, \kappa \approx 1.0$
.
$\alpha \approx 2.2, \kappa \approx 1.0$
.
We now check whether this behavior is observed as well for another type of forcing. In figure 4 are plotted the
![]() $K(S)$
relationships at the top for
$K(S)$
relationships at the top for
![]() $v_z$
(left),
$v_z$
(left),
![]() $\boldsymbol {\omega }^2$
(middle) and
$\boldsymbol {\omega }^2$
(middle) and
![]() $\epsilon _v$
(right) and (middle row),
$\epsilon _v$
(right) and (middle row),
![]() $b_z$
(left),
$b_z$
(left),
![]() $\sigma _m$
(middle) and
$\sigma _m$
(middle) and
![]() $\eta \boldsymbol{j}^2$
(right), as in figure 3 but now for run ABC2 with a fully helical ABC forcing. Values for
$\eta \boldsymbol{j}^2$
(right), as in figure 3 but now for run ABC2 with a fully helical ABC forcing. Values for
![]() $(S,K)$
for both runs are comparable except for the vertical component of the velocity due to its specific structure. We added in the last row of figure 4 the
$(S,K)$
for both runs are comparable except for the vertical component of the velocity due to its specific structure. We added in the last row of figure 4 the
![]() $K(S)$
plots for the magnetic energy (left) and
$K(S)$
plots for the magnetic energy (left) and
![]() $\sigma _m$
(right) for the same run, and using now log–log coordinates. Power laws are conspicuous above some threshold in skewness, with
$\sigma _m$
(right) for the same run, and using now log–log coordinates. Power laws are conspicuous above some threshold in skewness, with
![]() $E_m \approx 0.96S^{2.20}, \ \sigma _m \approx 0.96S^{2.25},\ \eta j^2\approx 1.05 S^{2.17}$
.
$E_m \approx 0.96S^{2.20}, \ \sigma _m \approx 0.96S^{2.25},\ \eta j^2\approx 1.05 S^{2.17}$
.
Finally, due to the strong symmetries of the initial conditions and forcing of the dynamos analyzed in this paper, one could wonder whether the addition of a small noise would change the results. On the other hand, in view of the length of the computations, well beyond what can be estimated for a reasonable Lyapounov time of separation of trajectories, it is unlikely that the overall results, and in particular the quasi-parabolic law for dissipation, would be altered. Indeed, one can find estimates of the first Lyapounov exponent
![]() $\lambda _1$
, in the ABC dynamo for example, with
$\lambda _1$
, in the ABC dynamo for example, with
![]() $\lambda _1\sim 0.073$
for a run with
$\lambda _1\sim 0.073$
for a run with
![]() $R_V\approx 60, P_M=4$
, comparable to what we have here (Zienicke, Politano & Pouquet Reference Zienicke, Politano and Pouquet1998; Alexakis & Ponty Reference Alexakis and Ponty2008), meaning that, after roughly
$R_V\approx 60, P_M=4$
, comparable to what we have here (Zienicke, Politano & Pouquet Reference Zienicke, Politano and Pouquet1998; Alexakis & Ponty Reference Alexakis and Ponty2008), meaning that, after roughly
![]() $14 \tau _{nl}$
, the initial conditions have been forgotten.
$14 \tau _{nl}$
, the initial conditions have been forgotten.
4. Kurtosis–skewness law as given by classical intermittency models
We can in fact compute the scaling exponent
![]() $\alpha _f$
in the relationship
$\alpha _f$
in the relationship
![]() $K(S)\sim S^{\alpha _f}$
, assuming the usual formulation for the structure functions of order
$K(S)\sim S^{\alpha _f}$
, assuming the usual formulation for the structure functions of order
![]() $p$
for a scalar field
$p$
for a scalar field
![]() $f$
, namely the field differences over a distance
$f$
, namely the field differences over a distance
![]() $r$
,
$r$
,
![]() $\left \lt \delta f(r)^p \right \gt \sim r^{\zeta _p}$
; one obtains for
$\left \lt \delta f(r)^p \right \gt \sim r^{\zeta _p}$
; one obtains for
![]() $\alpha _f$
$\alpha _f$
Within the framework of the standard multi-fractal She & Lévêque (Reference She and Lévêque1994) (SL) model for fluids (indicated by the index slf), and generalized for MHD in Grauer, Krug & Mariani (Reference Grauer, Krug and Mariani1994) and Politano & Pouquet (Reference Politano and Pouquet1995) (index slm), one has
 \begin{eqnarray} \zeta _p^{slf}&=& \frac {p}{9} + 2 \left [ 1 - \left ( \frac {2}{3} \right )^{p/3} \right ] \ ; \ \ \alpha _{slf} = \frac {2 [1 - 2(2/3)^{2/3} + (2/3)^{4/3}]}{7/3 - 3 (2/3)^{2/3}} \ \approx \ 2.56 \ ; \end{eqnarray}
\begin{eqnarray} \zeta _p^{slf}&=& \frac {p}{9} + 2 \left [ 1 - \left ( \frac {2}{3} \right )^{p/3} \right ] \ ; \ \ \alpha _{slf} = \frac {2 [1 - 2(2/3)^{2/3} + (2/3)^{4/3}]}{7/3 - 3 (2/3)^{2/3}} \ \approx \ 2.56 \ ; \end{eqnarray}
In building these SL models for fluid turbulence (slf) and MHD (slm), an assumption is made that a hierarchy of flux structures exists compatible with a Kolmogorov transfer time scale and with vortex filaments (or in MHD, an isotropic Iroshnikov–Kraichnan wave–eddy interaction and current sheets). This leads to a specific nonlinear relation in
![]() $p$
for the
$p$
for the
![]() $\zeta _p$
s. Note that a parabolic scaling,
$\zeta _p$
s. Note that a parabolic scaling,
![]() $\alpha =2$
is obtained when considering the generalized versions of these log-Poisson models – derived in Politano & Pouquet (Reference Politano and Pouquet1995) both for fluids and for MHD – as the intermittency becomes maximal with extreme flux structures whose geometrical signature disappears in the expression of
$\alpha =2$
is obtained when considering the generalized versions of these log-Poisson models – derived in Politano & Pouquet (Reference Politano and Pouquet1995) both for fluids and for MHD – as the intermittency becomes maximal with extreme flux structures whose geometrical signature disappears in the expression of
![]() $\alpha$
(see Pouquet et al. Reference Pouquet, Marino, Politano, Ponty and Rosenberg2025).
$\alpha$
(see Pouquet et al. Reference Pouquet, Marino, Politano, Ponty and Rosenberg2025).

Figure 5. Log–log plot for
![]() $|K|(|S|) = \kappa |S|^{\alpha }$
, runs TG3 (top) and ABC2 (bottom), for kinetic (left) and magnetic (right) dissipation. Thresholds in
$|K|(|S|) = \kappa |S|^{\alpha }$
, runs TG3 (top) and ABC2 (bottom), for kinetic (left) and magnetic (right) dissipation. Thresholds in
![]() $S$
are displayed in different colors, and similarly for the power-law fits, as indicated in each inset.
$S$
are displayed in different colors, and similarly for the power-law fits, as indicated in each inset.
In this context, we compute power-law fits,
![]() $|K| = \kappa |S|^\alpha$
, (as displayed in figures 5 and 6) for the TG3 and ABC2 runs for the kinetic and magnetic dissipations, and for both full and thresholded data. There are clear variations of
$|K| = \kappa |S|^\alpha$
, (as displayed in figures 5 and 6) for the TG3 and ABC2 runs for the kinetic and magnetic dissipations, and for both full and thresholded data. There are clear variations of
![]() $\alpha$
with the strength of the intermittency as evaluated through the level of the skewness. Specifically, the chosen thresholds are
$\alpha$
with the strength of the intermittency as evaluated through the level of the skewness. Specifically, the chosen thresholds are
![]() $S\lt 2$
(black),
$S\lt 2$
(black),
![]() $2\leqslant S \lt 3$
(blue),
$2\leqslant S \lt 3$
(blue),
![]() $3\leqslant S \lt 5$
(green) and
$3\leqslant S \lt 5$
(green) and
![]() $S\geqslant 5$
(red). Power-law fits in these intervals are given using the same colors. The high
$S\geqslant 5$
(red). Power-law fits in these intervals are given using the same colors. The high
![]() $S, K$
values reached here are related to the very long integration times allowing for a thorough exploration of configuration space. We note that the velocity field has a broad range with non-intermittent values (black dots) in the sense that both
$S, K$
values reached here are related to the very long integration times allowing for a thorough exploration of configuration space. We note that the velocity field has a broad range with non-intermittent values (black dots) in the sense that both
![]() $S$
and
$S$
and
![]() $K$
are quite low; it also undergoes a change of sign of the skewness at low values for TG3. We also observe that
$K$
are quite low; it also undergoes a change of sign of the skewness at low values for TG3. We also observe that
![]() $S$
and
$S$
and
![]() $K$
can be substantially higher for
$K$
can be substantially higher for
![]() $\eta j^2$
than for the point-wise kinetic energy dissipation, and with less scatter for
$\eta j^2$
than for the point-wise kinetic energy dissipation, and with less scatter for
![]() $K$
at a given
$K$
at a given
![]() $S$
. This difference might be related to the dynamo that controls the behavior of the magnetic field and its dissipation, whereas the velocity, at these resolutions, still feels the effect of the forcing, but the fit that includes these low-
$S$
. This difference might be related to the dynamo that controls the behavior of the magnetic field and its dissipation, whereas the velocity, at these resolutions, still feels the effect of the forcing, but the fit that includes these low-
![]() $S$
points does not represent the behavior of the more intermittent data.
$S$
points does not represent the behavior of the more intermittent data.
Skewness and excess kurtosis can be negative, which is why absolute values are used to visualize the realizations. It is important to mention that Fisher’s definition is applied here (where a normal distribution corresponds to zero), then negative values (above
![]() $-3$
) are common. For magnetic field quantities, the percentage of negative skewness (S) or kurtosis (K) is nearly zero. In contrast, the skewness of the velocity dissipation rate
$-3$
) are common. For magnetic field quantities, the percentage of negative skewness (S) or kurtosis (K) is nearly zero. In contrast, the skewness of the velocity dissipation rate
![]() $\epsilon _v$
can reach up to 2 % negative values across all realizations (thus represent only few black points in figure 5). Only in the ABC2 case, the proportion of negative and positive kurtosis values of the velocity dissipation becomes equivalent.
$\epsilon _v$
can reach up to 2 % negative values across all realizations (thus represent only few black points in figure 5). Only in the ABC2 case, the proportion of negative and positive kurtosis values of the velocity dissipation becomes equivalent.
We give some more quantitative information in figure 6, looking at variations with threshold in skewness of the power-law index
![]() $\alpha$
for the dissipation fields, namely
$\alpha$
for the dissipation fields, namely
![]() $\eta j^2$
(left) and
$\eta j^2$
(left) and
![]() $\epsilon _v$
(right) for the two ABC runs (top) and the two TG runs (bottom); these runs are identified in the inserts by line and color.
$\epsilon _v$
(right) for the two ABC runs (top) and the two TG runs (bottom); these runs are identified in the inserts by line and color.
We note first that the run TG3 has a higher
![]() $R_M$
, and the two ABC runs have higher
$R_M$
, and the two ABC runs have higher
![]() $R_\lambda$
. We also note that the overall ranges of variations for the power-law index is lesser for the TG runs than for the ABC runs, probably due to the fact that the TG run is more developed, and the effect of the forcing is lesser. The power-law index for
$R_\lambda$
. We also note that the overall ranges of variations for the power-law index is lesser for the TG runs than for the ABC runs, probably due to the fact that the TG run is more developed, and the effect of the forcing is lesser. The power-law index for
![]() $\epsilon _v$
for run ABC2 has a substantially larger range of variation than for
$\epsilon _v$
for run ABC2 has a substantially larger range of variation than for
![]() $ \eta j^2$
, with
$ \eta j^2$
, with
![]() $0^+ \lt \alpha _{\epsilon _v} \lesssim 5.0$
overall, versus
$0^+ \lt \alpha _{\epsilon _v} \lesssim 5.0$
overall, versus
![]() $1.95 \lt \alpha _{j^2} \lesssim 2.17$
. In general, rather abrupt changes in the values of
$1.95 \lt \alpha _{j^2} \lesssim 2.17$
. In general, rather abrupt changes in the values of
![]() $\alpha$
(and
$\alpha$
(and
![]() $\kappa$
, not shown) occur for
$\kappa$
, not shown) occur for
![]() $S\gtrapprox 0.5$
, i.e. when turbulent motions develop locally. For the current,
$S\gtrapprox 0.5$
, i.e. when turbulent motions develop locally. For the current,
![]() $\alpha _{\eta j^2}$
decreases systematically towards
$\alpha _{\eta j^2}$
decreases systematically towards
![]() $\alpha _{\eta j^2}\approx 2$
when the threshold in
$\alpha _{\eta j^2}\approx 2$
when the threshold in
![]() $S_{\eta j^2}$
is increased. We also note that we see a systematic decreasing trend in
$S_{\eta j^2}$
is increased. We also note that we see a systematic decreasing trend in
![]() $\alpha$
towards a value of
$\alpha$
towards a value of
![]() $2$
or slightly lower, a value that can be recovered with the extension of the SL model to more varied dissipative structures (Pouquet et al. (Reference Pouquet, Marino, Politano, Ponty and Rosenberg2025)). Finally, the constant
$2$
or slightly lower, a value that can be recovered with the extension of the SL model to more varied dissipative structures (Pouquet et al. (Reference Pouquet, Marino, Politano, Ponty and Rosenberg2025)). Finally, the constant
![]() $\kappa$
(not shown) is of order unity in all cases, and slightly increases with threshold as long as enough data are available. We also note its quasi-constancy at lower
$\kappa$
(not shown) is of order unity in all cases, and slightly increases with threshold as long as enough data are available. We also note its quasi-constancy at lower
![]() $S$
values.
$S$
values.

Figure 6. The
![]() $|K(S)|\sim \kappa |S|^\alpha$
fit: variations with filter threshold in
$|K(S)|\sim \kappa |S|^\alpha$
fit: variations with filter threshold in
![]() $S$
of
$S$
of
![]() $\alpha$
for
$\alpha$
for
![]() $\eta \boldsymbol{j}^2$
(left) and
$\eta \boldsymbol{j}^2$
(left) and
![]() $\epsilon _V$
(right) for the ABC (top) and TG (bottom) flows; runs are differentiated by their colored lines.
$\epsilon _V$
(right) for the ABC (top) and TG (bottom) flows; runs are differentiated by their colored lines.
A common feature of all these plots is that there are notable variations with threshold in
![]() $S$
, starting rather abruptly in the case of the ABC flows. This could indicate an effect on the velocity of the influence of the forcing at these moderate Reynolds numbers and that the velocity is not necessarily changed by the magnetic field which remains somewhat weak (see figures 1 and 2 and table 1). Indeed, with the ratio
$S$
, starting rather abruptly in the case of the ABC flows. This could indicate an effect on the velocity of the influence of the forcing at these moderate Reynolds numbers and that the velocity is not necessarily changed by the magnetic field which remains somewhat weak (see figures 1 and 2 and table 1). Indeed, with the ratio
![]() $r=R_M/R_M^C\approx 1^+$
for all runs except run TG3 (see table 1), we are still rather close to the threshold of the onset of the dynamo.
$r=R_M/R_M^C\approx 1^+$
for all runs except run TG3 (see table 1), we are still rather close to the threshold of the onset of the dynamo.
5. Discussion, conclusion and perspectives
We have found in this paper that, rather close to the threshold of the fast dynamo regime, a now classical quasi-parabolic behavior between kurtosis and skewness is present for kinetic and magnetic variables. The numerical data we analyzed represent but one aspect of the study of intermittency in the dynamo regime, and many questions remain. One issue concerns the effect a fully turbulent velocity will have on
![]() $K(S)$
scaling and the turbulence of the magnetic field itself. For example, using wavelets, Camporeale et al. (Reference Camporeale, Sorriso-Valvo, Califano and Retinó2018) could estimate in high-resolution 2-D DNS of Hall-MHD that only 25 % of the volume supports 50 % of the energy transfer, giving thus a quantitative estimate of the intermittency of energy dissipation; we note that, for stratified fluids, this proportion can go as low as 11 % of the kinetic energy dissipation for high kurtosis of the vertical velocity (Marino et al. Reference Marino, Feraco, Primavera, Pumir, Pouquet and Rosenberg2022). It will be of interest to examine as well these statistics in the case of fast dynamos at higher Reynolds numbers.
$K(S)$
scaling and the turbulence of the magnetic field itself. For example, using wavelets, Camporeale et al. (Reference Camporeale, Sorriso-Valvo, Califano and Retinó2018) could estimate in high-resolution 2-D DNS of Hall-MHD that only 25 % of the volume supports 50 % of the energy transfer, giving thus a quantitative estimate of the intermittency of energy dissipation; we note that, for stratified fluids, this proportion can go as low as 11 % of the kinetic energy dissipation for high kurtosis of the vertical velocity (Marino et al. Reference Marino, Feraco, Primavera, Pumir, Pouquet and Rosenberg2022). It will be of interest to examine as well these statistics in the case of fast dynamos at higher Reynolds numbers.
Another question is whether the intermittency of the early dissipation range dominates the statistics, at least at moderate Reynolds numbers. Indeed, one could argue that the intermittency of the dissipation is mostly located in the beginning of the range, due to the ensuing fast decay. In Wu et al. (Reference Wu, Huang, Wang, Yuan, He and Yang2023), a near-dissipation range intermittency is examined using solar wind data obtained with the Parker Solar Probe. The authors conclude that they find evidence for log-Poisson scaling as modeled for MHD in Grauer et al. (Reference Grauer, Krug and Mariani1994); Politano & Pouquet (Reference Politano and Pouquet1995), and that such structures are also almost entirely responsible for the intermittency anisotropy (see also Bian & Li Reference Bian and Li2024). This may be consistent with stating, as developed already in Kraichnan (Reference Kraichnan1967), that most of the intermittency is in fact at the beginning of the dissipative range.
Another issue is whether or not there is a dynamical consequence of
![]() $K(S)$
being close to its Cauchy–Schwarz limit. These inequalities linking
$K(S)$
being close to its Cauchy–Schwarz limit. These inequalities linking
![]() $K$
and
$K$
and
![]() $S$
can be viewed as a limitation both on skewness (which has to be smaller than some value) and kurtosis, which cannot be too small. It shows that non-Gaussianity and intermittency are unavoidable (except for the trivial
$S$
can be viewed as a limitation both on skewness (which has to be smaller than some value) and kurtosis, which cannot be too small. It shows that non-Gaussianity and intermittency are unavoidable (except for the trivial
![]() $(K=0,S=0)$
solution), but also that intermittency is limited in the sense that
$(K=0,S=0)$
solution), but also that intermittency is limited in the sense that
![]() $K$
and
$K$
and
![]() $S$
are not independent, and at least for the NS case, the skewness is constrained by the exact law stemming from energy conservation (Kolmogorov Reference Kolmogorov1941), the laws in MHD involving cross-correlations (see for a recent review Marino & Sorriso-Valvo Reference Marino and Sorriso-Valvo2023). Furthermore, as noted by several authors,
$S$
are not independent, and at least for the NS case, the skewness is constrained by the exact law stemming from energy conservation (Kolmogorov Reference Kolmogorov1941), the laws in MHD involving cross-correlations (see for a recent review Marino & Sorriso-Valvo Reference Marino and Sorriso-Valvo2023). Furthermore, as noted by several authors,
![]() $K(S)$
laws may put some limitation on the type of PDFs that a particular intermittent field follows. Similarly, some of these
$K(S)$
laws may put some limitation on the type of PDFs that a particular intermittent field follows. Similarly, some of these
![]() $K(S)$
relationships may contribute insight as to the relevance of large eddy simulation parametrizations by providing constraints on the flow characteristics.
$K(S)$
relationships may contribute insight as to the relevance of large eddy simulation parametrizations by providing constraints on the flow characteristics.
The role of anisotropy in interpreting the dynamics of turbulent flows is complex, including at larger
![]() $R_V$
such as that encountered in the atmosphere (Lovejoy, Schertzer & Stanway Reference Lovejoy, Schertzer and Stanway2001). For example, it is shown in Galtier (Reference Galtier2023) that it affects in different ways the amplitude of the energy distribution and the spectral indices, so more work will be needed in that direction as well; we already know that, for anisotropic fluid flows in the presence of stratification, the skewness and kurtosis of velocity components can be direction-dependent (Bos, Liechtenstein & Schneider Reference Bos, Liechtenstein and Schneider2007; see also Homann et al. Reference Homann, Ponty, Krstulovic and Grauer2014 for the fast dynamo), and that anisotropic scaling laws can be developed phenomenologically and found observationally (Nazarenko & Schekochihin Reference Nazarenko and Schekochihin2011; Bian & Li Reference Bian and Li2024).
$R_V$
such as that encountered in the atmosphere (Lovejoy, Schertzer & Stanway Reference Lovejoy, Schertzer and Stanway2001). For example, it is shown in Galtier (Reference Galtier2023) that it affects in different ways the amplitude of the energy distribution and the spectral indices, so more work will be needed in that direction as well; we already know that, for anisotropic fluid flows in the presence of stratification, the skewness and kurtosis of velocity components can be direction-dependent (Bos, Liechtenstein & Schneider Reference Bos, Liechtenstein and Schneider2007; see also Homann et al. Reference Homann, Ponty, Krstulovic and Grauer2014 for the fast dynamo), and that anisotropic scaling laws can be developed phenomenologically and found observationally (Nazarenko & Schekochihin Reference Nazarenko and Schekochihin2011; Bian & Li Reference Bian and Li2024).
When the velocity field is chaotic but not yet fully turbulent, and close to threshold for dynamo action, Sweet et al. (Reference Sweet, Ott, Antonsen, Lathrop and Finn2001) identified a temporal bursty ‘on–off’ behavior of the dynamo-generated magnetic field which grows on average linearly with the control parameter, i.e. the distance in
![]() $R_M$
from the threshold (see also Ponty et al. Reference Ponty, Laval, Dubrulle, Daviaud and Pinton2007; Alexakis & Ponty Reference Alexakis and Ponty2008, but these authors did not give indications on the behavior of the first few moments of the growing field). In Alexakis & Ponty (Reference Alexakis and Ponty2008), the Lorentz force feedback on the flow is studied in detail with DNS ran for up to
$R_M$
from the threshold (see also Ponty et al. Reference Ponty, Laval, Dubrulle, Daviaud and Pinton2007; Alexakis & Ponty Reference Alexakis and Ponty2008, but these authors did not give indications on the behavior of the first few moments of the growing field). In Alexakis & Ponty (Reference Alexakis and Ponty2008), the Lorentz force feedback on the flow is studied in detail with DNS ran for up to
![]() $10^5 \tau _{nl}$
and for various
$10^5 \tau _{nl}$
and for various
![]() $P_M$
. They find that the Lorentz force strongly modifies the temporal evolution of the growing field through a control of the noise. We already know that the noise can alter the coefficients in a parabolic relation (Theodorsen, Garcia & Rypdal Reference Theodorsen, Garcia and Rypdal2017; Losada et al. Reference Losada, Theodorsen and Garcia2023), so we might be able to observe a change of scaling once we enter a turbulent saturation regime for the dynamo at higher Reynolds numbers, as we did for stratified flows (Pouquet et al. Reference Pouquet, Rosenberg, Marino and Mininni2023). This is left for future work.
$P_M$
. They find that the Lorentz force strongly modifies the temporal evolution of the growing field through a control of the noise. We already know that the noise can alter the coefficients in a parabolic relation (Theodorsen, Garcia & Rypdal Reference Theodorsen, Garcia and Rypdal2017; Losada et al. Reference Losada, Theodorsen and Garcia2023), so we might be able to observe a change of scaling once we enter a turbulent saturation regime for the dynamo at higher Reynolds numbers, as we did for stratified flows (Pouquet et al. Reference Pouquet, Rosenberg, Marino and Mininni2023). This is left for future work.
Acknowledgements
Y.P. thanks A. Miniussi for computing design assistance on the CUBBY code. The authors are grateful to the OPAL infrastructure from Université Côte d’Azur, the Université Côte d’Azur’s Center for High-Performance Computing and to the national French computer facilities (GENCI) for providing resources and support. A.P. is thankful to Bob Ergun for his encouragement.
Editor Steve Tobias thanks the referees for their advice in evaluating this article.
Declaration of interests
The authors report no conflict of interest.