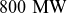1. Introduction
The success of any fusion pilot plant (FPP) requires the compatibility of the proposed core confinement scheme with an exhaust strategy that effectively performs the needed power and particle handling. In the following, analysis for a proposed magnetic island divertor system is provided for the Infinity Two FPP baseline plasma physics design (Hegna et al. Reference Hegna2025). Infinity Two is a four field-period quasi-isodynamic stellarator designed for excellent performance using stellarator optimization, high density and high magnetic field strength,
![]() $B = 9\text{ T}$
. A central element of the Infinity Two design is the requirement that the rotational transform has an edge resonance value so as to take advantage of an island divertor solution for the plasma exhaust. In the following, a justification for this design choice is articulated.
$B = 9\text{ T}$
. A central element of the Infinity Two design is the requirement that the rotational transform has an edge resonance value so as to take advantage of an island divertor solution for the plasma exhaust. In the following, a justification for this design choice is articulated.
1.1. Motivation
The divertor is an integral element in the functioning of any magnetic confinement fusion device, regulating plasma composition, density and power exhaust (König et al. Reference König2002; Mau et al. Reference Mau, Kaiser, Grossman, Raffray, Wang, Lyon, Maingi, Ku and Zarnstorff2008; Kuang et al. Reference Kuang2020). The divertor acts as part of the interface between the plasma and supporting systems. The concept for the divertor was originally proposed to reduce impurity concentration (Spitzer Reference Spitzer1958). The impurities in need of exhaust fall into two categories: first helium, generated as a byproduct of the fusion reaction and second, other higher Z impurities born from plasma wall interactions or purposely seeded. If the concentration of these impurities becomes too high in the core plasma, this can lead to an inability to attain self-sustained fusion burn conditions and a possibility of eventual radiative collapse of the plasma (Wenzel et al. Reference Wenzel2022). In addition to the concern of impurities, control of the hydrogenic fuel species densities and density ratios is important to attain and sustain fusion relevant conditions. Fusion fuel will need to be exhausted and reinjected many times before it is fused, so exhaust of fuel alongside impurities is unavoidable but can also be thought of as providing a flushing mechanism for unwanted impurities.
In a stellarator, the divertor material surfaces intercept edge magnetic field lines that are not connected to the core plasma, which is confined on nested magnetic surfaces. In the case of the island divertor examined in this paper, the edge field lines are in the magnetic field topology of an island chain. In this topology, the island x-point plays an analogous role to the poloidal x-point in a tokamak (Feng et al. Reference Feng, Sardei, Kisslinger, Grigull, McCormick and Reiter2004, Reference Feng, Kobayashi, Lunt and Reiter2011).
The field lines that intersect the divertor plates are populated with charged particles from the bulk plasma via perpendicular transport processes. These particles then mostly follow along field lines until they interact with the divertor surface. The targeted outflow of particles from the bulk plasma is neutralized either volumetrically, or upon contact with the wall. Neutral particles travel ballistically until they are ionizied or exhausted by vacuum pumps (Wenzel et al. Reference Wenzel2022). The outflow and contact of edge plasma with the wall also implies that plasma heat can be exhausted onto the divertor components. Hence, an important aspect of divertor design and operation is power exhaust, achieved through actively cooling the divertor components (Krychowiak et al. Reference Krychowiak2023).
In magnetic confinement fusion, in particular in tokamaks, it has been a challenge balancing the trade-off between plasma performance and the conditions necessary for long-term divertor survival. The highest fusion performance is usually correlated with intense heat fluxes and potentially excessive erosion of divertor surfaces. Progress on stellarator divertor development has been made through the experimental testing of several concepts on several different types of stellarators. It is believed that it is possible to combine the requirements of high core performance and benign edge-plasma interactions (and hence, long lifetimes of divertor components) by operating with divertor detachment – a state where a very high fraction of the power leaving the plasma is radiated away as photons and only a small fraction, carried by low energy plasma particles, reach the divertor. Operating stably with strong divertor detachment has been demonstrated convincingly on the stellarator Wendelstein 7-X (W7-X) (Pedersen et al. Reference Pedersen2019).
1.2. Layout of the paper
The layout of the paper is as follows. Section 2 summarizes the pertinent lessons learned from operation of other stellarator divertors and their implication to the Infinity Two design. Sections 3 and 4 provide overviews of power exhaust and particle exhaust, respectively. Section 5 gives a brief overview of the relevant edge topology of the Infinity Two FPP. In § 6, an Infinity Two island divertor design, similar to that used in W7-X, is described. Following that, § 7 presents the “large island backside divertor” (LIBD) concept, which is designed to improve the particle-exhaust efficiency beyond what has been achieved with previous stellarator divertors. Section 8 provides a discussion of the uncertainties in the design and identifies unresolved questions, some of which are proposed to be resolved in Infinity One, a stellarator currently being designed to validate the choices made for the Infinity Two FPP in a substantially smaller and faster-to-build optimized stellarator.
2. Selection of the Infinity Two divertor design
2.1. Lessons learned from the W7-X island divertor
The W7-X island divertor, conceived two decades ago (Renner et al. Reference Renner, Sharma, Kisslinger, Boscary, Grote and Schneider2004), has proven to be a large success. It has shown suitable power exhaust properties, successfully operating with heating power approaching 7 MW (Wolf et al. Reference Wolf2018). It has been shown that divertor detachment, which reduces the peak heat flux to the divertor by an order of magnitude or more, is stably attained by a variety of methods, including decreasing heating power, increasing density and increasing impurity density (Jakubowski et al. Reference Jakubowski2021). Detachment has been stably maintained for up to 110 s (Grulke et al. Reference Grulke2024), and will presumably be extended to much longer time durations in the upcoming phases of operation, as the device approaches its limit of 18 GJ of injected plasma heating energy, set by the finite reservoir of cooling water. During detached operation, the heat fluxes onto the divertor components are benign, easily an order of magnitude below the nominal engineering limit of 10 MW/m
![]() $^2$
. Even during attached operation, where the heat fluxes are the most intense, the heat fluxes were well below the technical limit of 10 MW/m
$^2$
. Even during attached operation, where the heat fluxes are the most intense, the heat fluxes were well below the technical limit of 10 MW/m
![]() $^2$
and are projected to remain below 10 MW/m
$^2$
and are projected to remain below 10 MW/m
![]() $^2$
even at the maximum designed heating power at steady state of 10 MW (Pedersen et al. Reference Pedersen2018).
$^2$
even at the maximum designed heating power at steady state of 10 MW (Pedersen et al. Reference Pedersen2018).
The results from the W7-X divertor show effective impurity screening. The divertor and baffle plates in W7-X have carbon as their primary plasma-facing component. The divertors are carbon-fiber composites and the baffles are made of fine-grain graphite (Boscary et al. Reference Boscary2011), so chemical sputtering leads to a continuous edge-plasma seeding with carbon and also oxygen (Zhang et al. Reference Zhang2019). In simulations, impurity screening is improved at reduced perpendicular transport (Winters et al. Reference Winters, Reimold, Feng, Perseo, Beurskens, Bozhenkov, Brunner, Fuchert, Koenig and Knauer2024a ). If perpendicular transport is reduced at higher magnetic field strength, the impurity screening properties in a reactor should be improved on what W7-X is already able to achieve.
An interesting and potentially very important result out of W7-X is that detachment is achieved when the plasma reaches a high radiation fraction. Detachment can be so extreme that the plasma minor radius shrinks measurably (Pedersen et al. Reference Pedersen2019), in some well-documented cases, the plasma completely recedes from all material walls (Pedersen et al. Reference Pedersen2021). For these small plasmas, all the power coming out of the plasma is dissipated as photons and charge-exchange neutrals. While this extreme version of detachment provides a very homogeneous heat-flux distribution, there is no direct contact between the charged plasma particles and the divertor and a macroscopic gap exists between the plasma and plasma-facing components, including the divertor. Therefore, this novel and extreme mode of operation does not appear to allow effective particle exhaust, and is not a suitable reactor operation mode, but it does show that stellarators can be operated with no plasma contact to the divertor with the energy being dissipated entirely by photons and neutrals (presumably charge-exhange neutrals).
Detachment stability is an ongoing research topic on W7-X (Feng et al. Reference Feng2021; Jakubowski et al. Reference Jakubowski2021). Results indicate that the ratio of perpendicular to parallel transport in the island can be a key parameter for detachment stability. Furthermore, field lines near the island O-point that do not intercept any surface can be a site of impurity condensation and can be detrimental to stability (Winters et al. Reference Winters2024b ). Further experimental data and improved simulation techniques will help determine the necessary parameters for a reactor divertor.
The results from W7-X thus give rise to optimism with regard to power handling and longevity of the plasma-facing components. A larger challenge is to ensure efficient particle exhaust. The challenge of efficient particle exhaust is a significant one for the W7-X divertor in general, not just for the extreme cases of small plasmas. For full-sized plasmas, with the majority of outflowing plasma particles arriving in the divertor region, measurements indicate an exhaust efficiency of 0.44 %–2.9 % (Wenzel et al. Reference Wenzel2022). In other words, a neutral particle will need to recycle back into the plasma, get reionized, then get redeposited in the divertor region where it neutralizes again, approximately 100 times, before it is removed from the plasma chamber. It is remarkable and encouraging that W7-X is capable of maintaining very long plasma discharges (as long as 480 s (Grulke et al. Reference Grulke2024)), clearly in a steady state with respect to particle inventory, with such a relatively poor particle-exhaust efficiency (Kremeyer et al. Reference Kremeyer2022).
Another challenge of the W7-X divertor was the elimination of error fields, specifically the low-order error modes with
![]() $n/m = 1$
which can perturb the island structure (Lazerson et al. Reference Lazerson2018; Bozhenkov et al. Reference Bozhenkov, Otte, Biedermann, Jakubowski, Lazerson, Sunn Pedersen and Wolf2018). Here nis the toroidal mode number and m is the poloidal mode number. These error fields were successfully eliminated, but required additional correction coils. In a pilot plant, it is desirable to limit the number of auxiliary coils that are necessary.
$n/m = 1$
which can perturb the island structure (Lazerson et al. Reference Lazerson2018; Bozhenkov et al. Reference Bozhenkov, Otte, Biedermann, Jakubowski, Lazerson, Sunn Pedersen and Wolf2018). Here nis the toroidal mode number and m is the poloidal mode number. These error fields were successfully eliminated, but required additional correction coils. In a pilot plant, it is desirable to limit the number of auxiliary coils that are necessary.
2.2. Lessons learned from other stellarator divertors
Stellarator research has employed a variety of divertor concepts in addition to the island divertor concept. In the Large Helical Device (LHD) where the dominant magnetic field is generated by helical coils, a helical divertor is employed (Ohyabu et al. Reference Ohyabu1994). This divertor looks similar to a double null tokamak divertor that rotates around the device poloidally. This divertor is attractive due to the possibility of closing the divertor, which prevents neutrals from escaping back into the plasma (Masuzaki et al. Reference Masuzaki, Shoji, Tokitani, Murase, Kobayashi, Morisaki, Yonezu, Sakamoto, Yamada and Komori2010). However, it has several serious drawbacks. The most obvious drawback is that the divertor requires large helical coils, which significantly complicate the engineering challenges. A second concern with the LHD divertor is that a large stochastic region exists between the core plasma and the divertor legs. The plasma tends to lose its momentum to cross-field transport in that region which reduces the exhaust efficiency of the divertor (Feng et al. Reference Feng2008). Finally, LHD has been experimentally unable to reach stable detachment unless a fairly large 1/1 island is introduced with external coils (Kobayashi et al. Reference Kobayashi2019).
A different divertor attempted in LHD was the local island divertor (LID) (Morisaki et al. Reference Morisaki, Masuzaki, Suzuki, Komori, Ohyabu, Motojima, Okamura and Matsuoka2003, Reference Morisaki2005). In the LID, a large 1/1 magnetic island was generated with resonant magnetic perturbation coils. A structure was inserted into the island such that particles would flow around the island separatrix and impact the back side of the structure. The LID showed success in achieving acceptable heat fluxes into the desired region. The LID also reported an improvement in the pumping efficiency over the helical divertor by approximately a factor of 4 (Masuzaki et al. Reference Masuzaki2007). However, the LID was discontinued and the amount of experimental data is limited.
Another concept considered for power plant designs is the non-resonant divertor (Boozer Reference Boozer2015; Bader et al. Reference Bader, Boozer, Hegna, Lazerson and Schmitt2017). This divertor does not use a large magnetic resonance, but instead employs a stochastic region between the last closed flux surface and the wall. There has been significant theoretical work on this concept, but very little experimental work (Punjabi & Boozer Reference Punjabi and Boozer2020; Garcia et al. Reference Garcia, Bader, Frerichs, Hartwell, Schmitt, Allen and Schmitz2023, Reference Garcia, Bader, Boeyaert, Boozer, Frerichs, Gerard, Punjabi and Schmitz2024). Of specific concern are the possible momentum losses in the edge, stable operation including high radiative fractions necessary for the survival of divertor components, and the exhaust efficiency of helium ash.
2.3. Implications for the Infinity Two divertor
In evaluating the alternative divertor concepts, we decided that only the island divertor concept was sufficiently far enough advanced to be used in the Infinity Two FPP. The requirement for modular coils outside a blanket eliminates the possibility of a helical divertor. The lack of experimental results makes the application of a non-resonant divertor too risky. In contrast, the island divertor has already demonstrated the necessary power exhaust properties, but needs some improvement with regard to particle exhaust.
The selection of an island divertor included some high level design choices for Infinity Two. We required an iota profile that generated a suitable edge island. Furthermore, we chose an edge island chain that was not resonant at the
![]() $\iota$
= 1 surface, to avoid the issue of low-order error modes. Here
$\iota$
= 1 surface, to avoid the issue of low-order error modes. Here
![]() $\iota$
represents the rotational transform.
$\iota$
represents the rotational transform.
The decision to employ an island divertor also influenced the choice of stellarator type. The quasi-isodynamic stellarator can be optimized for very low bootstrap current and is well suited to an island divertor with an edge resonance.
2.4. Parameters of Infinity Two
Infinity Two is a four field-period quasi-isodynamic configuration, with a major radius of 12.5 m, and a magnetic field of 9 T. The parameters of the device are given in table 1. As described below, the rotational transform and coil set have been chosen to produce a substantial island chain at the plasma edge, suitable for an island divertor. The nominal operating point for Infinity Two is 800 MW Deuterium-tritium (DT) fusion power, which gives a total of 160 MW of plasma heating due to alpha particles. The baseline scenario of Infinity Two includes 20 MW of auxiliary power.
Table 1. Operational parameters of the stellarator power plant.

3. Power exhaust in a stellarator pilot plant
In table 2 we provide some of the features and requirements of the Infinity Two divertor. The full connection length (
![]() $L_c$
) is calculated by following a field line close to the island separatrix and determining the length until it has made one full revolution around the island. The requirements on the heat load and temperature are set by material properties. In this paper we discuss the heat load requirement but are not able to calculate the temperature at the divertor at this time. The temperature requirement comes from Stangeby (Reference Stangeby2018). The angle of incidence with respect to the magnetic field is constructed by design to be 3
$L_c$
) is calculated by following a field line close to the island separatrix and determining the length until it has made one full revolution around the island. The requirements on the heat load and temperature are set by material properties. In this paper we discuss the heat load requirement but are not able to calculate the temperature at the divertor at this time. The temperature requirement comes from Stangeby (Reference Stangeby2018). The angle of incidence with respect to the magnetic field is constructed by design to be 3
![]() $^\circ$
. The value of the resonant field,
$^\circ$
. The value of the resonant field,
![]() $b_{54}$
, is calculated using equation (3.1) (Boozer Reference Boozer2004)
$b_{54}$
, is calculated using equation (3.1) (Boozer Reference Boozer2004)
From the value of
![]() $b_{54}$
it is possible to calculate the island half-width at a given location, by using
$b_{54}$
it is possible to calculate the island half-width at a given location, by using
Table 2. Features and requirements of the Infinity Two divertor.

 \begin{equation} \delta _{54} (m) = \frac {1}{\left | \nabla \psi _t \right |} \sqrt {\frac { 4 b_{54}}{5 \frac {{\rm d} \iota \left ( \psi _t \right)}{{\rm d} \psi _t}}}. \end{equation}
\begin{equation} \delta _{54} (m) = \frac {1}{\left | \nabla \psi _t \right |} \sqrt {\frac { 4 b_{54}}{5 \frac {{\rm d} \iota \left ( \psi _t \right)}{{\rm d} \psi _t}}}. \end{equation}
For the Infinity Two equilibria, the island width ranges from approximately 10 cm in the most radially compressed region (the inboard side at the
![]() $\phi = 0$
plane) to approximately 44 cm at the most radially extended (the outboard side at the half-period)
$\phi = 0$
plane) to approximately 44 cm at the most radially extended (the outboard side at the half-period)
While this paper does not represent an engineering design for a divertor, one candidate for the divertor material would be tungsten. We also do not attempt to determine the full physics of radiation control, but it is likely that impurity seeding for radiation control is necessary, with neon being a candidate impurity species.
3.1. Estimating required radiation fraction
In this section we will provide estimates for the necessary radiation fraction for a machine on the scale of Infinity Two. The actual values of the radiation fraction will depend on the physical design of the divertor, some parameters of the magnetic fields structure, and properties of the edge plasma. The radiation fraction estimate will be revised when we discuss the physical divertor performance in §§ 6 and 7.
The physics of the edge plasma in fusion devices is governed by many processes, including transport along plasma field lines, cross-field transport from turbulence or blobs, and interactions with neutrals and impurities such as de-excitation and recombination radiation, line radiation and charge-exchange processes. Furthermore, stellarators can often contain complicated magnetic geometries including stochastic regions. However, the island divertor geometry produces an edge that behaves ostensibly like a multi-null tokamak, where the island x-point plays the role of the poloidal null in a tokamak divertor (Feng et al. Reference Feng, Kobayashi, Lunt and Reiter2011).
A key parameter characterizing the plasma edge is the characteristic exponential fall-off length of the heat flux in the scrape-off layer (SOL) perpendicular to the flux surfaces, denoted by
![]() $\lambda _{q,\perp }$
. In practice, we are most concerned with the heat flux on the target. We will also define a characteristic length
$\lambda _{q,\perp }$
. In practice, we are most concerned with the heat flux on the target. We will also define a characteristic length
![]() $\lambda _{q,t}$
which represents the heat-flux spreading on the divertor plate. In this paper we will use a poloidal-like measurement for
$\lambda _{q,t}$
which represents the heat-flux spreading on the divertor plate. In this paper we will use a poloidal-like measurement for
![]() $\lambda _{q,t}$
as is done in Niemann et al. (Reference Niemann2020). A third estimate in the literature that is commonly used in tokamaks is
$\lambda _{q,t}$
as is done in Niemann et al. (Reference Niemann2020). A third estimate in the literature that is commonly used in tokamaks is
![]() $\lambda _{q,u}$
, which is the perpendicular heat flux measured at an upstream location, often the outboard midplane. Typically
$\lambda _{q,u}$
, which is the perpendicular heat flux measured at an upstream location, often the outboard midplane. Typically
![]() $\lambda _{q,u} \leq \lambda _{q,\perp } \lt \lambda _{q,t}$
. If connection lengths are long between the upstream location and the downstream location, diffusive processes can expand the heat flux. Heat flux can also be spread onto the divertor plates by tilting the divertor plates to increase area, or by magnetic flux expansion.
$\lambda _{q,u} \leq \lambda _{q,\perp } \lt \lambda _{q,t}$
. If connection lengths are long between the upstream location and the downstream location, diffusive processes can expand the heat flux. Heat flux can also be spread onto the divertor plates by tilting the divertor plates to increase area, or by magnetic flux expansion.
Using these definitions, the wetted area of the plasma can be estimated as
![]() $\lambda _{q,t} L_{\text{div}}$
, where
$\lambda _{q,t} L_{\text{div}}$
, where
![]() $L_{\text{div}}$
is the total (approximately toroidal) length of the strike lines on the divertor structures. To get a lower bound of the radiation fraction we assume an optimistic wetted area by using
$L_{\text{div}}$
is the total (approximately toroidal) length of the strike lines on the divertor structures. To get a lower bound of the radiation fraction we assume an optimistic wetted area by using
![]() $L_{\text{div}} = 2\pi R_0$
, with
$L_{\text{div}} = 2\pi R_0$
, with
![]() $R_0$
being the major radius of Infinity Two (12.5 m). If the maximum allowable heat flux per area is
$R_0$
being the major radius of Infinity Two (12.5 m). If the maximum allowable heat flux per area is
![]() $\Gamma _{\text{max}}$
and the total heat flux impacting the divertor surfaces is the alpha heating power plus the auxiliary power multiplied by the fraction that is not radiated,
$\Gamma _{\text{max}}$
and the total heat flux impacting the divertor surfaces is the alpha heating power plus the auxiliary power multiplied by the fraction that is not radiated,
![]() $Q_{\text{tot}}\left (1-f_{\text{rad}}\right)$
then the following relationship holds:
$Q_{\text{tot}}\left (1-f_{\text{rad}}\right)$
then the following relationship holds:
Using a common engineering limit of 10 MW/m
![]() $^2$
for
$^2$
for
![]() $\Gamma _{\text{max}}$
and the information for Infinity Two from table 1 the relationship between between
$\Gamma _{\text{max}}$
and the information for Infinity Two from table 1 the relationship between between
![]() $f_{\text{rad}}$
and
$f_{\text{rad}}$
and
![]() $\lambda _{q,t}$
plotted in figure 1 is given by
$\lambda _{q,t}$
plotted in figure 1 is given by

Figure 1. The required radiation fraction as a function of target heat-flux width. The expected region from extrapolation from W7-X results (§ 3.2) is shown in blue. Points representing
![]() $\lambda _{q,t}$
from the field-line following results for the classical divertor and LIBD are shown in red circles and green stars, respectively.
$\lambda _{q,t}$
from the field-line following results for the classical divertor and LIBD are shown in red circles and green stars, respectively.
This estimate assumes an even distribution of heat flux over the divertor region. The shaded region represents the range of heat-flux widths calculated in § 3.2. In addition, several points on the curve are shown corresponding to the estimated results from field-line following. The value for the LIBD (§ 7) is shown with a green star, while the results for the classical divertor (§ 6) are shown in red circles. Nevertheless, even with the optimistic assumptions, it is clear that if
![]() $\lambda _q$
is of the order of a few cm or smaller, then the radiation fraction will need to be 90 % or greater. The OP2.1 campaign in W7-X showed that stable detachment with above 90
$\lambda _q$
is of the order of a few cm or smaller, then the radiation fraction will need to be 90 % or greater. The OP2.1 campaign in W7-X showed that stable detachment with above 90
![]() $\,\%$
radiation fraction could be achieved in the Standard configuration in W7-X (Peterson et al. Reference Peterson2025; Winters et al. Reference Winters2024b
). It is hoped that future experiments on W7-X will help determine whether operation at very high radiation fraction is possible without negative effects on the core plasma.
$\,\%$
radiation fraction could be achieved in the Standard configuration in W7-X (Peterson et al. Reference Peterson2025; Winters et al. Reference Winters2024b
). It is hoped that future experiments on W7-X will help determine whether operation at very high radiation fraction is possible without negative effects on the core plasma.
3.2. Empirical estimates of heat-flux width
There is a robust and detailed body of work on the heat-flux width in tokamaks. While the tokamak edge and the stellarator edge contain fundamental differences, there are some significant parallels between the tokamak divertor and the island divertor. The heat-flux width is generally understood to be set by the combination of parallel transport, taking plasma along open field lines to the plasma targets, and perpendicular transport, transporting the plasma deeper into the SOL. The primary differences are in the topology of those SOL magnetic field lines. It is noteworthy that low-shear stellarators tend to have much longer parallel connection lengths than tokamaks (Feng et al. Reference Feng, Kobayashi, Lunt and Reiter2011). In the following, we discuss tokamak heat-flux widths in the context of connection length, and compare these with stellarator results, in an attempt to quantify, as well as possible, the heat-flux width expected in the Infinity Two SOL.
A prominent estimate of
![]() $\lambda _{q,\perp }$
from tokamaks is the Eich scaling (Eich et al. Reference Eich2013). In this scaling,
$\lambda _{q,\perp }$
from tokamaks is the Eich scaling (Eich et al. Reference Eich2013). In this scaling,
![]() $\lambda _{q,u}$
is roughly proportional to
$\lambda _{q,u}$
is roughly proportional to
![]() $q_{95} B_t^{-0.8}$
where
$q_{95} B_t^{-0.8}$
where
![]() $q_{95}$
is the edge safety factor and
$q_{95}$
is the edge safety factor and
![]() $B_t$
is the toroidal field. Here, the value of
$B_t$
is the toroidal field. Here, the value of
![]() $\lambda _{q,u}$
is measured at the upstream position at the outboard midplane;
$\lambda _{q,u}$
is measured at the upstream position at the outboard midplane;
![]() $\lambda _{q,u}$
scales approximately as the edge poloidal field. It is only weakly dependent on the power that goes into the edge. For tokamaks, the Eich scaling yields upstream heat-flux widths of 1 mm on ITER.
$\lambda _{q,u}$
scales approximately as the edge poloidal field. It is only weakly dependent on the power that goes into the edge. For tokamaks, the Eich scaling yields upstream heat-flux widths of 1 mm on ITER.
Goldston’s heuristic model (Goldston Reference Goldston2011) assumes that the magnetic
![]() $\nabla$
B and curvature drifts carry the charged particles across the last closed magnetic surface onto the open field lines in the SOL, and similar to Eich’s scaling shows an inverse proportionality between
$\nabla$
B and curvature drifts carry the charged particles across the last closed magnetic surface onto the open field lines in the SOL, and similar to Eich’s scaling shows an inverse proportionality between
![]() $\lambda _{q,u}$
and
$\lambda _{q,u}$
and
![]() $B_p$
where
$B_p$
where
![]() $B_{p}$
is the poloidal field. Goldston’s model assumes at its outset that
$B_{p}$
is the poloidal field. Goldston’s model assumes at its outset that
![]() $\lambda _q$
is fundamentally tied to the free streaming of the particles along the magnetic field from upstream to the target – a distance equal to the parallel connection length. While this leads to a
$\lambda _q$
is fundamentally tied to the free streaming of the particles along the magnetic field from upstream to the target – a distance equal to the parallel connection length. While this leads to a
![]() $\lambda _{q,\perp }$
scaling inversely proportional to
$\lambda _{q,\perp }$
scaling inversely proportional to
![]() $B_p$
in a tokamak, the connection length is not dependent on
$B_p$
in a tokamak, the connection length is not dependent on
![]() $B_p$
in a stellarator island divertor.
$B_p$
in a stellarator island divertor.
The above tokamak results are valid for H-mode plasmas. For L-mode tokamak plasmas the following empirical scaling is found (Brunner et al. Reference Brunner, LaBombard, Kuang and Terry2018):
with
![]() $p$
being the plasma pressure measured in atmospheres. Brunner also shows that, in tokamaks, L- and H-mode plasmas scale similarly, but with a different pre-factor. A study (Ahn, Counsell & Kirk Reference Ahn, Counsell and Kirk2006) performed to determine L-mode SOL width scaling in the MAST spherical tokamak shows strong dependence on safety factor and line averaged density (
$p$
being the plasma pressure measured in atmospheres. Brunner also shows that, in tokamaks, L- and H-mode plasmas scale similarly, but with a different pre-factor. A study (Ahn, Counsell & Kirk Reference Ahn, Counsell and Kirk2006) performed to determine L-mode SOL width scaling in the MAST spherical tokamak shows strong dependence on safety factor and line averaged density (
![]() $\propto$
$\propto$
![]() $q_{95}^{1.45 \pm 0.51}$
$q_{95}^{1.45 \pm 0.51}$
![]() $n_{e}^{1.45 \pm 0.17}$
). Another study (Sieglin et al. Reference Sieglin, Eich, Faitsch, Herrmann and Scarabosio2016) to investigate the divertor heat load in ASDEX Upgrade L-mode discharges in the presence of external magnetic perturbation showed behavior similar to Eich’s scaling with a key dependency on toroidal magnetic field and safety factor(
$n_{e}^{1.45 \pm 0.17}$
). Another study (Sieglin et al. Reference Sieglin, Eich, Faitsch, Herrmann and Scarabosio2016) to investigate the divertor heat load in ASDEX Upgrade L-mode discharges in the presence of external magnetic perturbation showed behavior similar to Eich’s scaling with a key dependency on toroidal magnetic field and safety factor(
![]() $\propto$
$\propto$
![]() $q_{cyl}^{1.07 \pm 0.07}$
$q_{cyl}^{1.07 \pm 0.07}$
![]() $B_{t}^{-0.78}$
).
$B_{t}^{-0.78}$
).
One of the key differences between a stellarator island divertor and a tokamak divertor is the magnitude of the edge connection length,
![]() $L_c$
, which can be significantly longer in stellarators compared with equivalently sized tokamaks (Feng et al. Reference Feng, Sardei, Grigull, McCormick, Kisslinger and Reiter2006, Reference Feng, Kobayashi, Lunt and Reiter2011). The main reason for this difference in magnitude of
$L_c$
, which can be significantly longer in stellarators compared with equivalently sized tokamaks (Feng et al. Reference Feng, Sardei, Grigull, McCormick, Kisslinger and Reiter2006, Reference Feng, Kobayashi, Lunt and Reiter2011). The main reason for this difference in magnitude of
![]() $L_c$
is that, in tokamaks, the rotational transform provides the pitch of the magnetic field relative to the toroidal direction – the direction that the tokamak divertor is aligned with – and is therefore responsible for guiding the particles and heat towards the target. In contrast, in island divertors, this role is taken up by the internal rotational transform of the magnetic island chain itself, or in other words, how quickly the magnetic field line rotates around the O-point of the island as it meanders around on an island surface. This internal transform is approximately the product of the radial size of the island and the magnetic shear at the location of the island chain. Therefore, in low-shear stellarators like W7-X,
$L_c$
is that, in tokamaks, the rotational transform provides the pitch of the magnetic field relative to the toroidal direction – the direction that the tokamak divertor is aligned with – and is therefore responsible for guiding the particles and heat towards the target. In contrast, in island divertors, this role is taken up by the internal rotational transform of the magnetic island chain itself, or in other words, how quickly the magnetic field line rotates around the O-point of the island as it meanders around on an island surface. This internal transform is approximately the product of the radial size of the island and the magnetic shear at the location of the island chain. Therefore, in low-shear stellarators like W7-X,
![]() $L_c$
can be extremely long (Sinha et al. Reference Sinha, Hölbe, Pedersen and Bozhenkov2017). This fact may limit the applicability of the tokamak models which attempt to describe the upstream heat flux,
$L_c$
can be extremely long (Sinha et al. Reference Sinha, Hölbe, Pedersen and Bozhenkov2017). This fact may limit the applicability of the tokamak models which attempt to describe the upstream heat flux,
![]() $\lambda _{q,u}$
.
$\lambda _{q,u}$
.
The relationship between
![]() $\lambda _{q,u}$
,
$\lambda _{q,u}$
,
![]() $\lambda _{q,\perp }$
and
$\lambda _{q,\perp }$
and
![]() $L_c$
in stellarator divertors is unclear. Several studies on W7-X (Gao et al. Reference Gao2019, Reference Gao2024) analyzing the effect of beta and toroidal current on the heat load on the divertor suggest that the connection length at the edge plays an important role in determining the width of the strikeline. Furthermore, results from Killer et al. (Reference Killer2019) show measurements of the upstream heat flux on W7-X showing that there is an expansion of the heat-flux width from the upstream to the downstream by roughly a factor of 4. This expansion in the edge may have dependence on plasma properties such as power and magnetic field that are different from the dependences that set the upstream width.
$L_c$
in stellarator divertors is unclear. Several studies on W7-X (Gao et al. Reference Gao2019, Reference Gao2024) analyzing the effect of beta and toroidal current on the heat load on the divertor suggest that the connection length at the edge plays an important role in determining the width of the strikeline. Furthermore, results from Killer et al. (Reference Killer2019) show measurements of the upstream heat flux on W7-X showing that there is an expansion of the heat-flux width from the upstream to the downstream by roughly a factor of 4. This expansion in the edge may have dependence on plasma properties such as power and magnetic field that are different from the dependences that set the upstream width.
Results from the experiments referenced above do not show a clear relationship between
![]() $\lambda _{q,\perp }$
and
$\lambda _{q,\perp }$
and
![]() $L_c$
. If heat-flux spreading is mainly diffusive, one would expect that
$L_c$
. If heat-flux spreading is mainly diffusive, one would expect that
![]() $\lambda _{q,\perp } \propto \sqrt {L_c}$
. This simple diffusive model is used in the field-line following calculations presented in this paper. Furthermore, results from the limiter experiments on W7-X show an even weaker dependence of
$\lambda _{q,\perp } \propto \sqrt {L_c}$
. This simple diffusive model is used in the field-line following calculations presented in this paper. Furthermore, results from the limiter experiments on W7-X show an even weaker dependence of
![]() $\lambda _{q,\perp }$
on connection length – results from Niemann et al. (Reference Niemann2019) show that
$\lambda _{q,\perp }$
on connection length – results from Niemann et al. (Reference Niemann2019) show that
![]() $\lambda _{q,\perp } \propto L_c^{0.22}$
.
$\lambda _{q,\perp } \propto L_c^{0.22}$
.
Additionally, there is an expectation of
![]() $\lambda _{q,u}$
scaling inversely with the magnetic field strength. As mentioned above, in the Eich scaling and Goldston’s drift model both scale roughly like
$\lambda _{q,u}$
scaling inversely with the magnetic field strength. As mentioned above, in the Eich scaling and Goldston’s drift model both scale roughly like
![]() $1/B_p$
. Given the safety-factor restrictions in tokamaks, and the need for a large
$1/B_p$
. Given the safety-factor restrictions in tokamaks, and the need for a large
![]() $B_p$
to ensure good energy confinement, the relationship in a tokamak between
$B_p$
to ensure good energy confinement, the relationship in a tokamak between
![]() $B$
and
$B$
and
![]() $B_p$
is not arbitrary. Hence,
$B_p$
is not arbitrary. Hence,
![]() $\lambda _{q,u}$
may ultimately scale as
$\lambda _{q,u}$
may ultimately scale as
![]() $1/B$
in a tokamak.
$1/B$
in a tokamak.
Turbulent transport scaling arguments also suggest
![]() $\lambda _{q,\perp }$
decreases with higher magnetic field. Assuming that
$\lambda _{q,\perp }$
decreases with higher magnetic field. Assuming that
![]() $\lambda _{q,\perp }$
scales roughly as the inverse square root of the cross-field heat diffusivity produces the scaling
$\lambda _{q,\perp }$
scales roughly as the inverse square root of the cross-field heat diffusivity produces the scaling
![]() $\lambda _{q,\perp } \sim \lambda _{q,t}/B$
for gyro-Bohm-like turbulence. A study (Xu et al. Reference Xu, Li, Li, Chen, Xia, Tang, Zhu and Chan2019) based on the simulations of the tokamak boundary plasma turbulence transport predicts the transition from a drift-dominant regime in current machines to a turbulence-dominant regime in future machines. Experimental results from W7-X will help to clarify the role of turbulent transport in island divertors (Jakubowski et al. Reference Jakubowski2024).
$\lambda _{q,\perp } \sim \lambda _{q,t}/B$
for gyro-Bohm-like turbulence. A study (Xu et al. Reference Xu, Li, Li, Chen, Xia, Tang, Zhu and Chan2019) based on the simulations of the tokamak boundary plasma turbulence transport predicts the transition from a drift-dominant regime in current machines to a turbulence-dominant regime in future machines. Experimental results from W7-X will help to clarify the role of turbulent transport in island divertors (Jakubowski et al. Reference Jakubowski2024).
At the time of writing, W7-X has only operated at or very close to B = 2.5 T on axis, so any dependence of
![]() $\lambda _{q,\perp }$
on the magnetic field strength in the island divertor of W7-X is not yet known. Complicating matters is that W7-X results are almost always reported on the divertor plate, that is
$\lambda _{q,\perp }$
on the magnetic field strength in the island divertor of W7-X is not yet known. Complicating matters is that W7-X results are almost always reported on the divertor plate, that is
![]() $\lambda _{q,t}$
and not
$\lambda _{q,t}$
and not
![]() $\lambda _{q,\perp }$
.
$\lambda _{q,\perp }$
.
Based on these somewhat disparate scalings we now attempt to bracket the range of estimates for
![]() $\lambda _{q,t}$
in Infinity Two with characteristic connection lengths of
$\lambda _{q,t}$
in Infinity Two with characteristic connection lengths of
![]() $\sim$
1000 m and magnetic field strength of 9 T. We assume that
$\sim$
1000 m and magnetic field strength of 9 T. We assume that
where
![]() $\alpha$
is between 0.22 and 1. The upper limit of 1 for
$\alpha$
is between 0.22 and 1. The upper limit of 1 for
![]() $\alpha$
comes from a comparison high-iota and low-iota cases on W7-X using extreme values of the ranges (Jakubowski et al. Reference Jakubowski2021; Killer et al. Reference Killer2019).
$\alpha$
comes from a comparison high-iota and low-iota cases on W7-X using extreme values of the ranges (Jakubowski et al. Reference Jakubowski2021; Killer et al. Reference Killer2019).
We scale using W7-X data where
![]() $\lambda _{q,t} \approx 5$
cm (Niemann et al. Reference Niemann2020) and
$\lambda _{q,t} \approx 5$
cm (Niemann et al. Reference Niemann2020) and
![]() $L_c \approx 250$
m (Sinha et al. Reference Sinha, Hölbe, Pedersen and Bozhenkov2017). We estimate
$L_c \approx 250$
m (Sinha et al. Reference Sinha, Hölbe, Pedersen and Bozhenkov2017). We estimate
![]() $\lambda _{q,t}$
for W7-X by adjusting with respect to the poloidal angle that the field lines make with the divertor plate. This value is not quoted anywhere unfortunately, but from published figures it appears that the angle is somewhere around 35
$\lambda _{q,t}$
for W7-X by adjusting with respect to the poloidal angle that the field lines make with the divertor plate. This value is not quoted anywhere unfortunately, but from published figures it appears that the angle is somewhere around 35
![]() $^\circ$
, giving an approximation of
$^\circ$
, giving an approximation of
![]() $\lambda _{q,\perp }$
of 4 cm.
$\lambda _{q,\perp }$
of 4 cm.
The maximal expected values of
![]() $\lambda _{q,\perp }$
for Infinity Two can be obtained assuming
$\lambda _{q,\perp }$
for Infinity Two can be obtained assuming
![]() $\alpha$
= 1 in equation (3.6). In this case
$\alpha$
= 1 in equation (3.6). In this case
![]() $\lambda _{q,\perp }$
would be expected to be 4.4 cm in Infinity Two, very similar to that seen on W7-X. On the other extreme, assuming
$\lambda _{q,\perp }$
would be expected to be 4.4 cm in Infinity Two, very similar to that seen on W7-X. On the other extreme, assuming
![]() $\alpha$
= 0.22,
$\alpha$
= 0.22,
![]() $\lambda _{q,\perp }$
would be expected to be about 1.5 cm. These two extremes show that there is about a factor of 3 in the uncertainty of
$\lambda _{q,\perp }$
would be expected to be about 1.5 cm. These two extremes show that there is about a factor of 3 in the uncertainty of
![]() $\lambda _{q,\perp }$
.
$\lambda _{q,\perp }$
.
Adding to this uncertainty is the issue of whether the power entering into the SOL from the core plasma affects
![]() $\lambda _{q,u}$
and hence
$\lambda _{q,u}$
and hence
![]() $\lambda _{q,t}$
. While the Eich scaling implies that the tokamak
$\lambda _{q,t}$
. While the Eich scaling implies that the tokamak
![]() $\lambda _{q,u}$
does not depend on this quantity, there are initial indications from W7-X that the wetted area increases with heating power (Jakubowski et al. Reference Jakubowski2021).
$\lambda _{q,u}$
does not depend on this quantity, there are initial indications from W7-X that the wetted area increases with heating power (Jakubowski et al. Reference Jakubowski2021).
In summary, the empirical and theoretical estimates of
![]() $\lambda _{q,\perp }$
and
$\lambda _{q,\perp }$
and
![]() $\lambda _{q,t}$
show substantial differences and hence point to uncertainties when extrapolating to a power plant, whose physical size,
$\lambda _{q,t}$
show substantial differences and hence point to uncertainties when extrapolating to a power plant, whose physical size,
![]() $L_c$
,
$L_c$
,
![]() $B$
, and other parameters are going to be substantially different from existing stellarators. Therefore, it would be advantageous to gain more experimental data. While some of these may come from further operation of W7-X, it will be advantageous to have further experimental data and validation in a device operating with parameters that differ from W7-X. This is further motivation for pursuing the construction and operation of an advanced test-bed stellarator.
$B$
, and other parameters are going to be substantially different from existing stellarators. Therefore, it would be advantageous to gain more experimental data. While some of these may come from further operation of W7-X, it will be advantageous to have further experimental data and validation in a device operating with parameters that differ from W7-X. This is further motivation for pursuing the construction and operation of an advanced test-bed stellarator.
4. Particle exhaust in Infinity Two
In addition to exhausting the heat flux from the plasma, it is necessary to also exhaust the particles. Without adequate control of the particle exhaust, there will be a build-up of helium ash in the plasma.
An FPP producing 800 MW of fusion power will produce 2.8
![]() $\times$
10
$\times$
10
![]() $^{20}$
alpha particles per second. Assuming a 5 % helium concentration in the plasma, and also assuming that the helium is exhausted at the same rate as the bulk plasma, the pilot plant will need to exhaust at least 5.6
$^{20}$
alpha particles per second. Assuming a 5 % helium concentration in the plasma, and also assuming that the helium is exhausted at the same rate as the bulk plasma, the pilot plant will need to exhaust at least 5.6
![]() $\times$
10
$\times$
10
![]() $^{21}$
particles per second. The exhausted plasma is balanced by core fueling from pellets. In Infinity Two, the pellet fueling is also used to control the density profiles, and this requirement sets a higher requirement on the exhausted particles, at 2.2
$^{21}$
particles per second. The exhausted plasma is balanced by core fueling from pellets. In Infinity Two, the pellet fueling is also used to control the density profiles, and this requirement sets a higher requirement on the exhausted particles, at 2.2
![]() $\times$
10
$\times$
10
![]() $^{22}$
particles per second (Guttenfelder et al. Reference Guttenfelder2025). This is an increase of the particle-exhaust requirement over what is need to remove the helium ash, but also allows for a lower ratio of the helium to the hydrogenic species in the exhaust than is found in the bulk plasma. We use the estimate of 2.2
$^{22}$
particles per second (Guttenfelder et al. Reference Guttenfelder2025). This is an increase of the particle-exhaust requirement over what is need to remove the helium ash, but also allows for a lower ratio of the helium to the hydrogenic species in the exhaust than is found in the bulk plasma. We use the estimate of 2.2
![]() $\times$
10
$\times$
10
![]() $^{22}$
particles per second for the exhaust rate in the analysis in this section.
$^{22}$
particles per second for the exhaust rate in the analysis in this section.
We estimate the required pumping efficiency necessary to achieve stationary conditions in such a pilot plant. This estimate can be accomplished based on constraints on the plasma in contact with the divertor material surface, primarily the maximum allowable heat flux and plasma temperature which are set by engineering limits on heat removal and the need to minimize erosion of the surface. Stellarators may have an additional constraint, which is a limit on the maximum achievable divertor plasma density: to date stellarators have not demonstrated a strong high-recycling regime in the divertor with
![]() $n_{\text{div}}\gg n_{\text{sep}}$
, as discussed below.
$n_{\text{div}}\gg n_{\text{sep}}$
, as discussed below.
In order to account for this possible limitation, we make two estimates of the required pumping efficiency below. In the first case we assume that the achievable divertor density will continue to be limited, and set this in combination with the allowable temperature to determine the divertor plasma conditions. In the second estimate, we instead set the divertor heat flux and temperature directly, which in turn determine the plasma density. The particle flux to the divertor surface is given by the well-known condition that flow is sonic at the entrance to the sheath
where
![]() $\Gamma _\parallel$
is the particle flux along the field lines and
$\Gamma _\parallel$
is the particle flux along the field lines and
![]() $c_s$
is the plasma sound speed. We have assumed that the electron and ion temperatures are the same in the divertor (
$c_s$
is the plasma sound speed. We have assumed that the electron and ion temperatures are the same in the divertor (
![]() $T_e=T_i=T$
). To date, the achievable divertor density in stellarators has been limited to of the order of
$T_e=T_i=T$
). To date, the achievable divertor density in stellarators has been limited to of the order of
![]() $n_{\text{div}} \approx 2n_{\text{sep}}$
(Jakubowski et al. Reference Jakubowski2021). As a first estimate, we impose this same constraint on the divertor density, and combine with the requirement that
$n_{\text{div}} \approx 2n_{\text{sep}}$
(Jakubowski et al. Reference Jakubowski2021). As a first estimate, we impose this same constraint on the divertor density, and combine with the requirement that
![]() $T_e \lesssim 10 eV$
to minimize physical erosion of the material surface (Stangeby Reference Stangeby2018); in this case, we allow the heat flux to be a free parameter. From these, the required pumping efficiency can be estimated as
$T_e \lesssim 10 eV$
to minimize physical erosion of the material surface (Stangeby Reference Stangeby2018); in this case, we allow the heat flux to be a free parameter. From these, the required pumping efficiency can be estimated as
where
![]() $\phi _{\text{pump}}$
and
$\phi _{\text{pump}}$
and
![]() $\phi _t$
are the required pumping and total particle flow to the divertor, respectively, in units of particles per second, and
$\phi _t$
are the required pumping and total particle flow to the divertor, respectively, in units of particles per second, and
![]() $A_{w}$
is the wetted area. Figure 2 shows the resulting required pumping efficiency as
$A_{w}$
is the wetted area. Figure 2 shows the resulting required pumping efficiency as
![]() $\lambda _{q,\perp }$
(and hence wetted area) is varied. Required efficiencies are shown for two values of the divertor temperature, 2 and 10 keV and an inclination angle
$\lambda _{q,\perp }$
(and hence wetted area) is varied. Required efficiencies are shown for two values of the divertor temperature, 2 and 10 keV and an inclination angle
![]() $\theta =3^\circ$
. As figure 2 shows, for low temperature
$\theta =3^\circ$
. As figure 2 shows, for low temperature
![]() $(T \sim 5 eV)$
and SOL widths of a few cm, pumping efficiencies in the range of a few percent, up to
$(T \sim 5 eV)$
and SOL widths of a few cm, pumping efficiencies in the range of a few percent, up to
![]() $\epsilon _p \approx 5\,\%$
, are required.
$\epsilon _p \approx 5\,\%$
, are required.

Figure 2. Required pumping efficiency
![]() $\epsilon _p$
as
$\epsilon _p$
as
![]() $\lambda _q$
is varied assuming
$\lambda _q$
is varied assuming
![]() $n_{\text{div}} \approx 2n_{\text{sep}}$
, for divertor temperature T = 2 (black) and 10 (blue) eV. Incidence angle
$n_{\text{div}} \approx 2n_{\text{sep}}$
, for divertor temperature T = 2 (black) and 10 (blue) eV. Incidence angle
![]() $\theta =3^\circ$
.
$\theta =3^\circ$
.
This serves as a conservative estimate, since it is expected that the larger islands characteristic of a full-sized FPP will improve access to the so-called high-recycling regime routinely observed on tokamaks (Krasheninnikov & Kukushkin Reference Krasheninnikov and Kukushkin2017). These larger islands will enable much higher divertor densities such that
![]() $n_{\text{div}} \gg n_{\text{sep}}$
is achievable (Pitts et al. Reference Pitts2019). Under these conditions, we can treat the divertor density as a free parameter and instead determine the particle flux based on the heat flux to the target and the plasma temperature. The target heat flux is related to the particle flux and the electron temperature via the sheath boundary condition
$n_{\text{div}} \gg n_{\text{sep}}$
is achievable (Pitts et al. Reference Pitts2019). Under these conditions, we can treat the divertor density as a free parameter and instead determine the particle flux based on the heat flux to the target and the plasma temperature. The target heat flux is related to the particle flux and the electron temperature via the sheath boundary condition
where
![]() $\gamma$
is the sheath heat transmission coefficient which takes on a value of
$\gamma$
is the sheath heat transmission coefficient which takes on a value of
![]() $\gamma \approx 7$
for the assumed conditions (
$\gamma \approx 7$
for the assumed conditions (
![]() $T_e\approx T_i$
) (Stangeby et al. Reference Stangeby2000) and
$T_e\approx T_i$
) (Stangeby et al. Reference Stangeby2000) and
![]() $Ry$
is the Rydberg energy. Integrating over the wetted area enables the total particle flow to the target to be related to the total power reaching the divertor,
$Ry$
is the Rydberg energy. Integrating over the wetted area enables the total particle flow to the target to be related to the total power reaching the divertor,
![]() $P_{\text{div}}$
,
$P_{\text{div}}$
,
where
![]() $P_{\text{tot}}$
is the sum of the alpha power and the auxiliary heating power. The radiated power fraction
$P_{\text{tot}}$
is the sum of the alpha power and the auxiliary heating power. The radiated power fraction
![]() $f_{\text{rad}}$
relates to the SOL width
$f_{\text{rad}}$
relates to the SOL width
![]() $\lambda _q$
through (3.4). As shown in figure 3, under such high-recycling conditions, significantly lower pumping efficiencies are required. With
$\lambda _q$
through (3.4). As shown in figure 3, under such high-recycling conditions, significantly lower pumping efficiencies are required. With
![]() $\epsilon _p \approx 0.5-1\,\,\%$
, adequate particle exhaust for low temperatures
$\epsilon _p \approx 0.5-1\,\,\%$
, adequate particle exhaust for low temperatures
![]() $(T \leq 5 eV)$
is possible. This can be viewed as an optimistic estimate. It assumes that the target heat flux, 5 MW/m
$(T \leq 5 eV)$
is possible. This can be viewed as an optimistic estimate. It assumes that the target heat flux, 5 MW/m
![]() $^2$
, hits the target. If the heat flux on the target is lower, then the required pumping efficiency is raised.
$^2$
, hits the target. If the heat flux on the target is lower, then the required pumping efficiency is raised.
These two estimates, taken together, serve to bracket the range of pumping efficiencies that will be required for Infinity Two. Accounting for the various uncertainties in the projected divertor parameters yields an overall range of
![]() $\epsilon _p \approx 0.5\,\%-5\,\%$
. Experimental measurements in W7-X have yielded values ranging from
$\epsilon _p \approx 0.5\,\%-5\,\%$
. Experimental measurements in W7-X have yielded values ranging from
![]() $\epsilon _p \approx 0.5\,\%$
to
$\epsilon _p \approx 0.5\,\%$
to
![]() $\epsilon _p \approx 2.9\,\%$
, with the lower end typical of the standard divertor configuration (Wenzel et al. Reference Wenzel2022). While these measurements cannot be directly compared with the pilot plant required efficiencies (doing so requires a detailed accounting of baffling, pumping and neutral transport that is not attempted here), they serve as an indication of what has been achieved to date.
$\epsilon _p \approx 2.9\,\%$
, with the lower end typical of the standard divertor configuration (Wenzel et al. Reference Wenzel2022). While these measurements cannot be directly compared with the pilot plant required efficiencies (doing so requires a detailed accounting of baffling, pumping and neutral transport that is not attempted here), they serve as an indication of what has been achieved to date.
The necessity of adequate exhaust, combined with the uncertainty around the heat-flux width scaling, influences the divertor design. If the heat-flux width is large, then a classical divertor with exhaust efficiency performance similar to W7-X will meet the requirements for Infinity Two. However, if heat-flux width is small, then new solutions are needed. In this paper we will present solutions for both scenarios. For large heat-flux width, we present the classical divertor solution in § 6. For small heat-flux width, below the values obtained from extrapolation of W7-X results, we present a new solution in § 7. This solution is the LIBD designed to improve pumping efficiency through closure of the divertor volume.

Figure 3. Value of
![]() $\epsilon _p$
vs
$\epsilon _p$
vs
![]() $\lambda _q$
based on total heat flux to the divertor without constraining the divertor density. Assumed divertor temperature T = 2 (black) and 10 (blue) eV, and incidence angle
$\lambda _q$
based on total heat flux to the divertor without constraining the divertor density. Assumed divertor temperature T = 2 (black) and 10 (blue) eV, and incidence angle
![]() $\theta =3^\circ$
.
$\theta =3^\circ$
.
5. Infinity Two island topology
The rotational transform profile in Infinity Two is tuned to have an
![]() $m$
= 5,
$m$
= 5,
![]() $n$
= 4 island chain at the edge (Hegna et al. Reference Hegna2025). Cross-sections of the plasma are shown in figure 4. The islands, shown in blue, magenta, and black, are fairly large with respect to the bulk plasma; this size was a design choice of necessity for proper performance of the LIBD, as discussed in § 7. The island separatrix is shown in orange. A representative vessel wall is also shown in green. This vessel wall serves as a simulation boundary for the edge calculations presented in this paper.
$n$
= 4 island chain at the edge (Hegna et al. Reference Hegna2025). Cross-sections of the plasma are shown in figure 4. The islands, shown in blue, magenta, and black, are fairly large with respect to the bulk plasma; this size was a design choice of necessity for proper performance of the LIBD, as discussed in § 7. The island separatrix is shown in orange. A representative vessel wall is also shown in green. This vessel wall serves as a simulation boundary for the edge calculations presented in this paper.

Figure 4. Poincaré plots of the configuration using the HINT equilibrium code. The island for the placement of the classical divertor is shown in blue. The island for the placement of the LIBD is shown in magenta. Orange is the island separatrix. The green represents a vessel wall which also serves as a simulation boundary in div3d and EMC3-Lite.
The islands have long connection lengths from about 1.6 km at the separatrix to close to 1 km 10 % in from the edge. Here, we measure the connection length as the length along a field line of a full circuit around the island. When structures are inserted, the connection lengths will change. It is expected that there will be transport perpendicular to the magnetic field lines in the islands. This transport will have the beneficial effect of spreading out the heat flux onto the target. The expected level of perpendicular transport can be extrapolated from W7-X, but there are significant unknowns. One of the most important and relevant unknown quantities is the scaling of the heat flux near the target,
![]() $\lambda _{q,\perp }$
with respect to magnetic field strength, the connection length and other parameters, as discussed in § 3.
$\lambda _{q,\perp }$
with respect to magnetic field strength, the connection length and other parameters, as discussed in § 3.
The island selected for the placement of the classical divertor is the top island in the
![]() $\phi$
= 0 plane, which is the top left island at the half-period. This island is highlighted in blue in figure 4.
$\phi$
= 0 plane, which is the top left island at the half-period. This island is highlighted in blue in figure 4.
A different location in the island chain is intercepted by the divertor dome for the LIBD divertor (§ 7). It is placed on the upper outboard island in the
![]() $\phi$
= 0 plane, which is also the top right island at the half-period. This island is highlighted in magenta in figure 4. The broad island shape is preferable for the LIBD divertor dome as it improves neutral confinement behind the divertor dome, where the pump ducts reside.
$\phi$
= 0 plane, which is also the top right island at the half-period. This island is highlighted in magenta in figure 4. The broad island shape is preferable for the LIBD divertor dome as it improves neutral confinement behind the divertor dome, where the pump ducts reside.
6. Heat-flux estimates on a classical island divertor
The LIBD (§ 7) shows promise as a concept that has excellent particle-exhaust efficiency and takes advantage of the robustness of detachment for power exhaust. However, it is a concept that has still not been validated experimentally. While we do plan to test this concept in Infinity One, it is prudent to also consider the classical, open, island divertor, which has been modeled extensively and tested experimentally, in particular in W7-X, as described in § 2.1. Hence, we also present estimates of heat fluxes for such a classical island divertor implemented in our power plant concept.
The location of the divertor plate for a classical island divertor is shown in figure 5. A representation of the three-dimensional divertor in the mirrored half-period is shown in figure 6. In figure 5, the divertor can be seen at three toroidal locations. The first at 5 degrees is near the beginning of the toroidal extent, where the divertor just intersects the edge of the island. The middle figure at 22.5 degrees is the location where the divertor has extended the furthest into the island structure surrounding the core plasma. The figure at 40 degrees shows the exit of the divertor plate from the island. The divertor creates a straight line in any constant
![]() $\phi$
plane, and thus makes a ruled surface in three dimensions. Two divertor plates will exist in each period, one being stellarator symmetric to the other, yielding 8 plates total for this configuration.
$\phi$
plane, and thus makes a ruled surface in three dimensions. Two divertor plates will exist in each period, one being stellarator symmetric to the other, yielding 8 plates total for this configuration.

Figure 5. Island divertor location at 3 toroidal planes: (a) 5 degrees, (b) 22.5 degrees, and (c) 40 degrees. Black dots represent Poincaré sections. The island separatrix is in orange. The blue solid line represents the divertor surface. The red dotted lines indicate the pumping gap. The green solid line is the vessel wall.

Figure 6. Three-dimensional model of the classical divertor with the Poincaré plot at
![]() $\phi$
= 22.5
$\phi$
= 22.5
![]() $^\circ$
in blue and the vessel wall in gray.
$^\circ$
in blue and the vessel wall in gray.
Shown in figure 7 are the connection lengths for the fusion power plant with the classic divertor inserted. As with W7-X, the island divertor cuts the island connection lengths by at least a factor of two, yielding a connection length of around 800 m near the separatrix and a bit lower inside the islands.

Figure 7. Connection lengths for the classical divertor calculated by EMC3-Lite.
An initial assessment of divertor performance was done with diffusive field-line following using the div3d code (Lore et al. Reference Lore2014). This concept can provide a first estimate for heat flux on primary divertor surfaces. The calculation is done by beginning field lines on a confined surface inside the plasma last closed flux surface. The field lines are then followed, and every half-degree they are given a perpendicular kick, to mimic perpendicular diffusion. We will refer to the perpendicular kick as the field-line diffusion coefficient. In this section a field-line diffusion coefficient of 1.0
![]() $\times$
10
$\times$
10
![]() $^{-6}$
m
$^{-6}$
m
![]() $^2$
/m was used.
$^2$
/m was used.
In this simple diffusion model the heat-flux width is solely a function of the geometry and the field-line diffusion coefficient. The scaling is given by
![]() $\lambda _{q,t} \propto \sqrt {L_c d}$
, where
$\lambda _{q,t} \propto \sqrt {L_c d}$
, where
![]() $d$
is the field-line diffusion coefficient and
$d$
is the field-line diffusion coefficient and
![]() $L_c$
is the connection length. Here, connection length plays the role of time in the typical diffusive model.
$L_c$
is the connection length. Here, connection length plays the role of time in the typical diffusive model.
Particles are followed until they intercept any of the surfaces. There are 3 possible interception surfaces: the main divertor surface (the blue lines in figure 5), the simulation boundary (green in figure 5) and not shown in figure 5 are the two toroidal endcaps that exist at the ends of the divertor and block particles from entering behind the divertor in the toroidal direction.
In the simulations presented in this paper, less than 0.05 % of particles are found to intersect the toroidal endcaps. The number of points intersecting the vessel wall is estimated at 2 %.
The results for the heat flux as calculated by div3d are shown in figure 8. In this plot the x-axis represents the distance along the divertor plate, while the y-axis is the toroidal angle in degrees.

Figure 8. Estimated heat flux on the divertor components for artificial diffusion of 1.0
![]() $\times$
10
$\times$
10
![]() $^{-6}$
m
$^{-6}$
m
![]() $^2$
m-1.
$^2$
m-1.
The heat flux is estimated by assuming a total power of 8 MW enters the plasma edge, corresponding to about a 95.6 % radiative fraction. Since the simulation is over a half-period, 1 MW enters each divertor section. The estimates of a maximum heat flux of 2.5 MW/m
![]() $^2$
is well below the design requirement of 10 MW/m
$^2$
is well below the design requirement of 10 MW/m
![]() $^2$
. Under these conditions, the requirement of the radiation fraction can be relaxed to 83.1 %; this would put the peak heat flux on the divertor at 9.5 MW/m
$^2$
. Under these conditions, the requirement of the radiation fraction can be relaxed to 83.1 %; this would put the peak heat flux on the divertor at 9.5 MW/m
![]() $^2$
. If the radiation flux is evenly distributed it will add an additional 0.15 MW/m
$^2$
. If the radiation flux is evenly distributed it will add an additional 0.15 MW/m
![]() $^2$
on the plasma-facing components (including those outside the divertor). The heat flux will remain under 10 MW/m
$^2$
on the plasma-facing components (including those outside the divertor). The heat flux will remain under 10 MW/m
![]() $^2$
provided the radiation peaking factor is under 3.2. In comparison, recent W7-X results show a peaking factor of 1.3 (Zhang et al. Reference Zhang2021).
$^2$
provided the radiation peaking factor is under 3.2. In comparison, recent W7-X results show a peaking factor of 1.3 (Zhang et al. Reference Zhang2021).
The heat flux profile on the divertor plates is well approximated by a Gaussian. The Gaussian-like behavior is due to employing the simplified field-line following model that does not attempt to resolve the complicated behavior inside the island. Furthermore, it does not account for drifts which have been shown to have an effect on the heat-flux behavior on W7-X (Hammond et al. Reference Hammond2019). An estimate of
![]() $\lambda _{q,t}$
is made by fitting the poloidal or cross-field heat-flux distribution at each toroidal slice with a Gaussian and then taking an average of the Gaussian width weighted by the height of the Gaussian. For the diffusion value used here, the
$\lambda _{q,t}$
is made by fitting the poloidal or cross-field heat-flux distribution at each toroidal slice with a Gaussian and then taking an average of the Gaussian width weighted by the height of the Gaussian. For the diffusion value used here, the
![]() $\lambda _{q,t}$
is calculated to be 2.9 cm. In this classical divertor design the angle that the island surfaces make with the divertor plate is approximately 90
$\lambda _{q,t}$
is calculated to be 2.9 cm. In this classical divertor design the angle that the island surfaces make with the divertor plate is approximately 90
![]() $^\circ$
(see figure 5). Therefore, we assume that
$^\circ$
(see figure 5). Therefore, we assume that
![]() $\lambda _{q_,\perp } \approx \lambda _{q,t}$
. Nevertheless, we will refer to the measured value
$\lambda _{q_,\perp } \approx \lambda _{q,t}$
. Nevertheless, we will refer to the measured value
![]() $\lambda _{q,t}$
in the rest of the section.
$\lambda _{q,t}$
in the rest of the section.
6.1. Behavior under variation of cross-field transport
The div3d calculation in the previous section was carried out at multiple diffusion values and the
![]() $\lambda _{q,t}$
values were measured at each case. The results are shown in figure 9. In addition to the estimate
$\lambda _{q,t}$
values were measured at each case. The results are shown in figure 9. In addition to the estimate
![]() $\lambda _{q,t}$
for 7 cases, we show a fit to a function
$\lambda _{q,t}$
for 7 cases, we show a fit to a function
![]() $\lambda _{q,t} \propto \sqrt {d}$
where
$\lambda _{q,t} \propto \sqrt {d}$
where
![]() $d$
is the field-line diffusion parameter in div3d. The fit shows deviation from the square root assumption at low values of
$d$
is the field-line diffusion parameter in div3d. The fit shows deviation from the square root assumption at low values of
![]() $d$
, indicating that geometric effects are likely complicating the simple analysis.
$d$
, indicating that geometric effects are likely complicating the simple analysis.

Figure 9. Plot of
![]() $\lambda _{q,t}$
from the weighted average of fits to div3d results. The red line is a fit of the
$\lambda _{q,t}$
from the weighted average of fits to div3d results. The red line is a fit of the
![]() $\lambda _{q,t}$
to the expected square root model.
$\lambda _{q,t}$
to the expected square root model.
Two additional calculations of the heat flux on the divertor are shown with
![]() $\lambda _{q,t}$
values of 8.7 cm (high diffusion) and 1.5 cm (low diffusion) in figure 10. At higher diffusion values, the heat flux is more spread out poloidally, and at lower heat fluxes it is more constrained to a small region around the location where the separatrix intersects the divertor structure. The peak heat flux at the higher diffusion values (figure 10
a) is very low, below 1 MW/m
$\lambda _{q,t}$
values of 8.7 cm (high diffusion) and 1.5 cm (low diffusion) in figure 10. At higher diffusion values, the heat flux is more spread out poloidally, and at lower heat fluxes it is more constrained to a small region around the location where the separatrix intersects the divertor structure. The peak heat flux at the higher diffusion values (figure 10
a) is very low, below 1 MW/m
![]() $^2$
. However, there is some concern with heat flux on other non-divertor components. Heat flux on the wall, for example, could be as high as 20 % of the total non-radiative heat flux. It should be noted that
$^2$
. However, there is some concern with heat flux on other non-divertor components. Heat flux on the wall, for example, could be as high as 20 % of the total non-radiative heat flux. It should be noted that
![]() $\lambda _{q,\perp }$
values of 8 cm are larger than are expected from W7-X scaling. However, if the cross-field transport does produce
$\lambda _{q,\perp }$
values of 8 cm are larger than are expected from W7-X scaling. However, if the cross-field transport does produce
![]() $\lambda _{q,t}$
values this high, the requirements on the radiation fraction can be reduced to under 58 %. However, there may need to be additional shielding applied to wall components in certain areas
$\lambda _{q,t}$
values this high, the requirements on the radiation fraction can be reduced to under 58 %. However, there may need to be additional shielding applied to wall components in certain areas

Figure 10. Estimated heat flux on the divertor components for (a)
![]() $\lambda _{q,t}$
= 8.7 cm and (b)
$\lambda _{q,t}$
= 8.7 cm and (b)
![]() $\lambda _{q,t}$
= 1.5 cm.
$\lambda _{q,t}$
= 1.5 cm.
At the low-diffusion values (figure 10
b) the heat flux exceeds 5 MW/m
![]() $^2$
in some places. The requirements on the radiation fraction can be reduced a little as well, but not below 90 % if the diffusion value is this low. It should be noted that there is some flexibility in the design of the classical divertor. Moving the divertor further away from the separatrix will increase connection length and allow for more spreading in the toroidal direction.
$^2$
in some places. The requirements on the radiation fraction can be reduced a little as well, but not below 90 % if the diffusion value is this low. It should be noted that there is some flexibility in the design of the classical divertor. Moving the divertor further away from the separatrix will increase connection length and allow for more spreading in the toroidal direction.
6.2. EMC3-lite calculations
In order to further clarify the heat flux on the target, the fluid edge code EMC3-Lite (Feng et al. Reference Feng2022) was used. The results from EMC3-Lite are presented in figure 11 for two diffusion values, a low value with the thermal diffusion coefficient
![]() $\chi =$
0.1 m
$\chi =$
0.1 m
![]() $^2$
s-1 and a high-diffusion case with
$^2$
s-1 and a high-diffusion case with
![]() $\chi =$
1.0 m
$\chi =$
1.0 m
![]() $^2$
s-1. The EMC3-Lite results show slightly different heat-flux behavior than that obtained from field-line diffusion. Namely, where field-line diffusion shows roughly even heat flux on both toroidal sides of the divertor plate, EMC3-Lite shows a strong preference for one side of the divertor plate. Nevertheless, the maximum heat-flux values are low enough to stay below the heat-flux limit of 10 MW/
$^2$
s-1. The EMC3-Lite results show slightly different heat-flux behavior than that obtained from field-line diffusion. Namely, where field-line diffusion shows roughly even heat flux on both toroidal sides of the divertor plate, EMC3-Lite shows a strong preference for one side of the divertor plate. Nevertheless, the maximum heat-flux values are low enough to stay below the heat-flux limit of 10 MW/
![]() $\text{m}^2$
.
$\text{m}^2$
.

Figure 11. Heat flux from EMC3-Lite for classical divertor with total power entering SOL is P
![]() $_{SOL}$
= 8 MW, electron temperature T
$_{SOL}$
= 8 MW, electron temperature T
![]() $_{e,sep}$
= 100 eV and electron density n
$_{e,sep}$
= 100 eV and electron density n
![]() $_{e,sep}$
= 1
$_{e,sep}$
= 1
![]() $\times$
10
$\times$
10
![]() $^{20}$
m
$^{20}$
m
![]() $^{-3}$
at separatrix. Thermal diffusion coefficient (a)
$^{-3}$
at separatrix. Thermal diffusion coefficient (a)
![]() $\chi$
= 0.1 m
$\chi$
= 0.1 m
![]() $^2$
s-1, (b)
$^2$
s-1, (b)
![]() $\chi$
= 1.0 m
$\chi$
= 1.0 m
![]() $^2$
s-1.
$^2$
s-1.
The low-diffusion heat-flux deposition profile looks most similar to the baseline case shown in figure 8. The high-diffusion case is similar to the high-diffusion plot in figure 10. The calculated peak heat flux in EMC3-Lite is roughly a factor of two over that calculated by div3d. This is because EMC3-Lite calculates that the heat flux will only deposit on one quadrant, rather than two quadrants as in div3d. For the high- and low-diffusion cases, the minimum required radiation fractions are 91 % and 81 %, respectively.
One additional feature visible in the high-diffusion EMC3-Lite calculations is the heat flux near the center of the divertor. This heat flux is located at the location where the divertor is maximally extended into the island. This heat flux could be caused by particles diffusing through the island entirely. This feature is less visible in the low-diffusion case.
To account for some of the discrepancies between EMC3-Lite and div3d we plot the connection length at the classical divertor in figure 12. Here, we see that the bottom right and top left quadrants have the longest connection lengths. The bottom left and top right quadrants have short connection lengths indicating that these divertor parts are shadowed by other divertor sections. The EMC3-Lite and div3d results show somewhat larger heat flux in the bottom left and top right shadowed quadrants, as expected from the modeling method. However, the lack of heat flux in the EMC3-Lite results in the top left quadrant cannot be explained from the connection length plot.

Figure 12. Connection lengths over the surface of the classical divertor, calculated by div3d.
The discrepancy between EMC3-Lite and div3d indicates the need to simulate the edge with a full edge code, such as EMC3-EIRENE, as well as the need to gather more experimental data on the behavior of island divertor operations.
6.3. Vacuum field behavior
To examine the performance at startup, we repeat the calculation with the divertor plate in the vacuum magnetic field and the results are shown in figure 13(b). The difference between the vacuum fields and the HINT fields at full plasma pressure are shown in figure 13(a). In the vacuum field, the divertor plates are no longer well-aligned with the magnetic island. However, because the device is quasi-isodynamic, the evolution of the field is minimal and the heat-flux distribution remains acceptable.

Figure 13. (a) Close view of Poincaré plot at
![]() $\phi$
= 22.5
$\phi$
= 22.5
![]() $^\circ$
with the vacuum fields (red) superimposed. (b) Heat flux on the divertor plate assuming 8 MW of outflowing power and the vacuum fields generated from the coils without plasma effects.
$^\circ$
with the vacuum fields (red) superimposed. (b) Heat flux on the divertor plate assuming 8 MW of outflowing power and the vacuum fields generated from the coils without plasma effects.
7. Large island backside divertor
The classical island divertor presented in § 6 can handle the heat-flux requirements for the power plant, however, the containment of the neutrals is poor in W7-X, very likely due to the openness of the divertor. In this section, we present a novel concept: the LIBD that can be used to confine the neutrals by essentially being closed. The divertor concept works by exploiting the fact that the majority of the heat flux streaming out of the core plasma travels along the separatrix around the islands. Therefore, the interior of the islands is sheltered from the direct outflow of plasma and is a suitable location for an internal structure that prevents the neutral particles from directly reentering the plasma.
A representation of the concept is given in figure 14. The Poincaré plot, in blue, shows large magnetic islands around the edge. The dome structure (yellow) is inserted into the island interior. The plasma flows around the dome and hits an impact surface (blue). The LIBD design also includes baffles, not shown. The narrow gap between the dome and baffles prevents neutrals from reentering the plasma, forcing them into the pumping gaps where they can be exhausted.

Figure 14. Three-dimensional view of the LIBD for the fusion power plant configuration. A Poincare plot at the
![]() $\phi$
= 22.5
$\phi$
= 22.5
![]() $^\circ$
surface is shown in blue. The LIBD dome is yellow, the impact surfaces are blue and the support is pink. The design also includes baffles, not shown in this image.
$^\circ$
surface is shown in blue. The LIBD dome is yellow, the impact surfaces are blue and the support is pink. The design also includes baffles, not shown in this image.
In each half-field period the LIBD extends approximately 7.95 m toroidally. The shape of the LIBD changes so that the dome center roughly follows the contours of the island, and then tapers somewhat towards the toroidal ends. The impact surfaces are positioned such that the angle of impact with the magnetic field is about 3 degrees at all points.
The dome is connected to the wall with a support structure (pink in figure 14). Because of the dome’s placement in the island interior, the island separatrix passes behind the dome and intersects the support. At this point of intersection, near the attachment point of support to dome, the support surfaces are angled to help direct neutral particles into the pumping duct. These angled surfaces are the “impact surfaces” (blue in figure 14) and are the desired location for the heat flux. In addition to these structures, two outer baffles are located on either side of the LIBD to help constrain neutral particles further, and together with the outflowing plasma, prevent neutrals from streaming out of the subdivertor volume since they will be reionized by the outflowing plasma, entrained in its flow by collisions and redeposited in the support region. This will allow maintaining a high neutral pressure in the subdivertor region and a comparably low neutral pressure in the main plasma chamber. The baffle extends in the poloidal direction until close to the island x-point so that the channel between the baffles and the dome is as long as possible. These baffles are a distinguishing feature from similar concepts previously attempted such as the local island divertor in LHD (Morisaki et al. Reference Morisaki, Masuzaki, Suzuki, Komori, Ohyabu, Motojima, Okamura and Matsuoka2003, Reference Morisaki2005).

Figure 15. Connection lengths at the
![]() $\phi = 22.5^\circ$
plane. The LIBD divertor components are colored with the dome in orange, the baffles in green, the support in pink and the impact surfaces in blue.
$\phi = 22.5^\circ$
plane. The LIBD divertor components are colored with the dome in orange, the baffles in green, the support in pink and the impact surfaces in blue.
Figure 15 shows the connection lengths in the edge at the quarter period,
![]() $\phi = 22.5^\circ$
, along with the two-dimensional cross-section of the LIBD. Here, we show the dome, impact surfaces and supports as in figure 14, as well as the vacuum vessel (gray) and baffles (green). The structure of the
$\phi = 22.5^\circ$
, along with the two-dimensional cross-section of the LIBD. Here, we show the dome, impact surfaces and supports as in figure 14, as well as the vacuum vessel (gray) and baffles (green). The structure of the
![]() $L_c$
is also shown at a different island in the top left of figure 15. Here, the field lines that intersect the dome directly appear in purple. Due to the
$L_c$
is also shown at a different island in the top left of figure 15. Here, the field lines that intersect the dome directly appear in purple. Due to the
![]() $\rm m$
= 5 periodicity of the islands, these field lines will intersect the dome both by traveling one field period in one direction and four field periods in the reverse direction. Around the purple region it is possible to see striations in the connection length depending on how many traversals are needed before a field line intersects the support or the impact surfaces.
$\rm m$
= 5 periodicity of the islands, these field lines will intersect the dome both by traveling one field period in one direction and four field periods in the reverse direction. Around the purple region it is possible to see striations in the connection length depending on how many traversals are needed before a field line intersects the support or the impact surfaces.
The physical presence of the LIBD dome inside the island necessitates islands of sufficient radial width, given that the dome will need to be structurally sound and actively cooled. Large islands are most easily created in low-shear stellarators, and the combination of large island size and low shear implies a long connection length. This means perpendicular transport can be very effective in widening the SOL. A circumstance that is challenging to the LIBD occurs when perpendicular transport is sufficiently large that the island width is comparable to the SOL width. Perpendicular transport will cause particles to transit across the island faster than parallel transport will move them around the island to the backside of the dome, and the particles will intersect the dome on its front as much as – if not more than – the backside. This scenario can be avoided with sufficiently large islands or improved understanding of cross-field transport processes in the island region.
7.1. Heat-flux handling of the LIBD

Figure 16. Relationship between the heat-flux width and the field-line diffusion coefficient in div3d for the LIBD. The two impact surfaces are on opposite sides of the dome.
As with the classical divertor we can calculate the relationship between the heat flux on the impact surfaces and the diffusion parameter that we input into the div3d code. The relationship is shown in figure 16 and is calculated by only considering the impact surfaces. While the classical divertor showed a clear square root relationship between the heat flux and the numerical diffusion coefficient, the story in the LIBD is more complicated. The two impact surfaces on either side of the LIBD show slightly different scalings, and the power-scaling parameters both deviate from the square root scaling. For one surface the exponent in the power law is 0.33 and in the other it is 0.40.
Using the scaling from support 1, we analyze the functionality of the full LIBD as a function of the diffusion parameter. The results are shown in figure 17. The desired location of the strike lines is the impact surface shown in orange. As can be seen, below about
![]() $\lambda _{q,t}$
= 1 cm the majority of the heat flux hits the impact surfaces. At larger values of
$\lambda _{q,t}$
= 1 cm the majority of the heat flux hits the impact surfaces. At larger values of
![]() $\lambda _{q,t}$
significant heat flux appears on the dome and on the baffles. While these structures will need to be designed to handle some heat flux, the good neutral confinement properties of the LIBD will only be possible if most of the heat flux hits either the impact surfaces or the back side of the dome.
$\lambda _{q,t}$
significant heat flux appears on the dome and on the baffles. While these structures will need to be designed to handle some heat flux, the good neutral confinement properties of the LIBD will only be possible if most of the heat flux hits either the impact surfaces or the back side of the dome.
We relate the simulated
![]() $\lambda _{q,t}$
to
$\lambda _{q,t}$
to
![]() $\lambda _{q,\perp }$
by taking into account the tilt of the impact surface with respect to the island flux surfaces. This characteristic angle is 33
$\lambda _{q,\perp }$
by taking into account the tilt of the impact surface with respect to the island flux surfaces. This characteristic angle is 33
![]() $^\circ$
yielding a value of
$^\circ$
yielding a value of
![]() $\lambda _{q,\perp }$
for the LIBD of 0.8 cm.
$\lambda _{q,\perp }$
for the LIBD of 0.8 cm.

Figure 17. Estimation of the fraction of heat-flux load on components as a function of the characteristic heat-flux length,
![]() $\lambda _{q,t}$
(m). All components are shown with their strikes as a fraction of the total lines that hit components or wall in one half-field period.
$\lambda _{q,t}$
(m). All components are shown with their strikes as a fraction of the total lines that hit components or wall in one half-field period.
There is some flexibility in the design of the LIBD depending on improved knowledge regarding edge diffusion parameters and heat-flux scaling. If the edge diffusion values are low,
![]() $\lambda _{q,\perp }$
is small, and then the dome can be enlarged and the gap between baffles and the island separatrix can be reduced. Alternatively, the islands themselves can be reduced in size. In either case, heat-flux exhaust will be more difficult and a higher radiative fraction will be needed. On the other hand, if the edge diffusion values are larger,
$\lambda _{q,\perp }$
is small, and then the dome can be enlarged and the gap between baffles and the island separatrix can be reduced. Alternatively, the islands themselves can be reduced in size. In either case, heat-flux exhaust will be more difficult and a higher radiative fraction will be needed. On the other hand, if the edge diffusion values are larger,
![]() $\lambda _{q,\perp }$
increases, and the dome must be made smaller so the gap between the dome and the baffles is large enough to accommodate the heat-flux channel. Since this region will be filled with a wider SOL outflow, it should still be preventing neutral particles from leaving through that gap. However, this may require even more of the plasma volume to be devoted to the islands.
$\lambda _{q,\perp }$
increases, and the dome must be made smaller so the gap between the dome and the baffles is large enough to accommodate the heat-flux channel. Since this region will be filled with a wider SOL outflow, it should still be preventing neutral particles from leaving through that gap. However, this may require even more of the plasma volume to be devoted to the islands.
The heat flux as a function of toroidal angle for the divertor components is shown in figure 18. The values are shown for two values of
![]() $d$
. The left plot has the results for
$d$
. The left plot has the results for
![]() $\lambda _{q,t} \approx$
0.5 cm where almost all the heat flux is located on the impact surfaces. The right plot shows the results for
$\lambda _{q,t} \approx$
0.5 cm where almost all the heat flux is located on the impact surfaces. The right plot shows the results for
![]() $\lambda _{q,t} \approx$
1.1 cm where there is some heat flux on the dome and baffles.
$\lambda _{q,t} \approx$
1.1 cm where there is some heat flux on the dome and baffles.

Figure 18. Heat flux per toroidal angle for each set of components when
![]() $\lambda _{q,t} \approx$
0.5 cm (low diffusion, left) and for
$\lambda _{q,t} \approx$
0.5 cm (low diffusion, left) and for
![]() $\lambda _{q,t} \approx$
1.1 cm (high diffusion, right).
$\lambda _{q,t} \approx$
1.1 cm (high diffusion, right).
As with the classical divertor, we estimate the heat flux by assuming 8 MW of power are exhausted by the divertor. The results for the two impact surfaces (one on each side) is given in figure 19. The heat flux is predominately located on one toroidal side of the impact surfaces, with a strong concentration near the end at 0.1 radians. For the low-diffusion LIBD, the required radiation fraction is around 94 %. However, the calculation of the radiation component on the impact surfaces of the LIBD depends strongly on the position of the radiation front. Further adjustments of the LIBD can be made as more updated information arrives regarding the edge transport behavior.

Figure 19. Heat flux on the two impact surfaces for
![]() $d$
= 1.0
$d$
= 1.0
![]() $\times$
10
$\times$
10
![]() $^{-7}$
m
$^{-7}$
m
![]() $^2$
m-1.
$^2$
m-1.
While very high levels of radiative power is obviously beneficial to the long-term survival of the Plasma facing components (PFCs), it should be noted that very deep detachment, in particular the extreme version that leads to plasma shrinkage, is likely detrimental to the efficiency of the LIBD’s particle-exhaust efficiency. If the plasma temperature in the SOL drops too far, the plasma particles may not be able to reach the backside of the dome before they have diffused across the magnetic field to its front side, in which case the dome would start acting as a limiter rather than a divertor. A program is planned for the optimization of the dome and island shapes, as well as the edge-plasma radiation intensity to address this. Experimental validation of the concept will be performed in the Infinity One stellarator.
7.2. Particle exhaust of the LIBD
In this section we present a simple two-dimensional model to estimate the particle exhaust in the LIBD. A model of the LIBD is created in slab geometry and is shown in figure 20. The horizontal axis represents a poloidal-like direction and the vertical axis represents the radial-like direction. The toroidal-like direction is in and out of the plane. The divertor extends for a finite length in the toroidal-like direction of 7.95 m, corresponding to the toroidal extent of the actual LIBD shown above. Plasma arrives from the divertor entrance (pink arrows) and impacts on the slanted impact surface. Neutral hydrogen atoms are created near the impact surface and are given an initial velocity corresponding to 4 eV Franck–Condon energy from molecular dissociation (yellow arrows). The initial distribution is uniform in the toroidal-like direction. In the radial-like direction, particles are sourced with a normal distribution, which will be described in more detail below.

Figure 20. Geometry of the simple neutral slab model for the LIBD. All unlabeled units are in millimeters. The orange component is the dome, the pink is the support, the blue is the impact surface and the green is the baffle.
Particles are followed along ballistic trajectories until one of the following occurs:
-
The particle escapes either through the slit opening in the poloidal-like direction, the ends in the toroidal-like direction, or is pumped through the pumping duct. In all these cases, the particle is logged and is no longer followed.
-
The particle hits a surface, in which case it is reflected assuming perfect mirror reflection.
-
The particle ionizes in the divertor volume.
We note that more advanced models should assume a better reflection model, and a poloidal-like dependence of the plasma parameters.
The initial position in the radial-like direction follows a normal distribution centered around the island separatrix. For this calculation the characteristic widths for temperature and density,
![]() $\lambda _T$
is 0.1 m and
$\lambda _T$
is 0.1 m and
![]() $\lambda _n$
is 0.01 m. The peak density is given as 2
$\lambda _n$
is 0.01 m. The peak density is given as 2
![]() $\times$
10
$\times$
10
![]() $^{20}$
m
$^{20}$
m
![]() $^{-3}$
, and the peak temperature is given as 10 eV. In both cases, the profiles remain constant along the poloidal-like direction.
$^{-3}$
, and the peak temperature is given as 10 eV. In both cases, the profiles remain constant along the poloidal-like direction.
The chance of electron-impact ionization at any point in time is given by
where
![]() $T$
is the temperature in eV,
$T$
is the temperature in eV,
![]() $n$
is the density in m
$n$
is the density in m
![]() $^{-3}$
and
$^{-3}$
and
![]() $t$
is the time step in seconds (Maingi et al. Reference Maingi, Watkins, Mahdavi and Owen1999). We do not consider any other forms of ionization, or charge exchange in this simplistic model.
$t$
is the time step in seconds (Maingi et al. Reference Maingi, Watkins, Mahdavi and Owen1999). We do not consider any other forms of ionization, or charge exchange in this simplistic model.
In the simulation, 87.0
![]() $\pm$
0.1 % of particles ionized in the divertor volume. Of the particles that escape, 12.6
$\pm$
0.1 % of particles ionized in the divertor volume. Of the particles that escape, 12.6
![]() $\pm$
0.1 % are pumped and 0.46
$\pm$
0.1 % are pumped and 0.46
![]() $\pm$
0.03 % of particles escape the divertor structure back into the plasma. Over 95 % of the neutral particles that leave the divertor region escape in the toroidal-like direction. An estimated exhaust efficiency of 12.6 % compares favorably with the requirements under all scenarios described in § 4, although more detailed analysis is necessary to refine this estimate and determine the requirements of the pumping system.
$\pm$
0.03 % of particles escape the divertor structure back into the plasma. Over 95 % of the neutral particles that leave the divertor region escape in the toroidal-like direction. An estimated exhaust efficiency of 12.6 % compares favorably with the requirements under all scenarios described in § 4, although more detailed analysis is necessary to refine this estimate and determine the requirements of the pumping system.
8. Discussion and conclusion
The heat-flux exhaust, a concern for a FPP, is solvable in stellarators for several reasons. The primary reason is the stable and reproducible access to deep divertor detachment. The secondary reason relates to attached operation in divertor solutions employing a sizable edge island chain. Due to the uncertainties in the dependence on the target heat-flux width,
![]() $\lambda _{q,t}$
, on connection length and field strength, there is range of plausible values of
$\lambda _{q,t}$
, on connection length and field strength, there is range of plausible values of
![]() $\lambda _{q,t}$
in Infinity Two. We analyzed a design of a classical island divertor for our stellarator power plant concept, and found that it has acceptable levels of heat flux. The classical island divertor possesses flexibility in that it can be placed deeper in or further out, thereby adjusting the connection length and providing an appropriate heat-flux profile. This alone does not automatically guarantee long-term survival of the divertor for attached conditions, since physical sputtering may lead to excessive erosion. However, deep detachment is associated with much reduced plasma temperatures at the divertor targets, and should feasibly allow for benign erosion of power-plant-relevant plasma-facing component materials such as tungsten.
$\lambda _{q,t}$
in Infinity Two. We analyzed a design of a classical island divertor for our stellarator power plant concept, and found that it has acceptable levels of heat flux. The classical island divertor possesses flexibility in that it can be placed deeper in or further out, thereby adjusting the connection length and providing an appropriate heat-flux profile. This alone does not automatically guarantee long-term survival of the divertor for attached conditions, since physical sputtering may lead to excessive erosion. However, deep detachment is associated with much reduced plasma temperatures at the divertor targets, and should feasibly allow for benign erosion of power-plant-relevant plasma-facing component materials such as tungsten.
Experiments on the island divertor at W7-X have indicated a weakness of the classic island divertor concept, namely that neutral pumping efficiency is poor. This is primarily due to the divertor being an open divertor and one that is designed to accommodate several distinct magnetic configurations. While restricting to a single configuration could make an open divertor better baffled, an open divertor geometry will always have the material surfaces where the neutrals are being created from the SOL outflow face the core plasma region instead of the subdivertor region and the pumps. Optimization of baffling design to improve neutral confinement is one solution, and will be a subject of future efforts. We also present a different remedy to this issue, an alternate design, the LIBD. This divertor closes off pathways for neutralized plasma particles to escape back into the plasma and forces them into the divertor pumping gap in a way reminiscent of closed tokamak divertor concepts, which have been shown to have good particle-exhaust efficiency. A simplified first assessment of the particle-exhaust efficiency of such a divertor confirms this. More detailed assessments are currently not available, due to existing codes not yet being compatible with the LIBD concept.
The functioning of the LIBD and the positioning of the classic divertor both depend on having proper estimations of
![]() $\lambda _{q,\perp }$
, whose parametric dependencies are not yet understood very well in stellarators. This points to the need for further experiments, either in W7-X or in a new dedicated stellarator device with very long connection lengths. It is especially advantageous if data can be obtained for very long connection lengths and for magnetic field strengths different from the magnetic field strengths so far used in operation in W7-X, which are within 10 % of 2.5 T. These should allow for a more robust empirical scaling law and potentially a better theoretical insight into the fundamental scalings.
$\lambda _{q,\perp }$
, whose parametric dependencies are not yet understood very well in stellarators. This points to the need for further experiments, either in W7-X or in a new dedicated stellarator device with very long connection lengths. It is especially advantageous if data can be obtained for very long connection lengths and for magnetic field strengths different from the magnetic field strengths so far used in operation in W7-X, which are within 10 % of 2.5 T. These should allow for a more robust empirical scaling law and potentially a better theoretical insight into the fundamental scalings.
The work here represents an initial exploration of the performance of a classical divertor and an LIBD. The sensitivity to field errors, or what external control coils, if any, are necessary to reach the operating regime is left to future work. Various experimental and numerical studies on W7-X and other stellarators have shown that overloading of plasma-facing components due to sensitivity of plasma edge structure to a change in plasma pressure or during the evolution of the toroidal current density toward its steady-state profile could be controlled by transient modification of the magnetic configuration by external current drive (Geiger et al. Reference Geiger, Beidler, Drevlak, Maaßberg, Nührenberg, Suzuki and Turkin2010; Zanini et al. Reference Zanini2020) or by changing the currents in the field coils (Murakami et al. Reference Murakami1991; López-Bruna et al. Reference López-Bruna2009). These techniques are planned to be tested in Infinity One.
The Type One Energy FusionDirect plan calls for an intermediate scale device, Infinity One. Among its research goals is a plan to clarify the edge transport behavior in stellarators and test the constructability and viability of improved divertor designs such as the LIBD.
Acknowledgements
Type One Energy Group would like to acknowledge Dr Y. Feng and Dr Y. Gao for assistance in compiling and running the EMC3-Lite code, as well as Dr J. Lore for assistance in compiling and running the div3d code.
Editor Per Helander thanks the referees for their advice in evaluating this article.
Declaration of interests
The authors report no conflict of interest.