The evolution of vertical and horizontal thermals is examined via three-dimensional numerical simulations. The two types of thermals are distinguished by the geometry of their sources: respectively spherical and horizontal cylindrical. How the evolution of a vertical thermal is affected by varying the Reynolds number from the laminar regime into the fully turbulent regime is examined. Although the rate of rise of a thermal increases with increasing Reynolds number in the laminar regime, it is shown here that it decreases with increasing Reynolds number in the turbulent regime. Known instabilities of vortex rings and vortex dipoles are shown to affect the evolution of the vertical and horizontal thermals, respectively. In particular, the short-wave cooperative instability, commonly seen in the evolution of contrails behind aircraft, is a major influence on the evolution of the horizontal thermal. The vortex dynamics during the encounter of both types of thermals with a strong thermocline is examined. It is found that, when blocked by a thermocline, the head of the vertical thermal is dispersed laterally by the action of small compact vortex dipoles that are produced during the collision. Evidence is presented for the propagation of circular waves in the thermocline that spread out horizontally moving away from the impact site. In the case of the horizontal thermal, the collision with the thermocline results in vortex dynamics similar to that which occurs when a dipole impinges on a no-slip wall.

Many permeable aquifers have vertical variations in the permeability, which are correlated over long lateral distances. When a buoyant high viscosity fluid is injected into a permeable aquifer and displaces a less viscous fluid, the interface that develops has finite extent and travels with constant speed. The effect of the permeability variations leads to fluid in the high permeability regions travelling into the front, where it migrates into the lower permeability part. Subsequently, it lags progressively further behind the advancing front. We explore the influence of this cycling on the dispersion of a tracer or additive in the fluid to determine its distribution within the current as a function of time. At early times tracer is sheared owing to the vertically varying permeability. At later times, cross-aquifer diffusion homogenises the tracer distribution, which spreads longitudinally at a faster rate than by diffusion alone in this shear dispersion regime. Eventually, tracer reaches the front of the current. This acts as a no-flux boundary and the concentration profile transitions to a half-Gaussian, with the maximum concentration at the front. The centre of mass of the tracer spreads backwards relative to the fixed nose at a rate proportional to $(DT)^{1/2}$, where T is time and D is the diffusion coefficient. The initial release of tracer may not be vertically uniform owing to the heterogeneity and we show that this can lead to the centre of mass of tracer initially advancing faster than the mean flow. Although our model is highly idealised, it illustrates how, owing to a vertical variation of permeability, it is possible for a finite pulse of tracer or chemical added after the start of injection to reach the front with important implications for tracer tests and strategies for enhanced recovery.

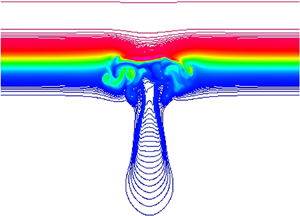
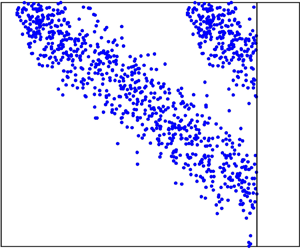
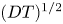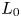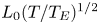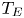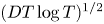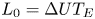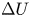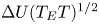We consider the injection of a buoyant low viscosity fluid into an aquifer saturated with a higher viscosity fluid. The nose region of the flow, where the thickness of the injected fluid is less than the thickness of the aquifer, grows in proportion to time and as a result fluid continually migrates further into the nose where it has a progressively smaller vertical extent. We explore how the flow in the nose influences the migration of a pulse of tracer. 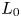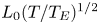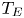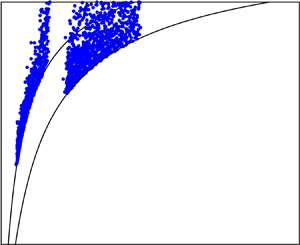The growth of the nose stretches a pulse of tracer of initial length, $L_0$, longitudinally to have a length proportional to $L_0 (T/T_E)^{1/2}$, where $T_E$ is the nose entry time. Diffusion acts at the same rate and the combination of the two processes results in an tracer spreading longitudinally with a length proportional to 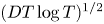$(D T\, \log T)^{1/2}$ at long times after entering the nose, where D is the coefficient of diffusion. The results are generalised to consider the case in which the permeability in the aquifer varies with depth. At early times, the tracer is sheared. As the tracer migrates into continually thinner regions of the growing nose, the permeability contrast sampled by the tracer rapidly decays. The role of the shear becomes dominated by the stretching of the nose and ultimately the late-time behaviour is as in a uniform aquifer. However, the effective pulse length of the tracer upon asymptoting to the stretching regime is now given by 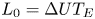$L_0={\rm \Delta} U T_E$, where 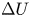${\rm \Delta} U$ is the magnitude of the shear. The spreading in the stretching regime then has a length scale of 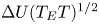${\rm \Delta} U (T_E T)^{1/2}$, which may be much faster than in the case of a uniform aquifer. If the diffusion is sufficiently fast, there may be an intermediate regime in which Taylor dispersion is important prior to the stretching dominating.