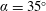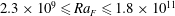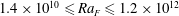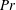Papers
Compressible starting jet: pinch-off and vortex ring–trailing jet interaction
-
- Published online by Cambridge University Press:
- 27 March 2017, pp. 560-589
-
- Article
- Export citation
Vortex-induced vibration and galloping of prisms with triangular cross-sections
-
- Published online by Cambridge University Press:
- 24 March 2017, pp. 590-618
-
- Article
- Export citation
JFM Perspectives
The engine behind (wall) turbulence: perspectives on scale interactions
-
- Published online by Cambridge University Press:
- 24 March 2017, P1
-
- Article
- Export citation
Rapids
Thermal convection with mixed thermal boundary conditions: effects of insulating lids at the top
-
- Published online by Cambridge University Press:
- 15 March 2017, R1
-
- Article
- Export citation
Simulation and feedback control of the Ahmed body flow exhibiting symmetry breaking behaviour
-
- Published online by Cambridge University Press:
- 15 March 2017, R2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sustaining processes from recurrent flows in body-forced turbulence
-
- Published online by Cambridge University Press:
- 24 March 2017, R3
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
FLM volume 817 Cover and Front matter
-
- Published online by Cambridge University Press:
- 07 April 2017, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
FLM volume 817 Cover and Back matter
-
- Published online by Cambridge University Press:
- 07 April 2017, pp. b1-b6
-
- Article
-
- You have access
- Export citation