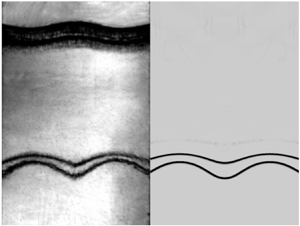
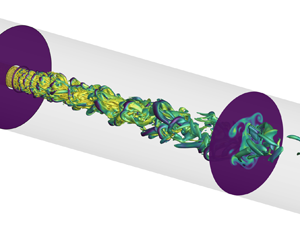
Graphical abstract from Constante-Amores, C., Abadie, T., Kahouadji, L., Shin, S., Chergui, J., Juric, D., Castrejón-Pita, A.A. & Matar, O. 2023 Direct numerical simulations of turbulent jets: vortex-interface-surfactant interactions. J. Fluid Mech. 955, A42. doi:10.1017/jfm.2022.1056.
JFM Papers
Particle-size segregation in self-channelized granular flows
-
- Published online by Cambridge University Press:
- 20 January 2023, A38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Identification of the energy contributions associated with wall-attached eddies and very-large-scale motions in the near-neutral atmospheric surface layer through wind LiDAR measurements
-
- Published online by Cambridge University Press:
- 23 January 2023, A39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hydrodynamic instabilities of two successive slow/fast interfaces induced by a weak shock
-
- Published online by Cambridge University Press:
- 23 January 2023, A40
-
- Article
- Export citation
Thermodynamically consistent phase-field modelling of activated solute transport in binary solvent fluids
-
- Published online by Cambridge University Press:
- 24 January 2023, A41
-
- Article
- Export citation
Direct numerical simulations of turbulent jets: vortex–interface–surfactant interactions
-
- Published online by Cambridge University Press:
- 24 January 2023, A42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Coaxial jets with disparate viscosity: mixing and laminarization characteristics
-
- Published online by Cambridge University Press:
- 25 January 2023, A43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Corrigendum
Comparison of the compressible μ(I) class of models and non-local models with the discrete element method (DEM) for steady fully developed flow of cohesionless granular materials through a vertical channel – CORRIGENDUM
-
- Published online by Cambridge University Press:
- 24 January 2023, E1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Front Cover (OFC, IFC) and matter
FLM volume 955 Cover and Front matter
-
- Published online by Cambridge University Press:
- 30 January 2023, pp. f1-f2
-
- Article
-
- You have access
- Export citation