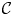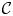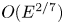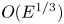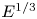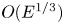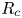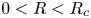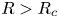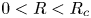We investigate the linear properties of the steady and axisymmetric stress-driven spin-down flow of a viscous fluid inside a spherical shell, both within the incompressible and anelastic approximations, and in the asymptotic limit of small viscosities. From boundary layer analysis, we derive an analytical geostrophic solution for the three-dimensional incompressible steady flow, inside and outside the cylinder $\mathcal {C}$ that is tangent to the inner shell. The Stewartson layer that lies on $\mathcal {C}$ is composed of two nested shear layers of thickness $O(E^{2/7})$ and $O(E^{1/3})$ where E is the Ekman number. We derive the lowest-order solution for the $E^{2/7}$-layer. A simple analysis of the $E^{1/3}$-layer lying along the tangent cylinder, reveals it to be the site of an upwelling flow of amplitude $O(E^{1/3})$. Despite its narrowness, this shear layer concentrates most of the global meridional kinetic energy of the spin-down flow. Furthermore, a stable stratification does not perturb the spin-down flow provided the Prandtl number is small enough. If this is not the case, the Stewartson layer disappears and meridional circulation is confined within the thermal layers. The scalings for the amplitude of the anelastic secondary flow have been found to be the same as for the incompressible flow in all three regions, at the lowest order. However, because the velocity no longer conforms the Taylor–Proudman theorem, its shape differs outside the tangent cylinder $\mathcal {C}$, that is, where differential rotation takes place. Finally, we find the settling of the steady state to be reached on a viscous time for the weakly, strongly and thermally unstratified incompressible flows. Large density variations relevant to astro- and geophysical systems, tend to slightly shorten the transient.

In the present study, compressible low-Reynolds-number flow past a stationary isolated sphere was investigated by direct numerical simulations of the Navier–Stokes equations using a body-fitted grid with high-order schemes. The Reynolds number based on free-stream quantities and the diameter of the sphere was set to be between 250 and 1000, and the free-stream Mach number was set to be between 0.3 and 2.0. As a result, it was clarified that the wake of the sphere is significantly stabilized as the Mach number increases, particularly at the Mach number greater than or equal to 0.95, but turbulent kinetic energy at the higher Mach numbers conditions is higher than that at the lower Mach numbers conditions of similar flow regimes. A rapid extension of the length of the recirculation region was observed under the transitional condition between the steady and unsteady flows. The drag coefficient increases as the Mach number increases mainly in the transonic regime and its increment is almost due to the increment in the pressure component. In addition, the increment in the drag coefficient is approximately a function of the Mach number and independent of the Reynolds number in the continuum regime. Moreover, the effect of the Mach and Reynolds numbers on the flow properties such as the drag coefficient and flow regime can approximately be characterized by the position of the separation point.

Kinetic energy and enstrophy transfer in compressible Rayleigh–Taylor (RT) turbulence were investigated by means of direct numerical simulation. It is revealed that compressibility plays an important role in the kinetic energy and enstrophy transfer based on analyses of transport and large-scale equations. For the generation and transfer of kinetic energy, some findings have been obtained as follows. The pressure-dilatation work dominates the generation of kinetic energy in the early stage of flow evolution. The baropycnal work and deformation work handle the kinetic energy transfer from large to small scales on average for RT turbulence. The baropycnal work is mainly responsible for the kinetic energy transfer on large scales, and the deformation work for the kinetic energy transfer on small scales. The baropycnal work is also disclosed to be related to the compressibility from the finding that the expansion motion enhances the positive baropycnal work and the compression motion strengthens the negative baropycnal work. For the generation and transfer of enstrophy, the horizontal enstrophy is generated by the baroclinic effect and the vertical enstrophy by vortex stretching and tilting. Then the enstrophy is strengthened by the vortex stretching and tilting during the evolution of RT turbulence and the vorticity tends to be isotropic in the turbulent mixing region. The large-scale enstrophy equation in compressible flow has also been derived to deal with the enstrophy transfer. It is identified that the enstrophy is transferred from large to small scales on average and tends to stabilize for RT turbulence.

The long-lasting response of turbulent pipe flow to a step change in surface roughness from rough to smooth is examined. Global flow characteristics such as the pressure gradient, skin friction and mean streamwise momentum attain their equilibrium values within approximately 20 radii downstream of the step change, but the turbulent stresses are exceedingly slow to adjust to the new wall condition (${>}120\ \textrm {radii}$), and they first fall below their equilibrium values before seemingly asymptoting to the full recovery state. To help understand this response, we develop a model that captures both the long development length and the second-order response of the turbulence, and we use a scale decomposition to connect the large-scale motions to the response behaviour.

Following the suggestion from the Monte–Carlo experiments in Jiménez (J. Turbul., 2020, doi:10.1080/14685248.2020.1742918) that dipoles are as important to the dynamics of decaying two-dimensional turbulence as individual vortex cores, it is found that the kinetic energy of this flow is carried by elongated streams formed by the concatenation of dipoles. Vortices separate into a family of small fast-moving cores, and another family of larger slowly moving ones, which can be described as ‘frozen’ into a slowly evolving ‘crystal.’ The kinematics of both families are very different, and only the former is self-similar. The latter is responsible for most of the kinetic energy of the flow, and its vortices form the dipoles and the streams. Mechanisms are discussed for the growth of this slow component.

Wind forcing injects energy into mesoscale eddies and near-inertial waves (NIWs) in the ocean, and the NIWs are believed to solve the puzzle of mesoscale energy budget by absorbing energy from mesoscale eddies. This work studies the turbulent energy transfer in the NIW–quasigeostrophic mean mesoscale eddy coupled system based on a previously derived two-dimensional model which inherits conserved quantities in Boussinesq equations (Xie & Vanneste, J. Fluid Mech., vol. 774, 2015, pp. 147–169). The conservation of energy, potential enstrophy and wave action implies the existence of phase transition with a change of the relative strength between NIW and mean-flow, quantified by a parameter 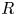$R$. By running forced-dissipative numerical simulations, we justify the existence of second-order phase transition around a critical value 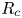$R_c$. When 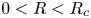$0<R<R_c$, energy transfers bidirectionally, wave action transfers downscale and vorticity forms strong cyclones. When 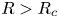$R>R_c$, energy transfers downscale, wave action transfers bidirectionally and vortex filaments are dominant. We find the catalytic wave induction mechanism where the NIW induces a downscale energy flux of the mean flow, which differs from the stimulated loss of balance mechanism observed in inertial value problems. In the parameter regime 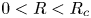$0<R<R_c$, catalytic wave induction is similar to the stimulated loss of balance as the downscale energy transfer is proportional to the NIW energy injection, however, catalytic wave induction has a distinct feature of the absence of energy conversion from mesoscale eddies to NIWs. The new mechanism is effective in the toy-model study, making it potentially important for ocean energetics.