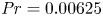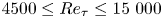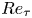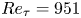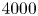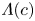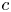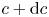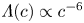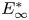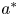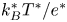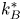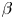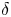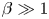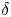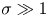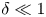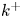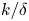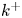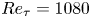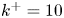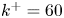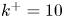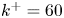doi:10.1017/jfm.2023.464 Salizzoni et al. Turbulent transfer and entrainment in a low-density jet
JFM Papers
Viscosity measurements of glycerol in a parallel-plate rheometer exposed to atmosphere
-
- Published online by Cambridge University Press:
- 26 July 2023, A2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Focus on Fluids
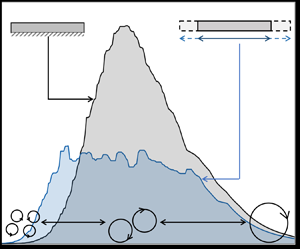
Towards a better understanding of granular flows
-
- Published online by Cambridge University Press:
- 26 July 2023, F1
-
- Article
-
- You have access
- HTML
- Export citation
JFM Rapids
An explicit representation for mean profiles and fluxes in forced passive scalar convection
-
- Published online by Cambridge University Press:
- 08 August 2023, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
JFM Papers
Swash flows generated by a train of solitary waves on a planar slope
-
- Published online by Cambridge University Press:
- 26 July 2023, A1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Richtmyer–Meshkov instability with a rippled reshock
-
- Published online by Cambridge University Press:
- 27 July 2023, A3
-
- Article
- Export citation
High-frequency instabilities in supersonic compression-ramp flow
-
- Published online by Cambridge University Press:
- 27 July 2023, A5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
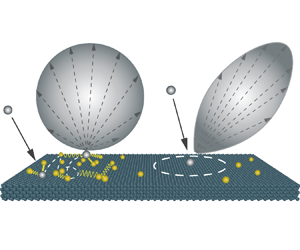
Impact of surface physisorption on gas scattering dynamics
-
- Published online by Cambridge University Press:
- 27 July 2023, A4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
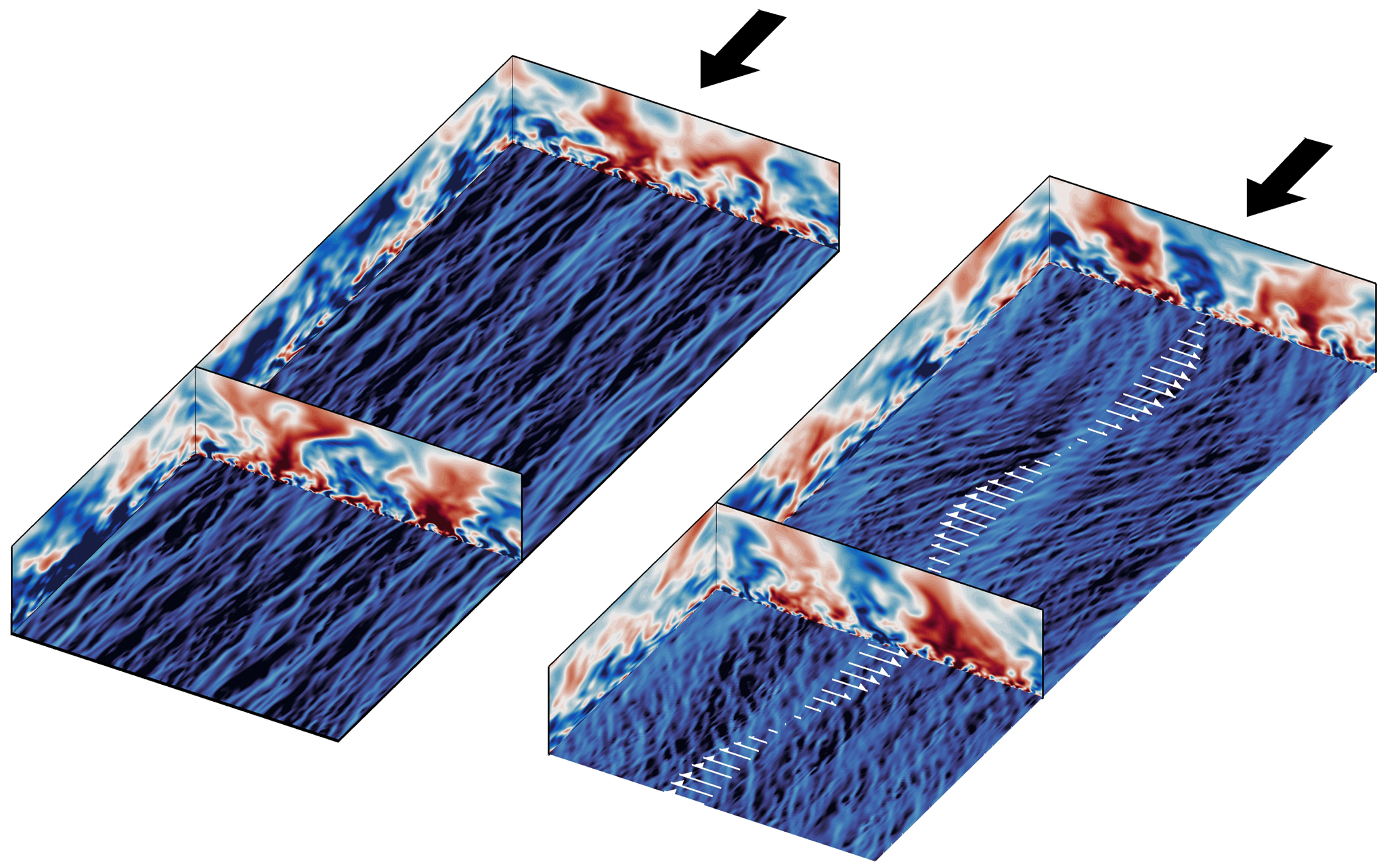
Turbulent drag reduction by spanwise wall forcing. Part 2. High-Reynolds-number experiments
-
- Published online by Cambridge University Press:
- 28 July 2023, A7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Turbulent drag reduction by spanwise wall forcing. Part 1. Large-eddy simulations
-
- Published online by Cambridge University Press:
- 28 July 2023, A6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Effects of wall vibrations on channel flows
-
- Published online by Cambridge University Press:
- 28 July 2023, A8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Close-contact melting of shear-thinning fluids
-
- Published online by Cambridge University Press:
- 28 July 2023, A9
-
- Article
- Export citation
A Perron–Frobenius analysis of wall-bounded turbulence
-
- Published online by Cambridge University Press:
- 28 July 2023, A10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Breaking wave field statistics with a multi-layer model
- Part of:
-
- Published online by Cambridge University Press:
- 31 July 2023, A12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Separate and joint clustering characteristics of large-Stokes-number sprays subjected to turbulent co-flows
-
- Published online by Cambridge University Press:
- 28 July 2023, A11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mean resolvent operator of a statistically steady flow
-
- Published online by Cambridge University Press:
- 31 July 2023, A13
-
- Article
- Export citation
Nonlinear electrophoretic velocity of a spherical colloidal particle
-
- Published online by Cambridge University Press:
- 31 July 2023, A14
-
- Article
- Export citation
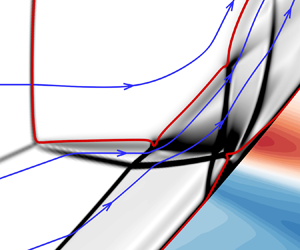
Modelling and shock control for a V-shaped blunt leading edge
-
- Published online by Cambridge University Press:
- 01 August 2023, A15
-
- Article
- Export citation
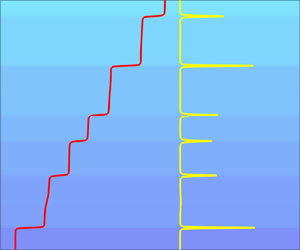
Salt fingering staircases and the three-component Phillips effect
-
- Published online by Cambridge University Press:
- 01 August 2023, A16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Attenuation of the unsteady loading on a high-rise building using top-surface open-loop control
-
- Published online by Cambridge University Press:
- 03 August 2023, A17
-
- Article
- Export citation
Outer-layer similarity and energy transfer in a rough-wall turbulent channel flow
-
- Published online by Cambridge University Press:
- 04 August 2023, A18
-
- Article
- Export citation