1. Introduction
Evaporation of droplets in inert gases occurs in a wide range of practical applications and have been investigated extensively since the pioneering work of Maxwell (Reference Maxwell1890). His approach of modelling the evaporation process based on macroscopic conservation laws assuming continuum liquid and gas phases has been proved adequate for sufficiently large droplets (i.e. Knudsen number ![]() ${{Kn}}=\lambda / a \ll 1$, where
${{Kn}}=\lambda / a \ll 1$, where ![]() $\lambda$ is the mean free path in the gas phase, and
$\lambda$ is the mean free path in the gas phase, and ![]() $a$ is the droplet diameter) and is now widely adopted. Over the years, continued efforts have been made to correct for some of the assumptions made by Maxwell, such as the quasi-steady (QS) gas phase, negligible internal and external flow (including the Stefan flow) and negligible droplet heating, as reviewed in detail in the literature (Sazhin Reference Sazhin2006; Sirignano Reference Sirignano2010). However, the paradoxical assumption of the local thermodynamic equilibrium at the interface (net evaporation can occur only when the interface region is out of equilibrium) persists and is still widely adopted in recent theoretical and experimental work (Lu et al. Reference Lu, Wilke, Preston, Kinefuchi, Chang-Davidson and Wang2017; Finneran, Garner & Nadal Reference Finneran, Garner and Nadal2021). The local thermodynamic equilibrium assumption allows for the determination of the vapour partial pressure in the close vicinity of the droplet surface (hence the vapour concentration), based on the liquid surface temperature. As a result, it serves as a sufficient boundary condition to couple the transport process in the liquid phase to those in the gas phase through a continuum hydrodynamic model without considering the non-equilibrium kinetics. This approach is adopted widely in the modelling the evaporation of isolated droplets (Sazhin Reference Sazhin2006; Sirignano Reference Sirignano2010; Holyst et al. Reference Holyst, Litniewski, Jakubczyk, Kolwas, Kolwas, Kowalski, Migacz, Palesa and Zientara2013a) and also droplets on an impermeable substrate (Deegan et al. Reference Deegan, Bakajin, Dupont, Huber, Nagel and Witten1997, Reference Deegan, Bakajin, Dupont, Huber, Nagel and Witten2000; Poulard, Be & Cazabat Reference Poulard, Be and Cazabat2003).
$a$ is the droplet diameter) and is now widely adopted. Over the years, continued efforts have been made to correct for some of the assumptions made by Maxwell, such as the quasi-steady (QS) gas phase, negligible internal and external flow (including the Stefan flow) and negligible droplet heating, as reviewed in detail in the literature (Sazhin Reference Sazhin2006; Sirignano Reference Sirignano2010). However, the paradoxical assumption of the local thermodynamic equilibrium at the interface (net evaporation can occur only when the interface region is out of equilibrium) persists and is still widely adopted in recent theoretical and experimental work (Lu et al. Reference Lu, Wilke, Preston, Kinefuchi, Chang-Davidson and Wang2017; Finneran, Garner & Nadal Reference Finneran, Garner and Nadal2021). The local thermodynamic equilibrium assumption allows for the determination of the vapour partial pressure in the close vicinity of the droplet surface (hence the vapour concentration), based on the liquid surface temperature. As a result, it serves as a sufficient boundary condition to couple the transport process in the liquid phase to those in the gas phase through a continuum hydrodynamic model without considering the non-equilibrium kinetics. This approach is adopted widely in the modelling the evaporation of isolated droplets (Sazhin Reference Sazhin2006; Sirignano Reference Sirignano2010; Holyst et al. Reference Holyst, Litniewski, Jakubczyk, Kolwas, Kolwas, Kowalski, Migacz, Palesa and Zientara2013a) and also droplets on an impermeable substrate (Deegan et al. Reference Deegan, Bakajin, Dupont, Huber, Nagel and Witten1997, Reference Deegan, Bakajin, Dupont, Huber, Nagel and Witten2000; Poulard, Be & Cazabat Reference Poulard, Be and Cazabat2003).
Meanwhile, in experimental and theoretical work dealing with evaporation of droplets in their own vapour (Lu et al. Reference Lu, Kinefuchi, Wilke, Vaartstra and Wang2019; Rana, Lockerby & Sprittles Reference Rana, Lockerby and Sprittles2019), the local thermodynamic equilibrium is replaced by a more rigorous out-of-equilibrium kinetic boundary condition where the evaporative mass flux ![]() $J$ depends on the difference in the chemical potential between the liquid and the vapour phase. This kinetic boundary condition enables the decoupling of the low Mach number gas phase from the liquid phase, so a ‘one-sided’ model can be developed to model the liquid evaporation dynamics. Due to this convenience, the one-sided model was also used frequently in modelling the dynamics of an evaporating liquid film (Burelbach, Bankoff & Davis Reference Burelbach, Bankoff and Davis1988; Oron, Davis & Bankoff Reference Oron, Davis and Bankoff1997; Craster & Matar Reference Craster and Matar2009). Assuming the evaporative mass flux across the out-of-equilibrium kinetic region – i.e. the Knudsen layer – should equal the mass flux out of this region, a mixed kinetic-diffusion boundary condition can be formulated to couple the liquid and gas phases (Kryukov, Levashov & Sazhin Reference Kryukov, Levashov and Sazhin2004; Sultan, Boudaoud & Ben Amar Reference Sultan, Boudaoud and Ben Amar2005; Holyst et al. Reference Holyst, Litniewski, Jakubczyk, Kolwas, Kolwas, Kowalski, Migacz, Palesa and Zientara2013a). Sultan et al. (Reference Sultan, Boudaoud and Ben Amar2005) also identified the kinetic Péclet number
$J$ depends on the difference in the chemical potential between the liquid and the vapour phase. This kinetic boundary condition enables the decoupling of the low Mach number gas phase from the liquid phase, so a ‘one-sided’ model can be developed to model the liquid evaporation dynamics. Due to this convenience, the one-sided model was also used frequently in modelling the dynamics of an evaporating liquid film (Burelbach, Bankoff & Davis Reference Burelbach, Bankoff and Davis1988; Oron, Davis & Bankoff Reference Oron, Davis and Bankoff1997; Craster & Matar Reference Craster and Matar2009). Assuming the evaporative mass flux across the out-of-equilibrium kinetic region – i.e. the Knudsen layer – should equal the mass flux out of this region, a mixed kinetic-diffusion boundary condition can be formulated to couple the liquid and gas phases (Kryukov, Levashov & Sazhin Reference Kryukov, Levashov and Sazhin2004; Sultan, Boudaoud & Ben Amar Reference Sultan, Boudaoud and Ben Amar2005; Holyst et al. Reference Holyst, Litniewski, Jakubczyk, Kolwas, Kolwas, Kowalski, Migacz, Palesa and Zientara2013a). Sultan et al. (Reference Sultan, Boudaoud and Ben Amar2005) also identified the kinetic Péclet number ![]() ${{Pe}_k} = u_k H/\mathcal {D}_{AB}$ (where
${{Pe}_k} = u_k H/\mathcal {D}_{AB}$ (where ![]() $u_k$ is the typical kinetic velocity,
$u_k$ is the typical kinetic velocity, ![]() $H$ is the characteristic length and
$H$ is the characteristic length and ![]() $\mathcal {D}_{AB}$ is the mass diffusivity between the liquid
$\mathcal {D}_{AB}$ is the mass diffusivity between the liquid ![]() $A$ and the inert gas
$A$ and the inert gas ![]() $B$) to be the key dimensionless group, and showed that the local thermodynamic equilibrium assumption corresponds to the limiting case of an infinitely large
$B$) to be the key dimensionless group, and showed that the local thermodynamic equilibrium assumption corresponds to the limiting case of an infinitely large ![]() ${{Pe}_k}$. When formulating the boundary condition, existing works focused on slow evaporation (thus ignoring the Stefan flow) and adopted the widely used Hertz–Knudsen (HK) relation (Knudsen Reference Knudsen1950) – i.e. (1.1) – to model the kinetics of net evaporation
${{Pe}_k}$. When formulating the boundary condition, existing works focused on slow evaporation (thus ignoring the Stefan flow) and adopted the widely used Hertz–Knudsen (HK) relation (Knudsen Reference Knudsen1950) – i.e. (1.1) – to model the kinetics of net evaporation
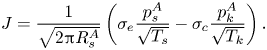 \begin{equation} J = \frac{1}{\sqrt{2{\rm \pi} R_s^A}}\left(\sigma_e \frac{p_s^A}{\sqrt{T_s}} - \sigma_c \frac{p_k^A}{\sqrt{T_k}}\right). \end{equation}
\begin{equation} J = \frac{1}{\sqrt{2{\rm \pi} R_s^A}}\left(\sigma_e \frac{p_s^A}{\sqrt{T_s}} - \sigma_c \frac{p_k^A}{\sqrt{T_k}}\right). \end{equation}
In this expression, ![]() $\sigma _e$ and
$\sigma _e$ and ![]() $\sigma _c$ are empirical evaporation and condensation coefficients,
$\sigma _c$ are empirical evaporation and condensation coefficients, ![]() $(p_s^A,T_s)$ and
$(p_s^A,T_s)$ and ![]() $(p_k^A,T_k)$ are the vapour pressure of species
$(p_k^A,T_k)$ are the vapour pressure of species ![]() $A$ and temperature on the liquid surface and just outside the Knudsen layer, respectively, and
$A$ and temperature on the liquid surface and just outside the Knudsen layer, respectively, and ![]() $R_s^A$ is the specific gas constant of species
$R_s^A$ is the specific gas constant of species ![]() $A$. The HK relation was originally derived based on the assumption of an equilibrium Maxwellian velocity distribution in the gas phase and decoupled evaporation and condensation processes (i.e.
$A$. The HK relation was originally derived based on the assumption of an equilibrium Maxwellian velocity distribution in the gas phase and decoupled evaporation and condensation processes (i.e. ![]() $\sigma _e$ and
$\sigma _e$ and ![]() $\sigma _c$ are constants). The HK relation is considered as semi-empirical, due to the absence of explicit expressions for
$\sigma _c$ are constants). The HK relation is considered as semi-empirical, due to the absence of explicit expressions for ![]() $\sigma _e$ and
$\sigma _e$ and ![]() $\sigma _c$. Analytical expressions for
$\sigma _c$. Analytical expressions for ![]() $\sigma _e$ and
$\sigma _e$ and ![]() $\sigma _c$ based on the statistical rate theory in the thermal-energy-dominated limit (TED-SRT) were recently proposed by Persad & Ward (Reference Persad and Ward2016), as shown in (1.2a,b) and (1.3a–c)
$\sigma _c$ based on the statistical rate theory in the thermal-energy-dominated limit (TED-SRT) were recently proposed by Persad & Ward (Reference Persad and Ward2016), as shown in (1.2a,b) and (1.3a–c)
where
In these expressions, ![]() $N$ is the number of internal vibration degrees of freedom (which is
$N$ is the number of internal vibration degrees of freedom (which is ![]() $3n-6$ for nonlinear molecules consisting of
$3n-6$ for nonlinear molecules consisting of ![]() $n$ atoms and
$n$ atoms and ![]() $3n-5$ for linear molecules). Experimental data reviewed by Persad & Ward (Reference Persad and Ward2016) suggest that
$3n-5$ for linear molecules). Experimental data reviewed by Persad & Ward (Reference Persad and Ward2016) suggest that ![]() $\overline {\delta T}$ is typically much smaller than unity, so that
$\overline {\delta T}$ is typically much smaller than unity, so that ![]() $\hat {\sigma }_e$ and
$\hat {\sigma }_e$ and ![]() $\sigma _c$ can be linearised about
$\sigma _c$ can be linearised about ![]() $\overline {T_k}=1$, which yields
$\overline {T_k}=1$, which yields ![]() $\hat {\sigma }_e = 1 + O(\overline {\delta T}^2)$ and
$\hat {\sigma }_e = 1 + O(\overline {\delta T}^2)$ and ![]() $\sigma _c = 1 + \overline {\delta T}/2 + O(\overline {\delta T}^2)$. The TED-SRT formulation shows that both
$\sigma _c = 1 + \overline {\delta T}/2 + O(\overline {\delta T}^2)$. The TED-SRT formulation shows that both ![]() $\sigma _e$ and
$\sigma _e$ and ![]() $\sigma _c$ are explicit functions of
$\sigma _c$ are explicit functions of ![]() $p_s$,
$p_s$, ![]() $T_s$,
$T_s$, ![]() $p_k$ and
$p_k$ and ![]() $T_k$, so that the evaporation and condensation processes are coupled. As highlighted by Persad & Ward (Reference Persad and Ward2016), considering
$T_k$, so that the evaporation and condensation processes are coupled. As highlighted by Persad & Ward (Reference Persad and Ward2016), considering ![]() $T_k$ is always larger than
$T_k$ is always larger than ![]() $T_s$ in cases of net evaporation, it is clear that
$T_s$ in cases of net evaporation, it is clear that ![]() $\sigma _c > 1$ during the evaporation. Therefore, the conventional interpretation that
$\sigma _c > 1$ during the evaporation. Therefore, the conventional interpretation that ![]() $\sigma _c$ represents the fraction of molecules condensed into liquid on reaching the liquid surface is not physically sound. Sultan et al. (Reference Sultan, Boudaoud and Ben Amar2005) set
$\sigma _c$ represents the fraction of molecules condensed into liquid on reaching the liquid surface is not physically sound. Sultan et al. (Reference Sultan, Boudaoud and Ben Amar2005) set ![]() $\sigma _e = \sigma _c = 1$ and
$\sigma _e = \sigma _c = 1$ and ![]() $T_s = T_k$ (a common approach adopted in the literature) which de facto implies thermodynamic equilibrium in the Knudsen layer (Persad & Ward Reference Persad and Ward2016). In addition, in (1.1),
$T_s = T_k$ (a common approach adopted in the literature) which de facto implies thermodynamic equilibrium in the Knudsen layer (Persad & Ward Reference Persad and Ward2016). In addition, in (1.1), ![]() $p_s$ is commonly taken to be the saturated pressure
$p_s$ is commonly taken to be the saturated pressure ![]() $p_s^\star$ of the pure substance without correcting for its change due to the presence of inert gases. The impact of adopting this mixed boundary condition and relevant simplifications on predicting the evaporation rate of a droplet has yet to be quantified.
$p_s^\star$ of the pure substance without correcting for its change due to the presence of inert gases. The impact of adopting this mixed boundary condition and relevant simplifications on predicting the evaporation rate of a droplet has yet to be quantified.
In this work, we derive more general mixed kinetic-diffusion boundary conditions that take into account the Stefan flow (§ 2). The mixed boundary condition is formulated based on either the semi-empirical HK model or the analytical TED-SRT model and includes corrections for the change of liquid chemical potential due to the presence of inert gas and the temperature jump across the Knudsen layer. The mixed boundary condition is then applied to investigate the problem of QS evaporation of a spherical droplet in an infinite domain containing inert gases. The full and linearised solutions for the QS evaporation problem are presented in § 3. The analytical and numerical results are then compared with the experimental data reported in the literature. The comparison shows the potential errors caused by the local thermodynamic equilibrium assumption and the neglect of the change of the chemical potential of the liquid phase (i.e. the effect of the inert gas). Conclusions regarding the impact of such a generalised mixed kinetic-diffusion boundary condition on the evaporation rate, and future work, are presented in the final section.
2. Formulation of the mixed boundary conditions
We consider here a spherical droplet of size ![]() $a$ of pure substance
$a$ of pure substance ![]() $A$ evaporating in an infinite gas domain that consists of vapour
$A$ evaporating in an infinite gas domain that consists of vapour ![]() $A$ and inert immiscible gases
$A$ and inert immiscible gases ![]() $B$, as in figure 1. When required, partial properties of a pure substances (e.g. evaporating substance
$B$, as in figure 1. When required, partial properties of a pure substances (e.g. evaporating substance ![]() $A$ or inert gas
$A$ or inert gas ![]() $B$) are denoted using superscripts
$B$) are denoted using superscripts ![]() $A$ and
$A$ and ![]() $B$, respectively, whereas properties of the whole gas phase (i.e. the mixture of gaseous
$B$, respectively, whereas properties of the whole gas phase (i.e. the mixture of gaseous ![]() $A$ and the inert gas
$A$ and the inert gas ![]() $B$) have no superscript. Throughout the article, the superscript
$B$) have no superscript. Throughout the article, the superscript ![]() $l$ stands for the liquid domain. All quantities evaluated at the liquid interface and just outside the Knudsen layer are labelled with subscripts
$l$ stands for the liquid domain. All quantities evaluated at the liquid interface and just outside the Knudsen layer are labelled with subscripts ![]() $s$ and
$s$ and ![]() $k$, respectively.
$k$, respectively.
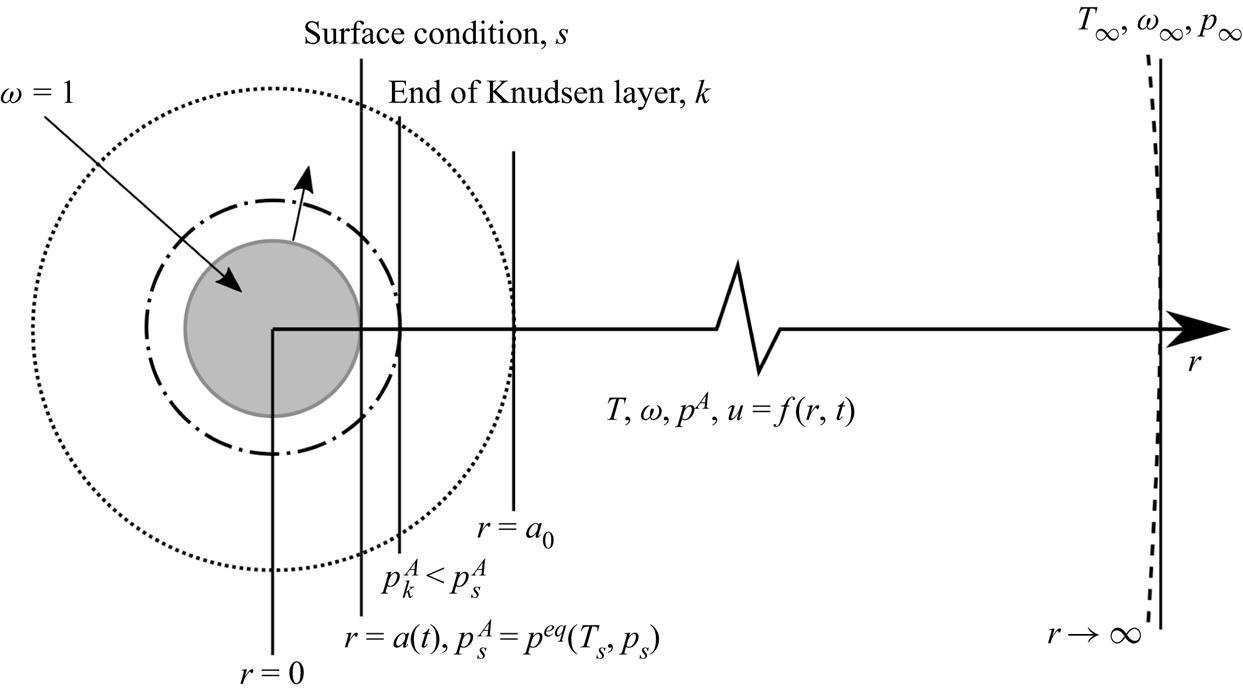
Figure 1. Illustration of the evaporation of a droplet in an infinite gas domain. Note that the Knudsen layer represents the conceptual out-of-equilibrium kinetic region: its outer boundary is not sharp due to the continuity of the partial pressure and temperature.
2.1. Mass conservation across the Knudsen layer
Assuming an infinitely thin Knudsen layer, mass conservation requires that
where ![]() $\rho$ is the density,
$\rho$ is the density, ![]() $\boldsymbol {u}$ is the velocity and
$\boldsymbol {u}$ is the velocity and ![]() $\hat {\boldsymbol {n}}$ is the normal outward unit vector. The immiscibility of
$\hat {\boldsymbol {n}}$ is the normal outward unit vector. The immiscibility of ![]() $B$ in
$B$ in ![]() $A$ results in a vanishing mass flux of
$A$ results in a vanishing mass flux of ![]() $B$ across the interface, such that the evaporation mass flux equals the mass diffusion flux of
$B$ across the interface, such that the evaporation mass flux equals the mass diffusion flux of ![]() $A$, which can be written as
$A$, which can be written as
where ![]() $\omega$ is the mass fraction of
$\omega$ is the mass fraction of ![]() $A$, and
$A$, and ![]() $\varPhi = 1 - \omega$. Here, we consider the case where the total pressure in the gas domain remains unchanged (i.e.
$\varPhi = 1 - \omega$. Here, we consider the case where the total pressure in the gas domain remains unchanged (i.e. ![]() ${Ma} \ll 1$). In the case of high Mach number, the pressure relaxation process in the gas domain needs to be accounted for to find the change in pressure. To proceed, a kinetic model within the Knudsen layer (e.g. the analytical TED-SRT model or the semi-empirical HK model) needs to be used to predict
${Ma} \ll 1$). In the case of high Mach number, the pressure relaxation process in the gas domain needs to be accounted for to find the change in pressure. To proceed, a kinetic model within the Knudsen layer (e.g. the analytical TED-SRT model or the semi-empirical HK model) needs to be used to predict ![]() $J$.
$J$.
2.2. The HK-based mixed boundary condition
Assuming that the Knudsen layer is not too far from thermodynamic equilibrium and the velocity profile in the gas domain is Maxwellian, Struchtrup et al. (Reference Struchtrup, Beckmann, Rana and Frezzotti2017) proposed the following kinetic model in a pure vapour environment, based on the extension of the Onsager–Casimir reciprocity relations:
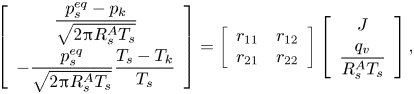 \begin{equation} \left[ \begin{array}{c} \dfrac{p_s^{eq}-p_k}{\sqrt{2 {\rm \pi}R_s^A T_s}} \\[10pt] -\dfrac{p_s^{eq}}{\sqrt{2 {\rm \pi}R_s^A T_s}} \dfrac{T_s-T_k}{T_s} \end{array} \right] = \left[ \begin{array}{cc} r_{11} & r_{12} \\ r_{21} & r_{22} \end{array}\right] \left[ \begin{array}{c} J \\[4pt] \dfrac{q_v}{R_s^A T_s} \end{array} \right], \end{equation}
\begin{equation} \left[ \begin{array}{c} \dfrac{p_s^{eq}-p_k}{\sqrt{2 {\rm \pi}R_s^A T_s}} \\[10pt] -\dfrac{p_s^{eq}}{\sqrt{2 {\rm \pi}R_s^A T_s}} \dfrac{T_s-T_k}{T_s} \end{array} \right] = \left[ \begin{array}{cc} r_{11} & r_{12} \\ r_{21} & r_{22} \end{array}\right] \left[ \begin{array}{c} J \\[4pt] \dfrac{q_v}{R_s^A T_s} \end{array} \right], \end{equation}
where coefficients ![]() $r_{11}=1/{\rm \pi} +9/32$,
$r_{11}=1/{\rm \pi} +9/32$, ![]() $r_{12}=r_{21}=1/16+1/(5{\rm \pi} )$,
$r_{12}=r_{21}=1/16+1/(5{\rm \pi} )$, ![]() $r_{22}=1/8+13/(25{\rm \pi} )$,
$r_{22}=1/8+13/(25{\rm \pi} )$, ![]() $p_s^{eq}$ is the equilibrium vapour pressure of species
$p_s^{eq}$ is the equilibrium vapour pressure of species ![]() $A$ and
$A$ and ![]() $q_v$ is the heat flux adds to the vapour. In the case of a negligible change of sensible heat inside the droplet,
$q_v$ is the heat flux adds to the vapour. In the case of a negligible change of sensible heat inside the droplet, ![]() $q_v=-J \mathcal {L}$, where
$q_v=-J \mathcal {L}$, where ![]() $\mathcal {L}$ is the latent heat of evaporation. The above expression is an extension of the HK model taking into account the Stefan flow due to net evaporation, with the additional assumption
$\mathcal {L}$ is the latent heat of evaporation. The above expression is an extension of the HK model taking into account the Stefan flow due to net evaporation, with the additional assumption ![]() $\sigma _e=\sigma _c=1$. It also predicts the temperature jump across the Knudsen layer, which is commonly ignored in the literature. As shown by Persad & Ward (Reference Persad and Ward2016), assuming either
$\sigma _e=\sigma _c=1$. It also predicts the temperature jump across the Knudsen layer, which is commonly ignored in the literature. As shown by Persad & Ward (Reference Persad and Ward2016), assuming either ![]() $T_k = T_s$ or
$T_k = T_s$ or ![]() $\sigma _e = \sigma _c$ does not introduce major discrepancies compared with experimental results (
$\sigma _e = \sigma _c$ does not introduce major discrepancies compared with experimental results (![]() ${\leqslant }5\,\%$), but making both assumptions simultaneously forces the Knudsen layer into equilibrium, which could lead to significant errors. When applied in an inert gas environment, while the form of (2.3) might hold as long as the Knudsen layer is not too far from equilibrium, i.e. a linear irreversible process, the coefficients and
${\leqslant }5\,\%$), but making both assumptions simultaneously forces the Knudsen layer into equilibrium, which could lead to significant errors. When applied in an inert gas environment, while the form of (2.3) might hold as long as the Knudsen layer is not too far from equilibrium, i.e. a linear irreversible process, the coefficients and ![]() $p_s^{eq}$ should be corrected by taking into account inert gases. The effect of inert gases on the temperature jump is evidenced by the empirical correlation (2.4) proposed by Holyst et al. (Reference Holyst, Litniewski, Jakubczyk, Zientara and Woźniak2013b). Equation (2.4) is based on curve fitting of data obtained from molecular dynamic (MD) simulations of the evaporation of a droplet made of a Lennard–Jones fluid in inert gases and reads as
$p_s^{eq}$ should be corrected by taking into account inert gases. The effect of inert gases on the temperature jump is evidenced by the empirical correlation (2.4) proposed by Holyst et al. (Reference Holyst, Litniewski, Jakubczyk, Zientara and Woźniak2013b). Equation (2.4) is based on curve fitting of data obtained from molecular dynamic (MD) simulations of the evaporation of a droplet made of a Lennard–Jones fluid in inert gases and reads as
where ![]() $C$ is a fitting parameter calculated to be 2.35, and
$C$ is a fitting parameter calculated to be 2.35, and ![]() $\lambda$ is the mean free path of inert gas molecules. Equation (2.4) shows that a smaller
$\lambda$ is the mean free path of inert gas molecules. Equation (2.4) shows that a smaller ![]() $\lambda$ leads to a smaller temperature jump. This makes sense because the thermalisation process becomes more efficient as the collision frequency increases at reduced
$\lambda$ leads to a smaller temperature jump. This makes sense because the thermalisation process becomes more efficient as the collision frequency increases at reduced ![]() $\lambda$.
$\lambda$.
When the liquid surface is assumed to be at thermodynamic equilibrium, ![]() $p_s^{eq}$ can be determined by equating the chemical potential of the liquid phase
$p_s^{eq}$ can be determined by equating the chemical potential of the liquid phase ![]() $\mu ^l$ and that of the vapour phase
$\mu ^l$ and that of the vapour phase ![]() $\mu ^v$. In order to find the change of chemical potential due to the presence of inert gases, we consider an isothermal gas addition process. The chemical potentials of the liquid phase and vapour phase of
$\mu ^v$. In order to find the change of chemical potential due to the presence of inert gases, we consider an isothermal gas addition process. The chemical potentials of the liquid phase and vapour phase of ![]() $A$ in the absence of any inert gas at temperature
$A$ in the absence of any inert gas at temperature ![]() $T_s$ and pressure
$T_s$ and pressure ![]() $p_s^\star$ are denoted by
$p_s^\star$ are denoted by ![]() $\mu ^{l\star }$ and
$\mu ^{l\star }$ and ![]() $\mu ^{v\star }$. As the inert gas is added to the system to reach a new equilibrium at increased total pressure
$\mu ^{v\star }$. As the inert gas is added to the system to reach a new equilibrium at increased total pressure ![]() $p_s$, one obtains
$p_s$, one obtains
Applying the Gibbs–Duhem equation yields
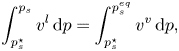 \begin{equation} \int_{p_s^\star}^{p_s} v^l\,{\rm d}p = \int_{p_s^\star}^{p_s^{eq}} v^v\,{\rm d}p, \end{equation}
\begin{equation} \int_{p_s^\star}^{p_s} v^l\,{\rm d}p = \int_{p_s^\star}^{p_s^{eq}} v^v\,{\rm d}p, \end{equation}
where ![]() $v^l$,
$v^l$, ![]() $v^v$ and
$v^v$ and ![]() $v^{v\star }$ are molar volume of
$v^{v\star }$ are molar volume of ![]() $A$ in liquid phase, and the vapour phase with and without inert gas, respectively. In the case of constant liquid molar volume and ideal gases, one obtains
$A$ in liquid phase, and the vapour phase with and without inert gas, respectively. In the case of constant liquid molar volume and ideal gases, one obtains
It appears from (2.7) that the exponential correction factor could become significant as the specific volume ratio increases, e.g. at high system pressure or low gas temperature. Note that the assumption of ideal gas needs to be corrected at high pressure or very low temperature. To assess the value of ![]() $p_s^\star$, the Clausius–Claperon equation – which is derived assuming (i) an ideal gas law, (ii) negligibly small gas phase density (compared with that of the liquid phase) and (iii) constant latent heat – can be integrated between the local equilibrium conditions at far field (i.e. outside the boundary layer) and that at the liquid surface. One obtains
$p_s^\star$, the Clausius–Claperon equation – which is derived assuming (i) an ideal gas law, (ii) negligibly small gas phase density (compared with that of the liquid phase) and (iii) constant latent heat – can be integrated between the local equilibrium conditions at far field (i.e. outside the boundary layer) and that at the liquid surface. One obtains
where all properties at infinity are labelled with the subscript ![]() $\infty$. In the previous expression,
$\infty$. In the previous expression, ![]() $T_{\infty }^{sat}$ is the saturated temperature at
$T_{\infty }^{sat}$ is the saturated temperature at ![]() $p_\infty$.
$p_\infty$.
By combining (2.2), (2.3), (2.7) and (2.8), and accounting for the surface tension ![]() $\sigma _T$ based on Kelvin's law, we obtain the following mixed kinetic-diffusion boundary condition based on HK model:
$\sigma _T$ based on Kelvin's law, we obtain the following mixed kinetic-diffusion boundary condition based on HK model:
 \begin{align} &\sqrt{\frac{1}{2{\rm \pi} R_s^A T_s}}\left\{c_1 p_{\infty} \exp\left[\frac{\mathcal{L}}{R_s^A}\left(\frac{1}{ T_{\infty}^{sat}}-\frac{1}{T_s}\right)+\overline{v_s}+\frac{\bar{\sigma}}{a}\right]-\left(c_1+c_2 \overline{\Delta T}\right)p_k^A \right\}\nonumber\\ &\quad = \frac{\rho_k\mathcal{D}_{AB} [\boldsymbol{\nabla}\varPhi \boldsymbol{\cdot} \hat{\boldsymbol{n}}]_k}{\varPhi_k}, \end{align}
\begin{align} &\sqrt{\frac{1}{2{\rm \pi} R_s^A T_s}}\left\{c_1 p_{\infty} \exp\left[\frac{\mathcal{L}}{R_s^A}\left(\frac{1}{ T_{\infty}^{sat}}-\frac{1}{T_s}\right)+\overline{v_s}+\frac{\bar{\sigma}}{a}\right]-\left(c_1+c_2 \overline{\Delta T}\right)p_k^A \right\}\nonumber\\ &\quad = \frac{\rho_k\mathcal{D}_{AB} [\boldsymbol{\nabla}\varPhi \boldsymbol{\cdot} \hat{\boldsymbol{n}}]_k}{\varPhi_k}, \end{align}
where ![]() $c_1=r_{22}/(r_{11}r_{22}-r_{12}^2)$,
$c_1=r_{22}/(r_{11}r_{22}-r_{12}^2)$, ![]() $c_2=c_1 r_{11}/r_{22}$ and
$c_2=c_1 r_{11}/r_{22}$ and ![]() $\bar {\sigma } = 2\sigma _T/(R_s^A T^l \rho ^l)$.
$\bar {\sigma } = 2\sigma _T/(R_s^A T^l \rho ^l)$.
2.3. The TED-SRT-based mixed boundary condition
Combining the analytical TED-SRT formulation derived by Persad & Ward (Reference Persad and Ward2016), i.e. (1.2a,b), together with (2.2), (2.7) and (2.8), and accounting for the surface tension, the following mixed boundary conditions can be derived:
 \begin{equation} \sqrt{\frac{1}{2{\rm \pi} R_s^A}}\left\{\hat{\sigma}_e\frac{\left\{p_{\infty} \exp\left[\dfrac{\mathcal{L}}{R_s^A}\left(\dfrac{1}{T_{\infty}^{sat}}-\dfrac{1}{T_s}\right)+ \overline{v_s}+\frac{\bar{\sigma}}{a}\right]\right\}^2}{p_k^A\sqrt{T_s}}-\sigma_c \frac{p_k^A}{\sqrt{T_k}}\right\} = \frac{\rho_k\mathcal{D}_{AB} [\boldsymbol{\nabla}\varPhi \boldsymbol{\cdot} \hat{\boldsymbol{n}}]_k}{\varPhi_k}. \end{equation}
\begin{equation} \sqrt{\frac{1}{2{\rm \pi} R_s^A}}\left\{\hat{\sigma}_e\frac{\left\{p_{\infty} \exp\left[\dfrac{\mathcal{L}}{R_s^A}\left(\dfrac{1}{T_{\infty}^{sat}}-\dfrac{1}{T_s}\right)+ \overline{v_s}+\frac{\bar{\sigma}}{a}\right]\right\}^2}{p_k^A\sqrt{T_s}}-\sigma_c \frac{p_k^A}{\sqrt{T_k}}\right\} = \frac{\rho_k\mathcal{D}_{AB} [\boldsymbol{\nabla}\varPhi \boldsymbol{\cdot} \hat{\boldsymbol{n}}]_k}{\varPhi_k}. \end{equation}2.4. Dimensionless forms of the mixed boundary conditions
To make the mixed kinetic-diffusion boundary conditions (2.9) and (2.10) dimensionless, the initial droplet radius ![]() $a_0$, the initial Stefan flow gas velocity
$a_0$, the initial Stefan flow gas velocity ![]() $\mathcal {D}_{AB}/a_0$ and the quantity
$\mathcal {D}_{AB}/a_0$ and the quantity ![]() $a_0^2/\mathcal {D}_{AB}$ are chosen as the typical length, velocity and time, respectively. The quantity
$a_0^2/\mathcal {D}_{AB}$ are chosen as the typical length, velocity and time, respectively. The quantity ![]() $\rho _\infty$ is chosen as the typical gas density, such that the typical evaporative mass flux becomes
$\rho _\infty$ is chosen as the typical gas density, such that the typical evaporative mass flux becomes ![]() $\rho _\infty \mathcal {D}_{AB}/a_0$.
$\rho _\infty \mathcal {D}_{AB}/a_0$.
The mixed boundary condition based on the TED-SRT model (2.10) can be written in a dimensionless form as
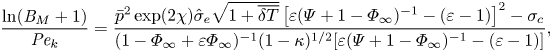 \begin{equation} \frac{\ln({{B}_M} + 1)}{{{Pe}_k}}=\frac{\bar{p}^2\exp(2\chi) \hat{\sigma}_e\sqrt{1+\overline{\delta T}}\left[\varepsilon(\varPsi+1-\varPhi_\infty)^{{-}1}-(\varepsilon-1)\right]^2-\sigma_c}{(1-\varPhi_\infty + \varepsilon\varPhi_\infty)^{{-}1}(1-\kappa)^{1/2}[\varepsilon(\varPsi+1-\varPhi_\infty)^{{-}1}-(\varepsilon-1)]}, \end{equation}
\begin{equation} \frac{\ln({{B}_M} + 1)}{{{Pe}_k}}=\frac{\bar{p}^2\exp(2\chi) \hat{\sigma}_e\sqrt{1+\overline{\delta T}}\left[\varepsilon(\varPsi+1-\varPhi_\infty)^{{-}1}-(\varepsilon-1)\right]^2-\sigma_c}{(1-\varPhi_\infty + \varepsilon\varPhi_\infty)^{{-}1}(1-\kappa)^{1/2}[\varepsilon(\varPsi+1-\varPhi_\infty)^{{-}1}-(\varepsilon-1)]}, \end{equation}where
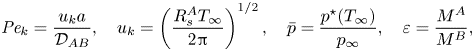 $$\begin{gather}{{Pe}_k} = \frac{u_k a}{\mathcal{D}_{AB}},\quad u_k=\left(\frac{ R_s^A T_\infty}{2{\rm \pi}}\right)^{1/2},\quad \bar{p}=\frac{p^{{\star}}(T_\infty)}{p_\infty}, \quad \varepsilon=\frac{M^A}{M^B}, \end{gather}$$
$$\begin{gather}{{Pe}_k} = \frac{u_k a}{\mathcal{D}_{AB}},\quad u_k=\left(\frac{ R_s^A T_\infty}{2{\rm \pi}}\right)^{1/2},\quad \bar{p}=\frac{p^{{\star}}(T_\infty)}{p_\infty}, \quad \varepsilon=\frac{M^A}{M^B}, \end{gather}$$
In the above expressions, ![]() $\gamma$ is the specific heat capacity ratio,
$\gamma$ is the specific heat capacity ratio, ![]() $c_p$ is the specific heat capacity,
$c_p$ is the specific heat capacity, ![]() ${{Ja}}$ is the Jakob number,
${{Ja}}$ is the Jakob number, ![]() ${{B}_M}$ and
${{B}_M}$ and ![]() ${{B}_T}$ are the Spalding heat and mass transfer numbers, respectively, and
${{B}_T}$ are the Spalding heat and mass transfer numbers, respectively, and ![]() $T_{QS,k}$ and
$T_{QS,k}$ and ![]() $\omega _{QS,k}$ are the temperature and mass fraction obtained from the QS solutions.
$\omega _{QS,k}$ are the temperature and mass fraction obtained from the QS solutions.
The mixed boundary condition based on the HK formulation (2.9) can also be made dimensionless in the same way, which yields
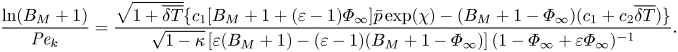 \begin{align} \frac{\ln(B_M+1)}{{{Pe}_k}}=\frac{\sqrt{1+\overline{\delta T}}\{c_1[B_M+1+(\varepsilon-1)\varPhi_\infty]\bar{p}\exp(\chi) - (B_M+1-\varPhi_\infty)(c_1+c_2\overline{\delta T})\}}{\sqrt{1-\kappa}\left[\varepsilon(B_M+1)-(\varepsilon-1)(B_M+1-\varPhi_\infty)\right]( 1-\varPhi_\infty+\varepsilon \varPhi_\infty)^{{-}1}}. \end{align}
\begin{align} \frac{\ln(B_M+1)}{{{Pe}_k}}=\frac{\sqrt{1+\overline{\delta T}}\{c_1[B_M+1+(\varepsilon-1)\varPhi_\infty]\bar{p}\exp(\chi) - (B_M+1-\varPhi_\infty)(c_1+c_2\overline{\delta T})\}}{\sqrt{1-\kappa}\left[\varepsilon(B_M+1)-(\varepsilon-1)(B_M+1-\varPhi_\infty)\right]( 1-\varPhi_\infty+\varepsilon \varPhi_\infty)^{{-}1}}. \end{align}Similarly, the analytical temperature jump model developed for evaporation in the pure vapour environment, i.e. (2.3) can be non-dimensionalised to become
The empirical temperature jump model proposed for the evaporation in inert gases, i.e. (2.4), can be recast dimensionlessly as
Both (2.11) and (2.13) show that the validity of the assumption of local thermodynamic equilibrium depends on the value of ![]() ${{Pe}_k}$. As
${{Pe}_k}$. As ![]() ${{Pe}_k} \rightarrow \infty$, the infinitely fast kinetic convection process instantaneously smooths out any imbalance in the chemical potential difference across the Knudsen layer – i.e. left-hand sides of (2.11) and (2.13)
${{Pe}_k} \rightarrow \infty$, the infinitely fast kinetic convection process instantaneously smooths out any imbalance in the chemical potential difference across the Knudsen layer – i.e. left-hand sides of (2.11) and (2.13) ![]() $\rightarrow 0$ – so the Knudsen layer will instantaneously be in thermodynamic equilibrium. The evaporation rate is then limited by the mass diffusion of
$\rightarrow 0$ – so the Knudsen layer will instantaneously be in thermodynamic equilibrium. The evaporation rate is then limited by the mass diffusion of ![]() $A$ out from the Knudsen layer. One can also see from (2.14) that
$A$ out from the Knudsen layer. One can also see from (2.14) that ![]() $\overline {\delta T} \rightarrow 0$ as
$\overline {\delta T} \rightarrow 0$ as ![]() ${{Pe}_k} \rightarrow \infty$. When
${{Pe}_k} \rightarrow \infty$. When ![]() ${{Pe}_k} \rightarrow \infty$, both (2.11) and (2.13) can be significantly simplified, and one obtains
${{Pe}_k} \rightarrow \infty$, both (2.11) and (2.13) can be significantly simplified, and one obtains
In the case where ![]() $\bar {p} \rightarrow 1$, and
$\bar {p} \rightarrow 1$, and ![]() $\{\overline {v_s},\bar {\sigma }\} \rightarrow 0$, (2.16) can be further simplified to recover the diffusion-dominated boundary condition (Finneran et al. Reference Finneran, Garner and Nadal2021):
$\{\overline {v_s},\bar {\sigma }\} \rightarrow 0$, (2.16) can be further simplified to recover the diffusion-dominated boundary condition (Finneran et al. Reference Finneran, Garner and Nadal2021):
3. Quasi-steady droplet evaporation
3.1. Solution to the QS problem
In cases where buoyancy is negligible (i.e. large Froude number) and the internal flow in the droplet is absent, the problem becomes spherically symmetric. With further assumptions of a QS incompressible ideal gas phase, negligible pressure work and viscous dissipation (i.e. small Eckert number), constant fluids properties and in the absence of the Soret/Dufour effect and droplet heating, we obtain the following classical formulation of the problem (Spalding Reference Spalding1979; Abramzon & Sirignano Reference Abramzon and Sirignano1989; Finneran et al. Reference Finneran, Garner and Nadal2021):
where ![]() ${\tilde {a}}$ and
${\tilde {a}}$ and ![]() ${\tilde {t}}$ are the rescaled droplet size and time, respectively,
${\tilde {t}}$ are the rescaled droplet size and time, respectively, ![]() ${{Le}}=k_\infty / (c_{p,\infty } \rho _\infty \mathcal {D}_{AB})$ is the Lewis number,
${{Le}}=k_\infty / (c_{p,\infty } \rho _\infty \mathcal {D}_{AB})$ is the Lewis number, ![]() $k$ is the thermal conductivity and
$k$ is the thermal conductivity and ![]() ${\overline {c_p}} = c_{p,\infty }^A/c_{p,\infty }$.
${\overline {c_p}} = c_{p,\infty }^A/c_{p,\infty }$.
Note that both (2.17) and (3.2) are independent of the droplet size ![]() ${\tilde {a}}$ so
${\tilde {a}}$ so ![]() ${{B}_M}$ and
${{B}_M}$ and ![]() ${{B}_T}$ are constants during evaporation under the local thermodynamic assumption (i.e. the limit of
${{B}_T}$ are constants during evaporation under the local thermodynamic assumption (i.e. the limit of ![]() ${{Pe}_k} \rightarrow \infty$), which leads to the classical
${{Pe}_k} \rightarrow \infty$), which leads to the classical ![]() $D^2$-law, i.e.
$D^2$-law, i.e. ![]() ${\tilde {a}}^2 \propto {\tilde {t}}$. However, the
${\tilde {a}}^2 \propto {\tilde {t}}$. However, the ![]() $D^2$-law is no longer valid as we move away from this limit or the surface tension becomes important because both
$D^2$-law is no longer valid as we move away from this limit or the surface tension becomes important because both ![]() ${{B}_M}$ and
${{B}_M}$ and ![]() ${{B}_T}$ will be functions of
${{B}_T}$ will be functions of ![]() ${\tilde {a}}$. As
${\tilde {a}}$. As ![]() ${{Pe}_k}$ reduces, the chemical potential difference across the Knudsen layer increases so the local thermodynamic equilibrium assumption becomes less accurate. As
${{Pe}_k}$ reduces, the chemical potential difference across the Knudsen layer increases so the local thermodynamic equilibrium assumption becomes less accurate. As ![]() ${{Pe}_k}\rightarrow 0$, the mass diffusion of
${{Pe}_k}\rightarrow 0$, the mass diffusion of ![]() $A$ out from the Knudsen layer becomes more efficient than the kinetic process so that the evaporation rate is limited by the slow kinetics. As a result, the out-of-equilibrium kinetics becomes more prominent towards the end of the evaporation process. For a dilute gas,
$A$ out from the Knudsen layer becomes more efficient than the kinetic process so that the evaporation rate is limited by the slow kinetics. As a result, the out-of-equilibrium kinetics becomes more prominent towards the end of the evaporation process. For a dilute gas, ![]() $\mathcal {D}_{AB} \sim T^{3/2}$,
$\mathcal {D}_{AB} \sim T^{3/2}$, ![]() $u_k \sim T^{1/2}$, so
$u_k \sim T^{1/2}$, so ![]() ${{Pe}_k} \sim T^{-1}$ and the local thermodynamic equilibrium can more easily break down at high temperature.
${{Pe}_k} \sim T^{-1}$ and the local thermodynamic equilibrium can more easily break down at high temperature.
The full problem of QS droplet evaporation can be solved numerically based on (3.1) and (3.2), together with the mixed kinetic-diffusion boundary conditions (e.g. (2.11) or (2.13)) and a temperature jump model (e.g. (2.14) or (2.15), or assuming negligible temperature jump). In this work, the numerical results were obtained based on the fourth-order Runge–Kutta methods with variable timesteps to ensure accuracy.
At the slow evaporation limit, the QS droplet evaporation problem based on (3.1), (3.2), (2.13) and (2.14) can be linearised about the equilibrium condition – i.e. ![]() $\{\overline {\delta T},{{B}_M},{{B}_T}\} = 0$ – to get
$\{\overline {\delta T},{{B}_M},{{B}_T}\} = 0$ – to get
where
If (2.15) is used to predict the temperature jump,
The rescaled TED-SRT relation, i.e. (2.11), has a singularity at the equilibrium condition so its linearisation is not pursued in this work.
The solution to problem (3.4) can then be derived as
where
In the large ![]() ${Pe}_0$ limit,
${Pe}_0$ limit, ![]() $c_3$ tends to be zero such that one recovers the classical
$c_3$ tends to be zero such that one recovers the classical ![]() $D^2$-law. At small
$D^2$-law. At small ![]() ${Pe}_0$, the second linear term becomes dominant so the droplet diameter shrinks linearly with time. The solution for the cases of negligible temperature jump across the Knudsen layer can be found by setting
${Pe}_0$, the second linear term becomes dominant so the droplet diameter shrinks linearly with time. The solution for the cases of negligible temperature jump across the Knudsen layer can be found by setting ![]() $s_3^{HK}=0$. The lifetime of the droplet
$s_3^{HK}=0$. The lifetime of the droplet ![]() $\tau _{HK}$ can be found to be
$\tau _{HK}$ can be found to be ![]() $\tau _{HK}=\tau _{D2}(1+ c_3)$, where
$\tau _{HK}=\tau _{D2}(1+ c_3)$, where ![]() $\tau _{D2} = 1/c_4$ is the droplet lifetime assuming local thermodynamic equilibrium. Therefore, the actual lifetime of an evaporating droplet will be longer than the prediction from the classical
$\tau _{D2} = 1/c_4$ is the droplet lifetime assuming local thermodynamic equilibrium. Therefore, the actual lifetime of an evaporating droplet will be longer than the prediction from the classical ![]() $D^2$-law due to the kinetic-limited regime towards the end.
$D^2$-law due to the kinetic-limited regime towards the end.
3.2. Comparison with experimental data
To test the validity of the mixed kinetic-diffusion boundary condition, both the numerical results from the full QS problems and the linearised analytical results are compared with the experimental data reported by Jakubczyk et al. (Reference Jakubczyk, Kolwas, Derkachov, Kolwas and Zientara2012) and Holyst et al. (Reference Holyst, Litniewski, Jakubczyk, Zientara and Woźniak2013b) for the evaporation of triethylene glycol (TEG) and diethylene (DEG) glycol droplets in dry nitrogen and water droplets in humid air. In their experiments, the isolated droplet evaporates very slowly in a nearly isothermal gas domain due to a small gradient in the vapour pressure close to the interface. This enables an accurate time-resolved measurement of the droplet size based on an interferometry technique. Their measurement uncertainty for the droplet size is reported to be up to 10 nm for a single-component droplet (Jakubczyk et al. Reference Jakubczyk, Kolwas, Derkachov, Kolwas and Zientara2012). The physical properties of different fluids and all other parameters used in the model are summarised in table 1. All properties are evaluated from the NIST database (Kroenlein et al. Reference Kroenlein, Muzny, Kazakov, Diky, Chirico, Magee, Abdulagatov and Frenkel2012), except for ![]() $\mathcal {D}_{AB}$ (TEG/DEG in dry nitrogen (Lugg Reference Lugg1968); water in air Massman Reference Massman1998) and
$\mathcal {D}_{AB}$ (TEG/DEG in dry nitrogen (Lugg Reference Lugg1968); water in air Massman Reference Massman1998) and ![]() $p^{\star }$ for TEG and DEG. The saturation pressure
$p^{\star }$ for TEG and DEG. The saturation pressure ![]() $p^{\star }$ at 298 K for both TEG and DEG is very low and no direct experimental data could be found from the literature. Therefore, it was taken as the value leading to the best fit of the measured droplet size, in the region where the classical
$p^{\star }$ at 298 K for both TEG and DEG is very low and no direct experimental data could be found from the literature. Therefore, it was taken as the value leading to the best fit of the measured droplet size, in the region where the classical ![]() $D^2$-law is valid, i.e. when the droplet size is sufficiently large so that the kinetic effects are negligibly small (
$D^2$-law is valid, i.e. when the droplet size is sufficiently large so that the kinetic effects are negligibly small (![]() ${{Pe}_k} > 30$), and the measurement uncertainty is less than 0.5 %.
${{Pe}_k} > 30$), and the measurement uncertainty is less than 0.5 %.
Table 1. Physical properties of fluids used in modelling. Both TEG and DEG are evaporated in dry nitrogen at 298 K, 98.7 kPa. Water is evaporated in humid air at 286 K, 99 kPa and 97 relative humidity. The value of ![]() $\lambda$ in dry nitrogen and humid air is 66 and 63 nm, respectively (Holyst et al. Reference Holyst, Litniewski, Jakubczyk, Zientara and Woźniak2013b).
$\lambda$ in dry nitrogen and humid air is 66 and 63 nm, respectively (Holyst et al. Reference Holyst, Litniewski, Jakubczyk, Zientara and Woźniak2013b).

The predicted ![]() ${\tilde {a}}^2$ and measured
${\tilde {a}}^2$ and measured ![]() ${\tilde {a}}_{{exp}}^2$ and their relative difference, i.e.
${\tilde {a}}_{{exp}}^2$ and their relative difference, i.e. ![]() $({\tilde {a}}_{{exp}}^2-{\tilde {a}}^2)/{\tilde {a}}_{{exp}}^2$, together with the corresponding
$({\tilde {a}}_{{exp}}^2-{\tilde {a}}^2)/{\tilde {a}}_{{exp}}^2$, together with the corresponding ![]() ${{Pe}_k}$ for the evaporation of a water droplet in humid air are shown in figure 2(a,b). We can clearly see that the classical
${{Pe}_k}$ for the evaporation of a water droplet in humid air are shown in figure 2(a,b). We can clearly see that the classical ![]() $D^2$-law (i.e. assuming local thermodynamic equilibrium and ignore surface tension) becomes increasingly inaccurate as the droplet shrinks (i.e.
$D^2$-law (i.e. assuming local thermodynamic equilibrium and ignore surface tension) becomes increasingly inaccurate as the droplet shrinks (i.e. ![]() ${{Pe}_k}$ reduces). At large
${{Pe}_k}$ reduces). At large ![]() ${{Pe}_k}$, the kinetic process is always much more efficient than the mass diffusion so that the evaporation rate is diffusion limited. However, as the kinetic process becomes less efficient than the mass diffusion for reduced droplet sizes, it becomes the limiting factor and the evaporation rate is decreased. When the surface tension is taken into account, the classical model assuming local thermodynamic equilibrium overestimates the evaporation rate even further, due to the increased saturation pressure at small curvature. Incorporating the mixed kinetic-diffusion boundary conditions with no temperature jump across the Knudsen layer can consistently improve the prediction. However, the extent of improvement is dependent on the magnitude of the temperature jump. When the temperature jump is significant, e.g. evaporation of water in humid air – figure 2(a,b), the improvement is very limited. In contrast, when the temperature jump is small, e.g. evaporation of TEG/DEG in dry nitrogen shown in figure 2(c,d), the improvement is very significant. From figure 2, we can also observe that both accommodation coefficients in (1.1) are very close to 1 when the interface is near equilibrium so that negligible differences are introduced by using the semi-empirical HK correlation with unity accommodation coefficients instead of the more rigorous TED-SRT kinetic model. However, the difference will be larger when the evaporation occurs further away from the equilibrium such that there is a larger temperature jump.
${{Pe}_k}$, the kinetic process is always much more efficient than the mass diffusion so that the evaporation rate is diffusion limited. However, as the kinetic process becomes less efficient than the mass diffusion for reduced droplet sizes, it becomes the limiting factor and the evaporation rate is decreased. When the surface tension is taken into account, the classical model assuming local thermodynamic equilibrium overestimates the evaporation rate even further, due to the increased saturation pressure at small curvature. Incorporating the mixed kinetic-diffusion boundary conditions with no temperature jump across the Knudsen layer can consistently improve the prediction. However, the extent of improvement is dependent on the magnitude of the temperature jump. When the temperature jump is significant, e.g. evaporation of water in humid air – figure 2(a,b), the improvement is very limited. In contrast, when the temperature jump is small, e.g. evaporation of TEG/DEG in dry nitrogen shown in figure 2(c,d), the improvement is very significant. From figure 2, we can also observe that both accommodation coefficients in (1.1) are very close to 1 when the interface is near equilibrium so that negligible differences are introduced by using the semi-empirical HK correlation with unity accommodation coefficients instead of the more rigorous TED-SRT kinetic model. However, the difference will be larger when the evaporation occurs further away from the equilibrium such that there is a larger temperature jump.
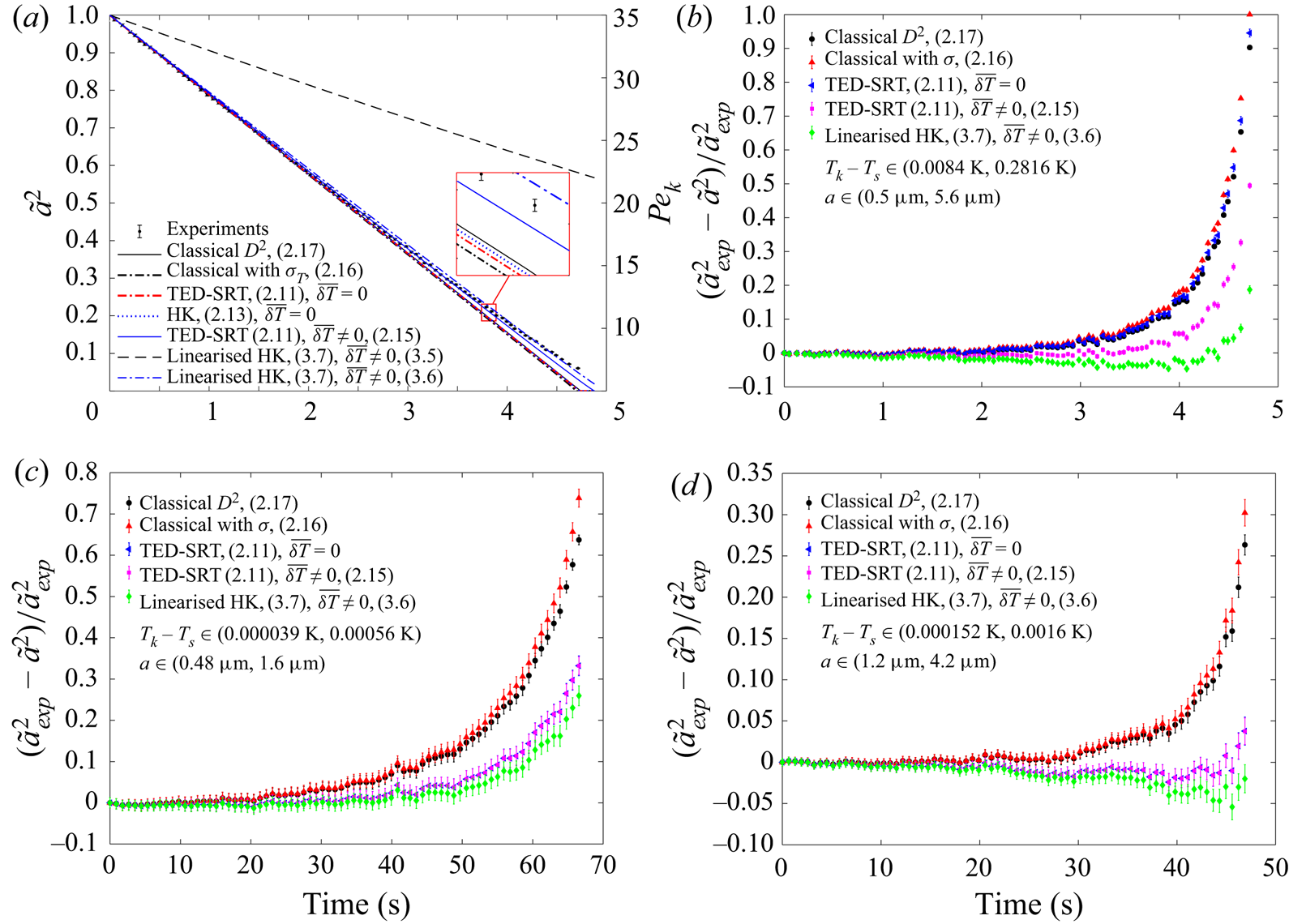
Figure 2. Comparison between the modelled droplet sizes and experimental results. (a,b) Evaporation of a water drop in humid air (experimental data are from Holyst et al. Reference Holyst, Litniewski, Jakubczyk, Zientara and Woźniak2013b). (c) Evaporation of a TEG drop in dry nitrogen (experimental data are from Jakubczyk et al. Reference Jakubczyk, Kolwas, Derkachov, Kolwas and Zientara2012). (d) Evaporation of a DEG drop in dry nitrogen (experimental data are from Holyst et al. Reference Holyst, Litniewski, Jakubczyk, Zientara and Woźniak2013b).
From figure 2(a), we can also see that incorporating the temperature jump model developed for the evaporation of a droplet in its pure vapour (i.e. (2.14)) yields an unrealistically large temperature jump ![]() $\overline {\delta T}$ across the Knudsen layer (
$\overline {\delta T}$ across the Knudsen layer (![]() ${\sim }10\ \mathrm {K}$) and consequentially a significantly slower evaporation rate. A closer look to (2.3) suggests that the large value of
${\sim }10\ \mathrm {K}$) and consequentially a significantly slower evaporation rate. A closer look to (2.3) suggests that the large value of ![]() $\overline {\delta T}$ stems from the very low equilibrium vapour pressure on the liquid surface, i.e.
$\overline {\delta T}$ stems from the very low equilibrium vapour pressure on the liquid surface, i.e. ![]() $p_s^{eq}$ and
$p_s^{eq}$ and ![]() $\overline {\delta T}$ will diverge as
$\overline {\delta T}$ will diverge as ![]() $p_s^{eq} \rightarrow 0$, which is not physically acceptable and needs further correction. If the empirical temperature jump model (2.15) is deployed, the QS solution matches the experimental results well in all cases. This good match is a clear indication of the dominant role that the inert gases play in the thermalisation of the vapour molecules emerging from the evaporation. However, the absence of the physical properties of the pure substance (possibly link to the value of
$p_s^{eq} \rightarrow 0$, which is not physically acceptable and needs further correction. If the empirical temperature jump model (2.15) is deployed, the QS solution matches the experimental results well in all cases. This good match is a clear indication of the dominant role that the inert gases play in the thermalisation of the vapour molecules emerging from the evaporation. However, the absence of the physical properties of the pure substance (possibly link to the value of ![]() $A$) and the heat flux in this empirical correlation means that it does not account for the energy of the emerging vapour molecules properly. The linearised solution, surprisingly, works even better than the full formulation in most cases. This could be an indication that the full formulation needs further revision, possibly through the development of a more rigorous temperature jump model across the Knudsen layer. In summary, among the different models tested, the best option to correct for the error caused by the local thermodynamic equilibrium assumption is to use the mixed kinetic-diffusion boundary condition together with the empirical temperature jump model.
$A$) and the heat flux in this empirical correlation means that it does not account for the energy of the emerging vapour molecules properly. The linearised solution, surprisingly, works even better than the full formulation in most cases. This could be an indication that the full formulation needs further revision, possibly through the development of a more rigorous temperature jump model across the Knudsen layer. In summary, among the different models tested, the best option to correct for the error caused by the local thermodynamic equilibrium assumption is to use the mixed kinetic-diffusion boundary condition together with the empirical temperature jump model.
3.3. Parameter domain study
To quantify the potential errors induced by the local thermodynamic equilibrium assumption on the prediction of the evaporation rate, we compared the values of ![]() ${{B}_T}$ calculated at different
${{B}_T}$ calculated at different ![]() $({{Pe}_k},\varPhi _\infty )$, as shown in figure 3(a). As expected, the error becomes significant when
$({{Pe}_k},\varPhi _\infty )$, as shown in figure 3(a). As expected, the error becomes significant when ![]() ${{Pe}_k} \leqslant O(10)$ and increases as
${{Pe}_k} \leqslant O(10)$ and increases as ![]() ${{Pe}_k}$ is further reduced. Figure 3(b) shows that the errors introduced by neglecting the change in liquid surface chemical potential (due to the presence of inert gas) become significant only when
${{Pe}_k}$ is further reduced. Figure 3(b) shows that the errors introduced by neglecting the change in liquid surface chemical potential (due to the presence of inert gas) become significant only when ![]() $\bar {\rho } \geqslant O(10^{-1})$, which corresponds to high-pressure or low-temperature conditions. Naturally, as one gets closer to the critical point, the ideal gas law breaks down and a more realistic gas model need to be considered.
$\bar {\rho } \geqslant O(10^{-1})$, which corresponds to high-pressure or low-temperature conditions. Naturally, as one gets closer to the critical point, the ideal gas law breaks down and a more realistic gas model need to be considered.

Figure 3. Comparison of ![]() ${{B}_T}$ values calculated at different conditions. Cases of evaporation of a water drop in humid air ignoring the surface tension effect are considered in this calculation:
${{B}_T}$ values calculated at different conditions. Cases of evaporation of a water drop in humid air ignoring the surface tension effect are considered in this calculation: ![]() ${{Le}} = 0.8659$,
${{Le}} = 0.8659$, ![]() $\overline {c_p}=0.6031$,
$\overline {c_p}=0.6031$, ![]() $\bar {p}=0.01$,
$\bar {p}=0.01$, ![]() ${{Ja}}=0.485$,
${{Ja}}=0.485$, ![]() $\gamma =1.124$,
$\gamma =1.124$, ![]() $A = 2.35$,
$A = 2.35$, ![]() $\lambda = 63$ nm. (a) Percentage error coming from the local thermodynamic equilibrium assumption at different
$\lambda = 63$ nm. (a) Percentage error coming from the local thermodynamic equilibrium assumption at different ![]() $\{{{Pe}_k},\varPhi _\infty \}$ when
$\{{{Pe}_k},\varPhi _\infty \}$ when ![]() $\bar {\rho }=1\times 10^{-3}$; (b) percentage error in ignoring the change of liquid phase chemical potential due to the presence of inert gas at different
$\bar {\rho }=1\times 10^{-3}$; (b) percentage error in ignoring the change of liquid phase chemical potential due to the presence of inert gas at different ![]() $\{{{Pe}_k},\bar {\rho }\}$ when
$\{{{Pe}_k},\bar {\rho }\}$ when ![]() $\varPhi _\infty =0.98$.
$\varPhi _\infty =0.98$.
4. Conclusion
In summary, we proposed a more general mixed kinetic-diffusion boundary condition and applied it to solve the QS spherical droplet evaporation problem. The boundary condition formulated here is an extension of the concept of mass conservation across the Knudsen layer introduced by Sultan et al. (Reference Sultan, Boudaoud and Ben Amar2005) and accounts for the Stefan flow due to net evaporation, the change of the chemical potential of the interface due to the presence of inert gases and the temperature jump across the Knudsen layer. The mixed boundary conditions are based on either the semi-empirical HK model or the analytical TED-SRT model developed by Persad & Ward (Reference Persad and Ward2016). The dimensionless forms of the boundary conditions show that the classical ![]() $D^2$-law, i.e.
$D^2$-law, i.e. ![]() $a^2 \propto t$, is valid in the large
$a^2 \propto t$, is valid in the large ![]() ${{Pe}_k}$ limit. In this limit, the kinetics is infinitely fast so that any chemical potential difference across the Knudsen layer is smoothed out and the evaporation rate is limited by the mass diffusion outside the Knudsen layer. As
${{Pe}_k}$ limit. In this limit, the kinetics is infinitely fast so that any chemical potential difference across the Knudsen layer is smoothed out and the evaporation rate is limited by the mass diffusion outside the Knudsen layer. As ![]() ${{Pe}_k}$ reduces, the chemical potential difference across the Knudsen layer starts developing and the local thermodynamic equilibrium assumption breaks down. In the small
${{Pe}_k}$ reduces, the chemical potential difference across the Knudsen layer starts developing and the local thermodynamic equilibrium assumption breaks down. In the small ![]() ${{Pe}_k}$ limit, kinetic processes become the limiting factor and the evaporation rate is significantly lower than that predicted by the classical
${{Pe}_k}$ limit, kinetic processes become the limiting factor and the evaporation rate is significantly lower than that predicted by the classical ![]() $D^2$-law. The linearised solution in the slow evaporation limit produces a linear scaling law, i.e.
$D^2$-law. The linearised solution in the slow evaporation limit produces a linear scaling law, i.e. ![]() $a \propto t$, in the limit of small
$a \propto t$, in the limit of small ![]() ${{Pe}_k}$. Comparison with experimental data available in the literature (Jakubczyk et al. Reference Jakubczyk, Kolwas, Derkachov, Kolwas and Zientara2012; Holyst et al. Reference Holyst, Litniewski, Jakubczyk, Zientara and Woźniak2013b) for the evaporation of TEG, DEG and water droplets suggests that the mixed kinetic-diffusion boundary condition with an empirical temperature jump model (obtained by Holyst et al. (Reference Holyst, Litniewski, Jakubczyk, Zientara and Woźniak2013b) through the curve fitting of data obtained from MD simulations) better predicts the evaporation rate compared with the
${{Pe}_k}$. Comparison with experimental data available in the literature (Jakubczyk et al. Reference Jakubczyk, Kolwas, Derkachov, Kolwas and Zientara2012; Holyst et al. Reference Holyst, Litniewski, Jakubczyk, Zientara and Woźniak2013b) for the evaporation of TEG, DEG and water droplets suggests that the mixed kinetic-diffusion boundary condition with an empirical temperature jump model (obtained by Holyst et al. (Reference Holyst, Litniewski, Jakubczyk, Zientara and Woźniak2013b) through the curve fitting of data obtained from MD simulations) better predicts the evaporation rate compared with the ![]() $D^2$-law, especially in regions where
$D^2$-law, especially in regions where ![]() ${{Pe}_k}\leqslant O(10)$. It has also noted that the existing temperature jump model based on the evaporation of a droplet in its pure vapour proposed by Struchtrup et al. (Reference Struchtrup, Beckmann, Rana and Frezzotti2017) leads to an unrealistic prediction of the temperature jump across the Knudsen layer, at least when the equilibrium vapour pressure is small, and consequentially is a significant underestimation of the evaporation rate. In comparison, the empirical temperature jump model leads to a much better prediction. However, it does not properly account for the energy feed into the vapour molecules emerging from the evaporation (i.e. no dependency on the heat flux). Therefore, a more rigorous temperature jump model needs to be derived that takes into account both the energy feed into the vapour molecules and their thermalisation process due to collisions with the inert gas molecules. At high pressure or low temperature, the increase of the chemical potential at the interface due to the presence of inert gases needs to be accounted for, to better predict the evaporation rate. While the current analysis is limited to the QS evaporation problem, the proposed mixed kinetic-diffusion boundary conditions are applicable to the general problem of droplet evaporation. Accounting for additional effects, such as gas phase transiency, real gas behaviour at high pressure or low temperature and convection both inside and outside droplet, would demand further work.
${{Pe}_k}\leqslant O(10)$. It has also noted that the existing temperature jump model based on the evaporation of a droplet in its pure vapour proposed by Struchtrup et al. (Reference Struchtrup, Beckmann, Rana and Frezzotti2017) leads to an unrealistic prediction of the temperature jump across the Knudsen layer, at least when the equilibrium vapour pressure is small, and consequentially is a significant underestimation of the evaporation rate. In comparison, the empirical temperature jump model leads to a much better prediction. However, it does not properly account for the energy feed into the vapour molecules emerging from the evaporation (i.e. no dependency on the heat flux). Therefore, a more rigorous temperature jump model needs to be derived that takes into account both the energy feed into the vapour molecules and their thermalisation process due to collisions with the inert gas molecules. At high pressure or low temperature, the increase of the chemical potential at the interface due to the presence of inert gases needs to be accounted for, to better predict the evaporation rate. While the current analysis is limited to the QS evaporation problem, the proposed mixed kinetic-diffusion boundary conditions are applicable to the general problem of droplet evaporation. Accounting for additional effects, such as gas phase transiency, real gas behaviour at high pressure or low temperature and convection both inside and outside droplet, would demand further work.
Acknowledgements
We would like to thank Dr D. Jakubczyk for sharing his experimental data and relevant references.
Funding
This research received no specific grant from any funding agency, commercial or not-for-profit sectors.
Declaration of interests
The authors report no conflict of interest.