2.1. Direct numerical simulation

The present computations are performed using the overset DNS method developed by Horne & Mahesh (Reference Horne and Mahesh2019a,Reference Horne and Maheshb). The algorithm is based on the unstructured grid, finite volume method developed by Mahesh, Constantinescu & Moin (Reference Mahesh, Constantinescu and Moin2004) for simulation of the incompressible Navier–Stokes equations. This method emphasizes discrete kinetic energy conservation to ensure robustness at high Reynolds numbers without added numerical dissipation, and has been validated for a variety of complex flows, including free jets (Babu & Mahesh Reference Babu and Mahesh2004) and transverse jets (Muppudi & Mahesh Reference Muppudi and Mahesh2005; Muppidi & Mahesh Reference Muppidi and Mahesh2007; Muppudi & Mahesh Reference Muppudi and Mahesh2008; Sau & Mahesh Reference Sau and Mahesh2010; Iyer & Mahesh Reference Iyer and Mahesh2016). Horne & Mahesh (Reference Horne and Mahesh2019b) extended the method to allow for overset simulation of arbitrarily overlapping and moving meshes. In an overset method, the simulation domain is made up of several overlapping body-fitted meshes, which may be free to move in six-degrees-of-freedom (6DOF) motion. Redundant cells near the boundaries of overlapping meshes are removed, exposing cell faces which require interpolated boundary conditions. The incompressible Navier–Stokes equations are written in an arbitrary Lagrangian-Eulerian (ALE) formulation as

(2.1)$$\begin{gather} \frac{\partial u_i}{\partial t} + \frac{\partial}{\partial x_j} ( u_i u_j - u_i V_j ) ={-} \frac{\partial p}{\partial x_i} + \nu \frac{\partial^2 u_i}{\partial x_j \partial x_j}, \end{gather}$$

(2.2)$$\begin{gather}\frac{\partial u_i}{\partial x_i} = 0, \end{gather}$$

where $u_i$ are the Cartesian velocity components, $p$ is the pressure and $\nu$ is the kinematic viscosity. The mesh velocity, $V_j$, is included in the ALE formulation to avoid tracking multiple reference frames for each mesh, but this term is zero for the present case since there is no mesh motion. The overset method provides several advantages, including simplification of the grid generation process for complex geometries, computational cost savings for high-$Re$ or 6DOF flows and the ability to simulate flow about moving bodies. Issues typical of overset methods are the scaling of the method to large computations and the conservation and interpolation errors at the edges of meshes of differing levels of refinement. The first issue was addressed by the novel parallel communication structure of Horne & Mahesh (Reference Horne and Mahesh2019a) and the second by the interpolation scheme of Horne & Mahesh (Reference Horne and Mahesh2019b). This overset method has been validated for a variety of flows (Horne & Mahesh Reference Horne and Mahesh2019b) and has been applied to successfully perform large-eddy simulation of the turbulent boundary layer over an axisymmetric hull (Morse & Mahesh Reference Morse and Mahesh2021) and a ducted propulsor in crashback (Kroll & Mahesh Reference Kroll and Mahesh2022), as well as DNS of a variety of resolved particle-laden flows (Horne & Mahesh Reference Horne and Mahesh2019b).

The solution is advanced in time using a implicit Crank–Nicolson time stepping with a predictor–corrector scheme, where the velocities are predicted using the momentum equation and subsequently corrected using the pressure Poisson equation to satisfy continuity. Details of the method can be found in Horne & Mahesh (Reference Horne and Mahesh2019b).

2.2. Details of the geometry, grid and computational domain

The flow configuration for the present study consists of a circular jet centred about the origin with a laminar boundary layer cross-flow. A schematic of the problem setup is shown in figure 1, where the origin is selected to be the centre of the jet at the jet exit plane. The $y$ axis points vertically along the nozzle centreline, while the $x$ axis is aligned with the cross-flow direction. The $z$ axis points in the spanwise direction to complete the right-handed coordinate system. The geometry of the nozzle and computational domain sizings are based on those described by Iyer & Mahesh (Reference Iyer and Mahesh2016), who modelled the nozzle shape as a fifth-order polynomial to match the experiments of Megerian et al. (Reference Megerian, Davitian, Alves and Karagozian2007). Jet velocity ratios of $R = 2$ and 4 are chosen with a constant jet Reynolds number of $Re_j = 2000$. In these definitions, $\bar {U}_{{jet}}$ is the mean velocity of the jet assuming a circular exit (ignoring the blockage of the tab). Note that the actual velocity ratios considering the tab blockage are approximately 2.048 and 4.095 for the $R=2$ and $R=4$ cases, respectively.

Figure 1. Computational domain for simulation of the JICF (taken from Regan & Mahesh Reference Regan and Mahesh2019).

The tab in the present computations is a triangular tab with a right-angled apex, matching the dimensions of the tab used in the experiments of Harris et al. (Reference Harris, Besnard and Karagozian2021). A drawing of the jet orifice cross-section with the tab dimensions labelled is shown in figure 2(b). The thickness of the tab is $0.2012D$ and the base width of the tab is $0.25D$, resulting in a 2.3 % geometric blockage of the original circular jet. Note that in the experiments of Harris et al. (Reference Harris, Besnard and Karagozian2021), the nozzle length is extended by $0.19D$ to accommodate the tab template, which slightly weakened the shear layer compared with the original nozzle. We do not incorporate the same extension into the present simulations to permit direct comparisons with the non-tabbed results of Iyer & Mahesh (Reference Iyer and Mahesh2016) and Regan & Mahesh (Reference Regan and Mahesh2017, Reference Regan and Mahesh2019) for the original nozzle.

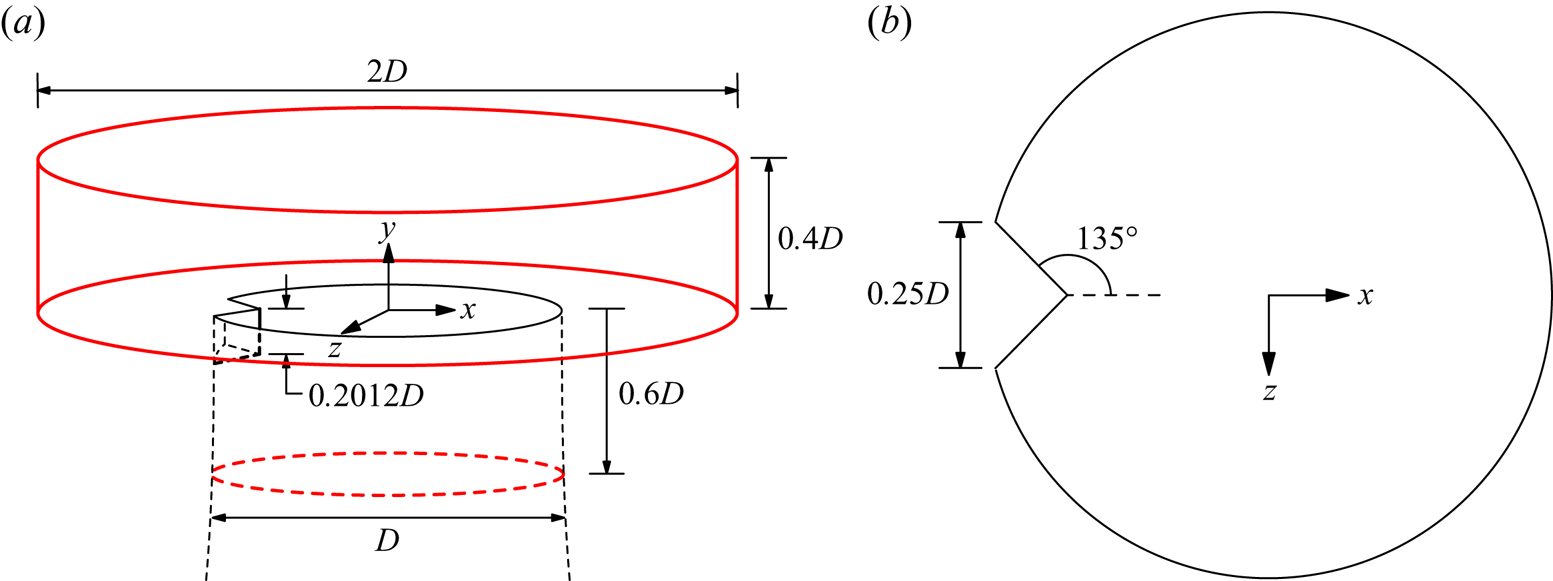
Figure 2. (a) Schematic of the tab overset grid where edges of the grid are shown in red and dimensions are provided for the overset grid boundaries and tab thickness. Panel (b) shows the top view of the upstream tab jet orifice with cross-sectional tab dimensions labelled.

In the computations, the domain is split into two grids: a background grid representing the nozzle, inflow and outflow boundary conditions, and an overset grid for the tab. The background grid does not contain the geometry of the tab and is therefore essentially a replica of the grid that Iyer & Mahesh (Reference Iyer and Mahesh2016) used to study the non-tabbed JICF, although the grid is refined near the jet orifice to interface with the tab grid. The tab grid is shaped as an inverted top-hat shape that fits into the jet exit, and contains wall boundary conditions for the tab, nozzle and cross-flow bottom wall. Figure 2(a) shows the dimensions of the tab overset grid, with the edges of the grid portrayed by red lines. A cylindrical cut is used to remove redundant cells from the background grid, with the grid overlap carefully controlled at interpolation boundaries to target matching cell sizes between the tab and background grids. A slice of the computational mesh around the jet exit and grid overlap for the upstream tab case is shown in figure 3. The split background and tab grid method greatly simplifies the grid generation process and allows the tab grid to be rotated to any angular position around the jet exit, permitting studies of various azimuthal tab locations without requiring creation of new grids. In the present work, two tab orientations are considered:

1. (i) Tab apex pointing in the positive $x$-direction as pictured in figure 2 (corresponding to a tab apex vector of $1 \hat {i} + 0 \hat {k}$); and

2. (ii) tab rotated $45^\circ$ from upstream with the tab apex pointing in the $0.5 \hat {i} - 0.5 \hat {k}$ direction.

These configurations are termed the ‘upstream tab’ and ‘45$^\circ$ tab’, respectively.

Figure 3. Slice of the computational mesh on the centreplane ($z = 0$) for the upstream tab. The overlap between the background and tab grids is visible.

A uniform inflow is provided to the entrance of the jet nozzle, which is located $13.33D$ below the jet exit, as depicted in figure 1. The cross-flow inflow boundary is located at $8D$ upstream of the origin, where a Blasius boundary layer is prescribed. The Blasius inflow profile was chosen to match the laminar boundary layer in the experiments measured with the jet off at a distance $5.5D$ upstream of the jet exit location, as in Iyer & Mahesh (Reference Iyer and Mahesh2016). The resulting momentum thicknesses at the jet exit with the jet turned off are $\theta _{{BL}}/D = 0.1215$ for the $R = 2$ configuration and 0.1718 for $R = 4$. The lateral boundaries are located a distance of $8D$ from the centre of the jet exit, while the top and outflow boundaries are $16D$ from the origin, with these boundaries being assigned zero-gradient Neumann boundary conditions.

Matching the grid sizings of Iyer & Mahesh (Reference Iyer and Mahesh2016), we maintain a spacing of $\Delta x/D = 0.033$ and $\Delta z/D = 0.02$ downstream of the jet exit on the background grid with a minimum $y$-spacing of $\Delta y / D = 0.0013$. There are 400 points distributed around the circumference of the jet exit. The grid spacings near the jet exit are refined in all three coordinate directions compared with Iyer & Mahesh (Reference Iyer and Mahesh2016) to match the resolution of the tab overset grid, which must resolve the flow around the tab. The background grid comprises 163 million cells partitioned over 4048 processors. The tab grid comprises 16.6 million cells partitioned over 440 processors, bringing the total size of the computation to nearly 180 million cells (4488 processors). The computations are advanced implicitly in time with a non-dimensional time step of $\Delta t \bar {U}_{{jet}}/D = 6.7 \times 10^{-4}$.

2.3. Dynamic mode decomposition

Dynamic mode decomposition is a data-driven technique that uses multiple snapshots of observable vectors to identify a set of modes of different frequencies. Originally developed by Rowley et al. (Reference Rowley, Mezić, Bagheri, Schlatter and Henningson2009) and Schmid (Reference Schmid2010), DMD has been used to study JICFs since the method's creation (Rowley et al. Reference Rowley, Mezić, Bagheri, Schlatter and Henningson2009; Chai, Iyer & Mahesh Reference Chai, Iyer and Mahesh2015; Iyer & Mahesh Reference Iyer and Mahesh2016; Schmid Reference Schmid2022). The concept behind DMD is that a set of observable vectors, $\{ \psi _i \}_{i=1}^{N-1}$, obtained as snapshot vectors of flow variables, can be written as a linear combination of DMD modes, $\{ \phi _i \}_{i=1}^{N-1}$, as

(2.3)\begin{equation} \psi_i = \sum_{j=1}^{N-1} c_j \lambda_j^{i-1} \phi_j; \quad i = 1,\ldots,N-1 ,\end{equation}

where $N$ is the number of snapshots, $\lambda _j$ are the eigenvalues of the projected linear mapping and $c_j$ is the $j$th entry of the coefficient vector. The temporal growth/decay rate of a particular mode may be calculated with its corresponding eigenvalue, while the imaginary part of the eigenvalue may be used to calculate the frequency of the mode, $\textrm {Imag}(f_j)$, where $f_j = \ln (\lambda _j)/(2 {\rm \pi}\Delta t)$ and $\Delta t$ is the time spacing between successive snapshots. The spectra of the DMD modes corresponding to the $i$th snapshot vector may then be defined using the set $\{ | c_j \lambda _j^{i-1} | \}_{j=1}^{N-1}$ and the frequency $\textrm {Imag}(f_j)$. In the present work we use the full orthogonalization Arnoldi-based DMD method developed by Anantharamu & Mahesh (Reference Anantharamu and Mahesh2019) for parallel DMD computation of large data sets. For each tabbed jet configuration, $N = 192$ snapshots are saved using a non-dimensional time spacing of $\Delta t \bar {U}_{{jet}}/D = 0.1667$ to produce the DMD results.

3.1. Centreplane

The instantaneous flow fields for the non-tabbed jet, upstream tab and 45$^\circ$ tab at $R = 2$ are shown in figure 4 through contours of $z$-vorticity ($\omega _z$), non-dimensionalized pressure ($p$) and $z$-velocity ($w$) on the centreplane ($z = 0$). Figure 5 shows the same contours for $R = 4$. It is clear from figures 4(b) and 5(b) that the upstream tab displaces the USL in the positive $x$-direction in the centreplane compared with the non-tabbed jet and the jet with the 45$^\circ$ tab (figures 4a,c and 5a,c). Compared with these cases, the contours of $\omega _z$ show that the upstream tab moves the USL vortex pinch-off location further along the shear layer away from the jet exit, suggesting a weakening of the USL instability. This is identical to the behaviour observed by Harris et al. (Reference Harris, Besnard and Karagozian2021), who observed a delay in the USL vorticity roll-up across all velocity ratios for the upstream tab. This weakening is further emphasized by comparison of pressure contours for the three jet configurations in figures 4(d–f) and 5(d–f). For $R = 2$, the differences are the most striking, with the contours of $p$ for the non-tabbed jet and 45$^\circ$ tab (figure 4d–f) showing much lower pressures in the USL vortex cores than for the upstream tab (figure 4e). For $R = 4$, the USL vortex core pressures are similar between the upstream tab and other configurations. However, for the non-tabbed jet and 45$^\circ$ tab at $R = 2$, contours of $\omega _z$ show larger, more circular vortex cores in the USL that persist further down the shear layer than the USL vortices for the upstream tab, which are smaller and more distorted. This is especially apparent for the 45$^\circ$ tab. The opposite phenomenon is observed for $R = 4$, where the USL vortices for the 45$^\circ$ tab are much more greatly distorted in the centreplane than the nearly circular vortices for the upstream tab. The non-tabbed jet for $R = 4$ shows strong pairing of vortices between the USL and DSL, as the snapshot is taken during the vortex merging process.

Figure 4. Instantaneous contours of $\omega _z D/\bar {U}_{{jet}}$ (a–c), $p/\rho \bar {U}_{{jet}}^2$ (d–f) and $w/\bar {U}_{{jet}}$ (h–j) on the centreplane ($z = 0$) of the jet at $R = 2$. Results for the non-tabbed jet of Iyer & Mahesh (Reference Iyer and Mahesh2016) (a,d,g), upstream tab (b,e,h) and the 45$^\circ$ tab (c, f,i) are shown.

Figure 5. Instantaneous contours of $\omega _z D/\bar {U}_{{jet}}$ (a–c), $p/\rho \bar {U}_{{jet}}^2$ (d–f) and $w/\bar {U}_{{jet}}$ (h–j) on the centreplane ($z = 0$) of the jet at $R = 4$. Results for the non-tabbed jet of Iyer & Mahesh (Reference Iyer and Mahesh2016) (a,d,g), upstream tab (b,e,h) and the 45$^\circ$ tab (c, f,i) are shown.

Further differences between the upstream tab and other configurations are made apparent from contours of spanwise velocity ($w$) in figures 4(g–i) and 5(g–i). Considering the jet at $R = 2$, we observe only minor differences between the three configurations. The jet's potential core and the centre of the USL vortices for the 45$^\circ$ tab show a slight negative $z$-velocity. Note that since the 45$^\circ$ tab is placed on the $z>0$ side of the nozzle, a negative $z$-velocity corresponds to flow away from the side of the nozzle with the tab. Contours of $w$ in the potential core for the upstream tab and non-tabbed jet show no preferential sign and the instantaneous wake behind the jet exit appears relatively similar between the two tab configurations. In contrast, there are stark differences in $w$ between the upstream and 45$^\circ$ tabs for $R = 4$. The most striking flow feature of the 45$^\circ$ tab are the bands of strong positive and negative $w$ in the wake behind the jet. The upstream tab, on the other hand, shows weaker fluctuations of $w$ in the wake in response to upright wake vortices, as identified for round JICFs by Fric & Roshko (Reference Fric and Roshko1994). Interestingly, these wake fluctuations are stronger than for the non-tabbed jet. In addition, the potential core and the USL vortices for the 45$^\circ$ tab at $R = 4$ show even stronger negative $w$ than was observed for the 45$^\circ$ tab at $R = 2$, indicating a stronger deflection of the USL in the negative $z$-direction.

3.2. The USL spectra

Figure 6(a,b) shows USL spectra for $R = 2$ at locations $s/D = 0.1, 1, 2, 3, 4, 5$ along the USL for the upstream and 45$^\circ$ tabs. For comparison, figure 7 shows the spectra reported by Iyer & Mahesh (Reference Iyer and Mahesh2016) for the non-tabbed jet at $R = 2$ and 4. Note that amplitudes of these spectra differ from the present results due to minor differences in the way the spectra were extracted. The Strouhal number ($St = fD/\bar {U}_{{jet}}$) corresponding to the dominant shear layer frequency is $St_0 = 0.87$ for the upstream tab and $St_0 = 0.73$ for the 45$^\circ$ tab, compared with 0.76 for the non-tabbed jet of Iyer & Mahesh (Reference Iyer and Mahesh2016). The increase of the dominant USL frequency over the non-tabbed configuration is similar to that observed in the experimental spectra of Harris et al. (Reference Harris, Besnard and Karagozian2021). For both tabs, the spectra show signatures of the USL instability beginning at $s/D = 0.1$, although the instability is stronger for the 45$^\circ$ tab, and for both cases the instability appears less developed than that of the non-tabbed jet at the same location (figure 7a). Interestingly, a subharmonic peak at $St \approx 0.35$ forms at this location for the upstream tab, which is similar to the subharmonic peak at $St = 0.32$ reported by Harris et al. (Reference Harris, Besnard and Karagozian2021) for the same tab configuration at $J = 7$. Moving along the USL, the sharp spectral peaks for the 45$^\circ$ tab persist in the shear layer all the way to $s/D \geq 5$. In contrast, the dominant peak for the upstream tab diminishes into a broadband spectrum by $s/D \approx 4$, as the spanwise USL structures are quickly broken up into turbulence. This echoes the stronger coherence of the USL vortices observed in figure 4(c) compared with figure 4(b). Figure 6(c,d) shows corresponding spectra of the non-dimensional drag fluctuations on the tab, which show signatures of the dominant USL frequency and its harmonics, despite their low magnitude. This suggests that the oscillating forces on the tab are related to feedback from the USL rather than shedding from the tab.

Figure 6. The USL spectra of fluctuating $y$-velocity at locations $s/D = 0.1, 1, 2, 3, 4, 5$ (shown in warm to cool colours) for the upstream tab (a) and the 45$^\circ$ tab (b) at $R = 2$. The dominant shear layer Strouhal number is labelled. Corresponding spectra of the non-dimensional fluctuating tab drag, $F_y'/\bar {F}_y$, for each case are shown in panels (c) and (d).

Figure 7. The USL spectra of fluctuating $y$-velocity from Iyer & Mahesh (Reference Iyer and Mahesh2016) shown with warm to cool colours for locations $s/D = 0.1, 1, 2, 3$ for $R = 2$ (a) and $s/D = 0.1, 1, 2, 3, 4, 5$ for $R = 4$ (b). The dominant shear layer Strouhal number is labelled.

Figure 8 shows similar spectra for the $R = 4$ jet with the upstream and 45$^\circ$ tab. Comparing the spectra for these two tabs and the non-tabbed spectra from Iyer & Mahesh (Reference Iyer and Mahesh2016) (figure 7b) demonstrates the remarkable reduction in the strength of the shear layer instability for the upstream tab. The jet with the upstream tab shows much broader spectral double peaks and a dramatic reduction in the power of the harmonics of the dominant frequency. A similar effect can be observed in the spectral contour maps of Harris et al. (Reference Harris, Besnard and Karagozian2021) for an upstream tab at $J = 61$ and $Re_j = 2300$. Note that in contrast to Harris et al. (Reference Harris, Besnard and Karagozian2021), the DNS does not display frequency shifting along the USL, since experimental shear layer frequency shifting can be attributed to tonal interference between the probe and the instability frequency, as noted in Hussain & Zaman (Reference Hussain and Zaman1978) and Harris et al. (Reference Harris, Besnard and Karagozian2021). Interestingly, the strong subharmonic peak for the non-tabbed jet at $R = 4$ is eliminated until later along the USL, where vortex merging takes place. The Strouhal number corresponding to the dominant shear layer frequency is $St_0 = 0.78$ for the upstream tab vs $St_0 = 0.82$ for the 45$^\circ$ tab and 0.92 for the non-tabbed jet. Interestingly, for $R = 4$, the 45$^\circ$ tab produces an increase in the $St_0$ over the value for the upstream tab, while the opposite is true for $R = 2$.

Figure 8. The USL spectra of fluctuating $y$-velocity at locations $s/D = 0.1, 1, 2, 3, 4, 5$ (shown in warm to cool colours) for the upstream tab (a) and the 45$^\circ$ tab (b) at $R = 4$. The dominant shear layer Strouhal number is labelled. Corresponding spectra of the non-dimensional fluctuating tab drag, $F_y'/\bar {F}_y$, for each case are shown in panels (c) and (d).

Again, the spectra of the fluctuating drag force on the tab are plotted in figure 8(c,d). In contrast to the same plots for $R = 2$ (figure 6c,d), the magnitude of the force spectra is far lower and there is not an obvious signature of the dominant shear layer frequencies from the velocity spectra. While there is a peak in the force spectra for the upstream tab corresponding to $St_0$ (figure 8c), it is near the spectral floor. The spectra for the 45$^\circ$ tab (figure 8d) shows no signature of a peak relating to the dominant USL frequency. This result demonstrates that the tab does not shed at a specific frequency to influence the shear layer development, but instead influences the USL through a stable modification of the shear layer issuing out of the jet. These results also indicate that the signatures of the dominant USL frequencies in the tab force spectra at $R = 2$ are due to the proximity of the shear layer roll-up to the tab. The feedback from the shear layer produces periodic oscillations of the flow field around the tab, thus altering the tab forces.

8.1. Jet centreplane and USL/DSL

Figure 21 shows centreplane contours of turbulent kinetic energy, $k = \frac {1}{2} \overline {u'_i u'_i}$, variance of pressure fluctuations, $\overline {p'^2}$, and spanwise unsteadiness, $\overline {w'^2}$, for the non-tabbed jet (Regan & Mahesh Reference Regan and Mahesh2019), upstream tab and 45$^\circ$ tab at $R = 2$. Also shown are centreplane streamlines originating from the centre, upstream and downstream sides of the jet (———) and a contour line marking $\bar {u}=0$ (– – – – –) to indicate the recirculation region behind the jet column. Additional statistics for mean spanwise vorticity, pressure, $x$-velocity, and $y$-velocity can be found in the supplementary material for a full comparison with Iyer & Mahesh (Reference Iyer and Mahesh2016). As was observed from the instantaneous contours in figure 4, the contours of $k$ and $\overline {p'^2}$ show that the USL instability is delayed and significantly weakened by the upstream tab. This is especially apparent from the contours of $\overline {p'^2}$, which provide a better measure of the shear layer vortex strengths due to the local pressure minima at the centre of larger, more coherent vortices. Examination of the $\overline {p'^2}$ plot for the upstream tab (figure 21e) reveals that the DSL is also weakened with the upstream tab. Interestingly, the growth of $k$ and $\overline {p'^2}$ in the DSL appear in the region between the DSL streamline and the recirculation region, which is similar to the location of the wavemaker predicted by Ilak et al. (Reference Ilak, Schlatter, Bagheri and Henningson2012) for the primary instability of the JICF at low $R$. Comparing the plots of $k$, it also appears that the presence of the upstream tab slightly reduces the jet penetration. Figure 21(g–i) shows the spanwise unsteadiness for the $R = 2$ jet, the maximum of which is located directly downstream of the nozzle, as in the non-tabbed configuration (Iyer & Mahesh Reference Iyer and Mahesh2016). The remainder of $\overline {w'^2}$ resides in the DSL, and relatively little spanwise unsteadiness is observed in the USL, even for the upstream tab, presumably due to the symmetric nature of the streamwise $\varLambda$-shaped vortices. However, spanwise unsteadiness begins to emerge for this case as the USL and DSL meet (figure 21h), suggesting the influence of the DSL in breaking the symmetry of the streamwise vortex structures from the upstream tab. Figure 21(i) shows that the 45$^\circ$ tab significantly reduces the peak in spanwise unsteadiness behind the jet column just above the jet exit, despite similar values of $k$ as the other jet configurations.

Figure 21. Contours of $k$ (a–c), $\overline {p'^2}$ (d–f) and $\overline {w'^2}$ (g–i) normalized by $\rho$ and $\bar {U}_{{jet}}$ on the centreplane for $R = 2$. Mean streamlines from the upstream edge, centre and downstream edge of the nozzle are shown as solid black lines and the contour line for $\bar {u} = 0$ (– – – – –) is shown to mark recirculation zones. Results are shown for the non-tabbed jet from Regan & Mahesh (Reference Regan and Mahesh2019) (a,d,g), the upstream tab (b,e,h) and the 45$^\circ$ tab (c, f,$i$).

Similarly, figure 22 shows contours of $k$, $\overline {p'^2}$ and $\overline {w'^2}$ for the non-tabbed jet, upstream tab and 45$^\circ$ tab at $R = 4$. From the contours of $\overline {p'^2}$, it is clear how much the upstream tab delays the roll-up of the USL vortices, as observed by Harris et al. (Reference Harris, Besnard and Karagozian2021). Even though contours of $k$ for the 45$^\circ$ tab show higher levels of unsteadiness in the shear layer compared with the non-tabbed jet, the contours of $\overline {p'^2}$ indicate that the USL instability is delayed and weakened, albeit not as much as for the upstream tab. This difference likely relates to the observations from figures 5(c) and 16(b), where the spanwise vortices in the USL were split into helical vortices, resulting in weaker vortex cores but a large level of unsteadiness. The contours of $k$ and $\overline {p'^2}$ also indicate a delay of the DSL instability for the upstream and 45$^\circ$ tabs. Again, the location of the peaks of $k$ and $\overline {p'^2}$ between the recirculation region and the DSL is quite similar to the wavemaker location predicted by Ilak et al. (Reference Ilak, Schlatter, Bagheri and Henningson2012) for the onset of the JICF instability at lower $R$. In a similar manner to the $R = 2$ jet, the upstream tab produces a stronger peak in the $\overline {w'^2}$ where the USL and DSL meet than for the non-tabbed case. The high values of $\overline {w'^2}$ for the 45$^\circ$ tab in the USL and DSL can be attributed to the skewing of the jet away from the tab.

Figure 22. Contours of $k$ (a–c), $\overline {p'^2}$ (d–f) and $\overline {w'^2}$ (g–i) normalized by $\rho$ and $\bar {U}_{{jet}}$ on the centreplane for $R = 4$. Mean streamlines from the upstream edge, centre and downstream edge of the nozzle are shown as solid black lines and the contour line for $\bar {u} = 0$ (– – – – –) is shown to mark recirculation zones. Results are shown for the non-tabbed jet from Regan & Mahesh (Reference Regan and Mahesh2019) (a,d,g), the upstream tab (b,e,h) and the 45$^\circ$ tab (c, f,i).

To further investigate the development of unsteadiness in the USL, figure 23 plots $k$ and spanwise unsteadiness ($\overline {w'^2}$) vs distance $s$ along the shear layer. The $s$ coordinate and corresponding profiles were extracted from the centreplane streamline originating at the upstream side of the nozzle at the jet exit plane, as visible in figures 21 and 22. This streamline was found to follow a similar profile as the location of maximum vorticity in the USL, as may be verified in the supplementary material. Figure 23(a) shows the development of $k$ along the shear layer for the non-tabbed jet, the upstream tab, and the 45$^\circ$ tab at $R = 2$. While the 45$^\circ$ tab and non-tabbed jet show a nearly identical rise of $k$ downstream of the jet exit, the upstream tab exhibits a slight delay before this increase, suggesting a delay of the USL instability. The initial peak of $k$ is also much lower for the upstream tab and non-tabbed jets, confirming that the USL instability is weaker in this case. In contrast, the second peak in $k$ is of similar magnitude for the non-tabbed jet and the upstream tab, while the 45$^\circ$ tab produces a higher peak. The location of this peak aligns with the meeting of the USL and DSL where the potential core of the jet closes. We can see that this peak is nearly in the same location for the non-tabbed jet and the 45$^\circ$ tab, but occurs earlier for the upstream tab, due to the closer proximity of the USL and DSL in the centreplane.

Figure 23. Profiles of $k$ (a,b) and $\overline {w'^2}$ (c,d) for $R = 2$ (a,c) and $R = 4$ (b,d). Profiles were extracted from a streamline originating at the upstream edge of the jet exit on the jet exit plane (note that the streamline for the upstream tab originates from the tab apex). Results for the non-tabbed jet of Regan & Mahesh (Reference Regan and Mahesh2019) ($\cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot$), the upstream tab (———) and the 45$^\circ$ tab (– – – – –) are shown.

Looking at the development of $\overline {w'^2}$ in figure 23(c), the 45$^\circ$ tab produces a peak at $s/D \approx 1$, which occurs after the rise in $k$ but is earlier than the development of $\overline {w'^2}$ for the upstream tab and the non-tabbed jet. This relates to the observations from figure 4(i), where the 45$^\circ$ tab showed a negative $w$ in the jet potential core and in the cores of the USL vortices. The non-tabbed jet shows a peak in $\overline {w'^2}$ at $s/D \approx 1.6$, but this development of spanwise unsteadiness is delayed and much weaker than either of the tabbed configurations, until the second peak in $\overline {w'^2}$, where the USL and DSL meet. While the upstream tab does not produce as rapid of a rise in $\overline {w'^2}$ as the 45$^\circ$ tab, it does rise slowly from $s/D \approx 0.8$ to $s/D = 3$, maintaining a high level of spanwise unsteadiness in the USL. This unsteadiness only appears after the initial peak in $k$ and is likely related to the development of streamwise vortices in the USL following the spanwise instability. By $s/D = 4$, the other jet configurations have overtaken the $\overline {w'^2}$ of the upstream tab due to the comparatively delayed merging of the USL and DSL.

Considering the jets at $R = 4$, figure 23(b) shows a delay in the development of the USL instability for both tabbed jets. In contrast to the results for $R = 2$, the 45$^\circ$ tab produces a substantial delay in the onset of the USL instability, and the upstream tab produces an even further delay, corresponding to the observations of USL vortex roll-up in figure 5. In terms of spanwise unsteadiness, the 45$^\circ$ tab produces much larger values of $\overline {w'^2}$ than either the upstream tab or the non-tabbed jet with a peak that is over double any of the peaks of $\overline {w'^2}$ for $R = 2$. This is striking given the observation that $\overline {w'^2}$ in the USL is much higher at lower $R$ for non-tabbed jets (Iyer & Mahesh Reference Iyer and Mahesh2016). The source of this large peak in spanwise unsteadiness relates to the negative $w$ observed in the cores of USL vortices in figure 5(i) due to the skewing of the jet shear layer away from the tabbed side of the jet. In contrast to $R = 2$, this elevated value of $\overline {w'^2}$ for the 45$^\circ$ tab remains above that of the other configurations all the way to $s/D > 6$, which is indicative of the greater asymmetry of the jet at $R = 4$.

Given the interaction between the tab and the DSL, as discussed in § 6, figure 24 plots the development of $k$ and $\overline {w'^2}$ along the DSL for each jet configuration. In a similar manner as the USL analysis, the $s$ coordinate and corresponding profiles were extracted from the centreplane streamline originating at the downstream side of the nozzle ($x = 0.5D$, $y = 0$), as visible in figures 21 and 22. For $R = 2$, the peak value of $k$ and subsequent decay for $s/D > 2$ are similar between the different tab configurations, although for the 45$^\circ$ tab, the rate of increase of $k$ above the jet exit is reduced. Examining the evolution of $\overline {w'^2}$ in figure 24(c), we find that compared with the non-tabbed jet, the initial peak is reduced for the upstream tab and nearly eliminated for the 45$^\circ$ tab, possibly due to the asymmetry induced by this tab configuration.

Figure 24. Profiles of $k$ (a,b) and $\overline {w'^2}$ (c,d) for $R = 2$ (a,c) and $R = 4$ (b,d). Profiles were extracted from a streamline originating at the downstream edge of the jet exit on the jet exit plane. Results for the non-tabbed jet of Regan & Mahesh (Reference Regan and Mahesh2019) ($\cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot$), the upstream tab (———) and the 45$^\circ$ tab (– – – – –) are shown.

For the jet at $R = 4$, the evolution of $k$ (figure 24b) suggests that the onset of the DSL roll-up occurs at $s/D \approx 0.8$, which is similar between the different tab configurations. However, $k$ rises much more rapidly for the non-tabbed jet, although it reaches its peak further along the shear layer than the peak for the tabbed jets. The tab does not have a notable impact on the peak value of $k$. However, from the evolution of $\overline {w'^2}$ (figure 24(d), we see that there is a much higher peak for the 45$^\circ$ tab compared with the upstream and non-tabbed jet configurations. This is likely due to the skewing of the CVP into the centreplane, on which the streamline is extracted.

8.2. Jet penetration and cross-section

Figure 25 shows cross-sectional slices of the CVP at $x/D = 4$ coloured by average $x$-vorticity ($\bar {\omega }_x$). The non-tabbed jets and the upstream tab show symmetry of the CVP at both $R = 2$ and $R = 4$. The effect of the upstream tab is to flatten the jet cross-section and reduce the jet penetration, as observed by Harris et al. (Reference Harris, Besnard and Karagozian2021). Interestingly, this effect is most pronounced at $R = 4$, where the CVP is significantly widened and flattened, producing much larger lateral spreading of the CVP. This has been observed experimentally under similar conditions (Zaman Reference Zaman1998; Bunyajitradulya & Sathapornnanon Reference Bunyajitradulya and Sathapornnanon2005; Harris et al. Reference Harris, Besnard and Karagozian2021), although this effect was relatively obscured by the asymmetric CVP in Bunyajitradulya & Sathapornnanon (Reference Bunyajitradulya and Sathapornnanon2005) and Harris et al. (Reference Harris, Besnard and Karagozian2021) due to the sensitivity of the JICF to asymmetric experimental disturbances.

Figure 25. Contours of $\bar {\omega }_x D/\bar {U}_{{jet}}$ on a slice at $x/D = 4$ for $R = 2$ (a–c) and $R = 4$ (d–f). Results are shown for the non-tabbed jet from Regan & Mahesh (Reference Regan and Mahesh2019) (a,d), the upstream tab (b,e) and the 45$^\circ$ tab (c, f).

The 45$^\circ$ tab produces a much starker contrast between its effect on the jet at $R = 4$ compared with $R = 2$. At $R = 2$, the 45$^\circ$ tab only produces a very slight asymmetry of the CVP and the cross-section appears quite similar to the non-tabbed case. Conversely, the 45$^\circ$ tab at $R = 4$ produces a large deflection of the CVP in the negative $z$-direction away from the side of the jet with the tab. The tertiary vortex that was observed in figure 16(b) is also visible below the CVP (labelled in figure 25f) and has a similar vorticity magnitude as the CVP. The mean flow associated with this vortex structure will be discussed more in depth in § 8.4.

Despite the smaller visual asymmetries described for the 45$^\circ$ tab at $R = 2$, contours of mean spanwise velocity in figure 26(a) show that the asymmetry due to the tab does induce a significant mean spanwise velocity behind the jet. In fact, this velocity is of similar magnitude as the mean spanwise velocity for the 45$^\circ$ tab at $R = 4$ (figure 26b). Note that the mean spanwise velocity for the symmetric jet configurations (upstream tab and non-tabbed jets) averages to zero on the symmetry plane. While the bands of mean spanwise velocity for $R = 4$ in figure 26(b) appear very similar to the contours of instantaneous $w$ in figure 5(i), the symmetry breaking of the 45$^\circ$ tab for $R = 2$ was obscured in figure 4(i) due to the unsteadiness in the wake of the jet. Of particular note for the 45$^\circ$ tab at $R = 2$ is the strong positive spanwise velocity directly behind the jet core, which may relate to the lower levels of spanwise unsteadiness behind the jet observed for this configuration (figure 21i).

Figure 26. Contours of $\bar {w}$ normalized by $\bar {U}_{{jet}}$ on the centreplane for $R = 2$ (a) and $R = 4$ (b) for the 45$^\circ$ tab. The mean spanwise velocity for the symmetric jet configurations (non-tabbed jet and upstream tab) averages to zero on the symmetry plane. Mean streamlines from the upstream edge, centre and downstream edge of the nozzle are shown as solid black lines and the contour line for $\bar {u} = 0$ (– – – – –) is shown to mark recirculation zones.

Figure 27(a) shows the trajectory of the three-dimensional jet centre streamline for the upstream tab, 45$^\circ$ tab and non-tabbed jet (Regan & Mahesh Reference Regan and Mahesh2019) at $R = 2$ and $R = 4$, while figure 27(b) compares the penetration of the tabbed jets vs the non-tabbed jet at the same $R$. First, we observe a reduction in jet penetration for the upstream tab compared with the non-tabbed case of Iyer & Mahesh (Reference Iyer and Mahesh2016) at both velocity ratios, as noted in several experimental studies (Liscinsky et al. Reference Liscinsky, True and Holdeman1995; Zaman & Foss Reference Zaman and Foss1997; Bunyajitradulya & Sathapornnanon Reference Bunyajitradulya and Sathapornnanon2005; Harris et al. Reference Harris, Besnard and Karagozian2021). Additionally, from figure 27(b), we can observe that the upstream tab for the $R = 4$ jet produces a larger reduction in penetration than is observed for the same tab at $R = 2$. This is consistent with the experimental observations of Zaman (Reference Zaman1998), who found a more dramatic reduction in jet penetration due to the tab at higher $J$. While the upstream tab produces a fairly uniform reduction in jet penetration along $x$, the 45$^\circ$ tab produces a different behaviour. For $R = 2$, the 45$^\circ$ tab actually increases the penetration of the centre streamline compared with the non-tabbed jet until $x \approx 8.5D$, after which the relative penetration is reduced. For $R = 4$, the 45$^\circ$ tab produces a small reduction in the centre streamline penetration near the jet exit, which increases nearly linearly after $x \approx 2.5D$. This behaviour is presumably due to the skewing of the CVP cross-section induced by the 45$^\circ$ tab at this $R$ (figure 25f), which suppresses the jet penetration due to redirection of the induced flow from the CVP.

Figure 27. Jet trajectory along the centre streamline originating from $(x,y,z) = (0,0,0)$ (a) and difference in jet penetration vs the non-tabbed jet of Regan & Mahesh (Reference Regan and Mahesh2019) (b). Accompanying profiles of velocity magnitude (c,d) and turbulent kinetic energy (e, f) are plotted along the centre streamline vs distance from the jet exit, $s$. Results for the upstream tab (———), 45$^\circ$ tab (– – – – –) and the non-tabbed jet from Regan & Mahesh (Reference Regan and Mahesh2019) ($\cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot$) are shown, with results for $R = 2$ appearing in blue and results for $R = 4$ appearing in red. A slope of $-$1 is plotted in panel (d), corresponding to the classic turbulent round jet centreline velocity decay, while a slope of $-1.83$ is plotted in panel ( f), corresponding to the value from similarity analysis of Sadeghi et al. (Reference Sadeghi, Lavoie and Pollard2015) for the decay of centreline turbulent kinetic energy of finite-$Re_j$ regular jets.

Figure 27(c,d) shows the development of the mean streamwise velocity ($U_s$) for each jet vs the streamwise distance $s$ along the centre streamline. The beginning of the centre streamline velocity decay is delayed for $R = 4$ compared with $R = 2$ and the 45$^\circ$ tab induces a further delay in both jets. The decay of $U_s$ for each jet approximately follows the $-1$ power law expected for regular jets, although some tab configurations show a greater rate of decay. Figure 27(e, f) shows the decay of turbulent kinetic energy vs $s$ along the centre streamline. For both $R = 2$ and $R = 4$, the upstream tab moves the peak of $k$ closer to the jet exit due to the more rapid closing of the jet potential core, whereas the 45$^\circ$ tab moves it farther from the jet exit compared with the non-tabbed jet. This effect is more pronounced at $R = 4$, where we also note that the peak value of $k$ is reduced for the 45$^\circ$ tab. Following the peak in $k$, the turbulent kinetic energy decays according to a power law relationship. Figure 27( f) plots a line corresponding to the $-1.83$ power law found by Sadeghi, Lavoie & Pollard (Reference Sadeghi, Lavoie and Pollard2015) from similarity analysis of regular jets. The $R = 2$ jets show a slightly lower decay than this value, except for the 45$^\circ$ tab, which exhibits a slightly higher decay rate than the other configurations. The $R = 4$ jets all experience a larger decay of $k$ than regular jets, with the 45$^\circ$ tab again producing the largest rate of decay.

8.3. Flow inside the jet nozzle

Given the conclusions from time history and spectra that the effect of the tab is to produce a disturbance in the mean flow, it follows to assess how the presence of the tab affects the jet flow out of the nozzle, with particular focus on the USL. Figure 28 shows mean surface streamlines inside of the nozzle just below the jet exit plane ($y = 0$) on an unwrapped surface of the nozzle. The azimuthal coordinate is defined as $\phi = \textrm {arctan}(-z/x)$ such that $\phi = 0$ is the upstream side of the nozzle.

Figure 28. Surface streamlines on the nozzle and tab surfaces for the upstream tab at $R = 2$ (a) and $R = 4$ (b) and the 45$^\circ$ tab at $R = 2$ (c) and $R = 4$ (d). Note that the azimuthal coordinate is defined as $\phi = \textrm {arctan}(-z/x)$ such that $\phi = 0^\circ$ corresponds to the upstream side of the nozzle.

Figure 28(a,b) shows these streamlines for the upstream tab at $R = 2$ and 4, respectively. The boundary layer in the jet nozzle stagnates in front of the tab, producing a saddle point below the tab with an accompanying separation line and junction vortex system. Kelso & Smits (Reference Kelso and Smits1995) detailed the flow topology of a round (non-tabbed) JICF and identified the separation inside the nozzle, consisting of a negative bifurcation (separation) line and a saddle point and node at $\phi = 0^\circ$, where the node lies at the jet exit. The size of the separation envelope was found to decrease with increasing $R$, with an accompanying shift of the saddle point towards the top of the nozzle until $R > 6$, where the saddle point coincided with the lip of the nozzle. This shift has also been observed in jet simulations (Muppudi & Mahesh Reference Muppudi and Mahesh2005) and is attributed to the higher adverse pressure gradient on the upstream side of the nozzle at low $R$ due to the increased stagnation pressure of the cross-flow. For the case of the tabbed jet, the node is shifted to the stagnation point below the bottom surface of the tab for both $R = 2$ and $R = 4$, and the saddle point on the separation line is located only slightly lower for $R = 2$ than for $R = 4$. The fact that the saddle point and initiation of separation are at similar locations for the tabbed jet is intuitive as the adverse pressure gradient imposed by the stagnation point on the tab dominates the effect of the cross-flow stagnation. However, the separation line issuing from the saddle point shows significant differences based on $R$ as it spreads around the tab. Examining the streamline patterns for the upstream tab, the separation envelope for $R = 2$ spreads much more laterally than for $R = 4$, since the flow passing around the tab feels a stronger adverse pressure gradient in the $y$-direction at lower $R$. Additionally, surface streamlines near the jet exit for $R = 2$ show that the cross-flow penetrates into the nozzle to nearly half the height of the tab. In contrast, for $R = 4$ there is almost no penetration of the cross-flow into the nozzle.

For the 45$^\circ$ tab (figure 28c,d), the same observations may be made about the location of the node and saddle point for $R = 2$ and 4. However, in this case the adverse pressure gradient due to the cross-flow stagnation leads to differences in the skewing of the streamlines around the tab. For $R = 2$, the separation line near the front of the nozzle curls back towards the tab surface, and the downstream separation line extends laterally past $\phi = 90^\circ$ by the jet exit. Additionally, streamlines near the upstream side of the nozzle ($\phi = 0^\circ$) splay in the positive and negative $\phi$-directions on each side of $\phi = 0^\circ$ due to the adverse pressure gradient arising from the cross-flow. For $R = 4$, the separation line looks far more similar to the streamline patterns for the upstream tab (figure 28b) as the upstream and downstream separation lines are only slightly deflected in the positive $\phi$-direction by the cross-flow. As a result, the separation envelope due to the tab for $R = 4$ has a much greater influence on the trajectory of the streamlines near $\phi = 0^\circ$, which skew towards the negative $z$-direction at the jet exit. This explains why the USL and jet cross-section at $R = 4$ skew much more strongly away from the tab than the shear layer for $R = 2$. It is also interesting to note that there is not a second separation envelope at the upstream side of the jet exit for either $R = 2$ or 4.

Given these surface flow observations, we next examine the state of the jet boundary layer as it approaches the jet exit plane. The jet boundary layer momentum thickness is defined as

(8.1)\begin{equation} \theta_{{jet}} = \int_0^\delta \frac{V}{V_e} \left( 1 - \frac{V}{V_e} \right)\, {\rm d} \zeta, \end{equation}

where $V$ is the mean $y$-velocity, $\zeta$ is the radial distance from the surface of the nozzle or tab, $\delta$ is the boundary layer thickness (determined using the method of Griffin, Fu & Moin Reference Griffin, Fu and Moin2021) and $V_e$ is the vertical velocity at the edge of the boundary layer ($\zeta = \delta$). Figure 29(a,b) plots $\theta _{{jet}}$ at the jet exit plane vs $\phi$ for the non-tabbed jet (Regan & Mahesh Reference Regan and Mahesh2019), the upstream tab and the 45$^\circ$ tab. First, examination of the momentum thickness for the non-tabbed jet at $R = 2$ (figure 29a) shows that the larger magnitude of cross-flow for $R = 2$ causes an increase in boundary layer thickness at the front of the nozzle ($-45^\circ < \phi < 45^\circ$) whereas there is almost no increase for $R = 4$. The effect of the tab at both values of $R$ is to locally decrease the momentum thickness near the apex of the tab and to increase the momentum thickness on either side of the tab. While this effect locally reduces $\theta _{{jet}}$ at $\phi = 0^\circ$ for the upstream tab, it leads to an increase of $\theta _{{jet}}$ at the same location for the 45$^\circ$ tab. Harris et al. (Reference Harris, Besnard and Karagozian2021) measured the counter-current shear layer momentum thickness near the jet exit and reported that the shear layer thickness was increased for all tab configurations over the non-tabbed baseline nozzle, with the upstream tab producing the largest increase. This measurement may be influenced by the increase in momentum thickness to the sides of the tab given the 1.2 mm thick particle image velocimetry laser sheet used to extract the jet profile compared with the 1.01 mm width of the tab in the experiments.

Figure 29. Variation of jet boundary layer radial momentum thickness at the jet exit plane vs $\phi = \textrm {arctan}(-z/x)$ for $R = 2$ (a) and $R = 4$ (b). Note that $\phi = 0^\circ$ corresponds to the upstream side of the nozzle. Results for the upstream tab (———), 45$^\circ$ tab (– – – – –) and the non-tabbed jet from Regan & Mahesh (Reference Regan and Mahesh2019) ($\cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot$) are shown.

8.4. The CVP and tertiary vortex

Finally, we investigate the effect of the 45$^\circ$ tab on the evolution of the jet cross-section given the observations in § 8.2. Figure 30 shows $x$-planes at locations $x/D = 2, 4, 6, 8$ downstream of the jet exit for the 45$^\circ$ tab at $R = 2$ (top row) and $R = 4$ (bottom row). While the slices for $R = 2$ do show some slight skewing of the CVP to the negative $z$-direction, the effect is far more pronounced for $R = 4$, where the tertiary vortex is also visible. These observations echo the cross-sectional concentration measurements of Harris et al. (Reference Harris, Besnard and Karagozian2021) for $J = 7$ and $J = 61$ at $Re_j = 2300$. For the $R = 4$ case, figure 30(e) emphasizes the shear layer formed between the CVP and tertiary vortex near the jet exit at $x/D = 2$, followed by the splitting of the $+\bar {\omega }_x$ lobe of the CVP from the tertiary vortex at $x/D = 4$ (figure 30f). Further downstream, the tertiary vortex is in closest proximity to the $-\bar {\omega }_x$ lobe of the CVP, and thus entrains fluid from the $z<0$ side of the domain to be carried into the CVP. Moving from $x/D = 4$ to $x/D = 8$, the $+\bar {\omega }_x$ lobe of the CVP increasingly loses its coherence compared with the $-\bar {\omega }_x$ lobe of the CVP.

Figure 30. Evolution of the CVP along the $x$-direction for the 45$^\circ$ tab, coloured by $\bar {\omega }_x D/\bar {U}_{{jet}}$. Contour lines are also plotted for $\bar {\omega }_x D/\bar {U}_{{jet}} = \pm 0.06$. Results for $R = 2$ (a–d) and $R = 4$ (e–h) are shown.

To investigate this aspect of the cross-sectional structure for the 45$^\circ$ tab at $R = 4$, figure 31 shows contours of $x$-velocity (top row) and turbulent kinetic energy (bottom row) at the same locations as figure 30(e–h). The contours of $k$ suggest that the reduced coherence of the $+\bar {\omega }_x$ half of the CVP is due to the higher level of turbulence in this lobe of the CVP, a phenomenon that persists far downstream of the jet exit. Particularly interesting are the contours of $\bar {u}/U_{\infty }$ (figure 31a–d), which show that the $+\bar {\omega }_x$ lobe of the CVP has a velocity that is consistently higher than the cross-flow velocity, while the $-\bar {\omega }_x$ lobe of the CVP and tertiary vortex have a much lower velocity than the cross-flow. While the $x$-velocity of the tertiary vortex begins to recover by $x/D = 8$, the $-\bar {\omega }_x$ lobe of the CVP still exhibits a very low $x$-velocity at the centre of the vortex core at $x/D = 8$.

Figure 31. Evolution of the CVP along the $x$-direction for the 45$^\circ$ tab at $R = 4$, with contours of $\bar {u}/U_{\infty }$ (a–d) and $k/\bar {U}_{{jet}}$ (e–h). Contour lines of $\bar {\omega }_x D/\bar {U}_{{jet}} = \pm 0.06$ are also shown on each plot to visualize the CVP and tertiary vortex locations.