Dip coating is a common technique used to cover a solid surface with a thin liquid film, the thickness of which was successfully predicted by the theory developed in the 1940s by Landau & Levich (Acta Physicochem. URSS, vol. 17, 1942, pp. 141–153) and Derjaguin (Acta Physicochem. URSS, vol. 20, 1943, pp. 349–352). In this work, we present an extension of their theory to the case where the dipping bath contains two immiscible liquids, one lighter than the other, resulting in the entrainment of two thin films on the substrate. We report how the thicknesses of the coated films depend on the capillary number, on the ratios of the properties of the two liquids and on the relative thickness of the upper fluid layer in the bath. We also show that the liquid/liquid and liquid/gas interfaces evolve independently from each other as if only one liquid were coated, except for a very small region where their separation falls quickly to its asymptotic value and the shear stresses at the two interfaces peak. Interestingly, we find that the final coated thicknesses are determined by the values of these maximum shear stresses.

Rotations of spheroidal particles immersed in turbulent flows reflect the combined effects of fluid strain and vorticity, as well as the time history of these quantities along the particle's trajectory. Conversely, particle rotation statistics in turbulence provide a way to characterise the Lagrangian properties of velocity gradients. Particle rotations are also important for a range of environmental and industrial processes where particles of various shapes and sizes are immersed in a turbulent flow. In this study, we investigate the rotations of inertialess spheroidal particles that follow Lagrangian fluid trajectories. We perform direct numerical simulations (DNS) of homogeneous isotropic turbulence and investigate the dynamics of different particle shapes at different scales in turbulence using a filtering approach. We find that the mean-square particle angular velocity is nearly independent of particle shape across all scales from the Kolmogorov scale to the integral scale. The particle shape does determine the relative split between different modes of rotation (spinning vs tumbling), but this split is also almost independent of the filter scale suggesting a Lagrangian scale-invariance in velocity gradients. We show how the split between spinning and tumbling can be quantitatively related to the particle's alignment with respect to the fluid vorticity.

Cavitating flows include vapour structures with a wide range of different length scales, from micro-bubbles to large cavities. The correct estimation of small-scale cavities can be as important as that of large-scale structures, because cavitation inception as well as the resulting noise, erosion and strong vibrations occur at small time and length scales. In this study, a multi-scale cavitating flow around a sharp-edged bluff body is investigated. For numerical analysis, while popular homogeneous mixture models are practical options for large-scale applications, they are normally limited in the representation of small-scale cavities. Therefore, a hybrid cavitation model is developed by coupling a mixture model with a Lagrangian bubble model. The Lagrangian model is based on a four-way coupling approach, which includes new submodels, to consider various small-scale phenomena in cavitation dynamics. Additionally, the coupling of the mixture and the Lagrangian models is based on an improved algorithm that is compatible with the flow physics. The numerical analysis provides a detailed description of the multi-scale dynamics of cavities as well as the interactions between vapour structures of various scales and the continuous flow. The results, among others, show that small-scale cavities not only are important at the inception and collapse steps, but also influence the development of large-scale structures. Furthermore, a comparison of the results with those from experiment shows considerable improvements in both predicting the large cavities and capturing the small-scale structures using the hybrid model. More accurate results (compared with the traditional mixture model) can be achieved even with a lower mesh resolution.

We study the convective and absolute forms of azimuthal magnetorotational instability (AMRI) in a cylindrical Taylor–Couette (TC) flow with an imposed azimuthal magnetic field. We show that the domain of the convective AMRI is wider than that of the absolute AMRI. Actually, it is the absolute instability which is the most relevant and important for magnetic TC flow experiments. The absolute AMRI, unlike the convective one, stays in the device, displaying a sustained growth that can be experimentally detected. We also study the global AMRI in a TC flow of finite height using direct numerical simulation and find that its emerging butterfly-type structure – a spatio-temporal variation in the form of axially upward and downward travelling waves – is in a very good agreement with the linear analysis, which indicates the presence of two dominant absolute AMRI modes in the flow giving rise to this global butterfly pattern.

The ability of microswimmers to deploy optimal propulsion strategies is of paramount importance for their locomotory performance and survival at low Reynolds numbers. Although for perfectly spherical swimmers minimum dissipation requires a neutral-type swimming, any departure from the spherical shape may lead the swimmer to adopt a new propulsion strategy, namely those of puller- or pusher-type swimming. In this study, by using the minimum dissipation theorem for microswimmers, we determine the flow field of an optimal nearly spherical swimmer, and show that indeed depending on the shape profile, the optimal swimmer can be a puller, pusher or neutral. Using an asymptotic approach, we find that amongst all the modes of the shape function, only the third mode determines, to leading order, the swimming type of the optimal swimmer.

Jets in crossflow are a recurring flow configuration in many engineering applications and have been the subject of many computational and experimental investigations. While these studies have identified the jet-to-crossflow velocity ratio $R$ as a critical parameter for the global stability and mixing behaviour which ultimately leads to breakdown into turbulence, a far less studied, but equally determining, factor is the presence of chemical reactions. Understanding and quantifying the nature of intrinsic instabilities in reacting and non-reacting flows and their dependence on the governing flow parameters are paramount to devising optimal designs or effective control strategies. In this study, we concentrate on the effect of reactions on the flow behaviour and extract optimal forcing and response functions for a range of driving frequencies, juxtaposing the reactive and non-reactive configurations. Simulations are performed using a compressible framework with a free-stream Mach number of $0.2$, and a constant jet-to-crossflow ratio of three. The flow configuration is kept identical for the reactive and non-reactive cases in order to isolate the effect of combustion on the resulting optimal forcing and response solutions. The frequency response is extracted using an adjoint-based optimization formalism. The presence of reactions markedly impacts the dominant frequencies of the flow. The inert case shows forcing and response modes, whose support aligns with the shear layer – as would be expected from a globally unstable jet. However, the analogous forcing functions for the reactive case concentrate around the flame, in accordance with combustion instabilities.

In this work, two-phase flows of Newtonian and/or viscoelastic fluids in a ‘cross-slot’ geometry are investigated both experimentally and numerically in the creeping-flow limit. A series of microfluidic experiments – using Newtonian fluids – have been carried out in different cross-section aspect ratios to support our numerical simulations. The numerical simulations rely on a volume of fluid method and make use of a log-conformation formulation in conjunction with the simplified viscoelastic Phan-Thien and Tanner model. Downstream from the central cross, once the flow has become fully developed, we also estimate analytically the thickness of each fluid layer for both two- and three-dimensional cases. In addition to providing a benchmark test for our numerical solver, these analytical results also provide insight into the role of the viscosity ratio. Injecting two fluids with different elastic properties from each inlet arm is shown to be an effective approach to stabilize the purely elastic instability observed in the cross-slot geometry based on the properties of the fluid with the larger relaxation time. Our results show that interfacial tension can also play an important role in the shape of the interface of the two fluids near the free-stagnation point (i.e. in the central cross). By reducing the interfacial tension force, the interface of the two fluids becomes curved and this can consequently change the curvature of streamlines in this region which, in turn, can modify the purely elastic flow transitions. Thus, increasing interfacial tension is shown to have a stabilizing effect on the associated steady symmetry-breaking purely elastic instability. However, at high values of the viscosity ratio, a new time-dependent purely elastic instability arises most likely due to the change in streamline curvature observed under these conditions. Even when both fluids are Newtonian, outside of the two-dimensional limit, a weak instability arises such that the fluid interface in the depth (neutral) direction no longer remains flat.

When a rising bubble in a Newtonian liquid reaches the liquid–air interface, it can burst, leading to the formation of capillary waves and a jet on the surface. Here, we numerically study this phenomenon in a yield-stress fluid. We show how viscoplasticity controls the fate of these capillary waves and their interaction at the bottom of the cavity. Unlike Newtonian liquids, the free surface converges to a non-flat final equilibrium shape once the driving stresses inside the pool fall below the yield stress. Details of the dynamics, including flow energy budgets, are discussed. The work culminates in a regime map with four main regimes, all with different characteristic behaviours.

We examine the effects of horizontally layered heterogeneities on the spreading of two-phase gravity currents in a porous medium, with application to numerous environmental flows, most notably geological carbon sequestration. Heterogeneities, which are ubiquitous within geological reservoirs, affect the large-scale propagation of two-phase flows through the action of small-scale capillary forces, yet the relationship between these small- and large-scale processes is poorly understood. Here, we derive a simple upscaled model for a gravity current under an impermeable cap rock, which we use to investigate the effect of a wide range of centimetre-scale heterogeneities on kilometre-scale plume migration. By parameterising in terms of different types of archetypal layering, we assess the sensitivity of the gravity current to the distribution and magnitude of these heterogeneities. Furthermore, since field measurements of heterogeneities are often sparse or incomplete, we quantify how uncertainty in such measurements manifests as uncertainty in the macroscale flow predictions. Using realistic parameter values, we demonstrate that heterogeneities can enhance plume migration speeds by as much as 200 %, and that uncertainty in field measurements can have dramatic consequences on flow predictions, particularly in post-injection scenarios where the role of capillary forces in heterogeneities is accentuated.

We show that the Stokes–Darcy system, which governs flows through adjacent porous and pure-fluid domains in the two-domain approach without forced filtration, can be recovered from the Helmholtz minimal dissipation principle. While the continuity of normal velocity across the interface is imposed explicitly for mass conservation, only the Beavers–Joseph–Saffman–Jones (BJSJ) interface boundary condition is imposed implicitly, and the balance of the normal-force interface boundary condition appears naturally in the variational process. This set of interface boundary conditions is well-accepted in the mathematics community. We show that these interfacial boundary conditions, at the physically important small-Darcy-number regime, are consistent with continuity of pressure across the interface condition. The tangential velocity and pressure are discontinuous in general but the discontinuity is of the order of the square root of the Darcy number. Hence these interfacial conditions are all approximately consistent in the physically important small-Darcy-number regime. The leading order dynamics in the pure fluid zone is governed by the Stokes system with the no-slip no-penetration boundary condition on the interface between the free zone and porous media at a small Darcy number. The leading order non-trivial dynamics in porous media is governed by the Darcy equation with the pressure on the interface prescribed by the pressure of the leading order Stokes flow in the pure fluid zone. Such a semi-decoupled approach has long been used by the groundwater community. Our result is the first rigorous work quantifying the error of this intuitive approach and relating different interfacial conditions.

This paper addresses peristaltic flow induced in a non-axisymmetric annular tube by a periodic small-amplitude wave of arbitrary shape propagating axially along its inner surface, assumed to be a circular cylinder. The study is motivated by recent in vivo experimental observations pertaining to the flow of cerebrospinal fluid along the perivascular spaces of cerebral arteries. The analysis employs the lubrication approximation, describing low-Reynolds-number peristaltic flow in the long-wavelength approximation. Closed-form analytic expressions are derived for the average pumping rate in infinitely long tubes and also in tubes of finite length. Consideration is also given to the transverse motion arising in non-axisymmetric tubes. For small-amplitude waves, the solution is reduced to the integration of a parameter-free Stokes-flow problem, which is solved for relevant cross-sectional shapes, with closed-form analytical results derived for thin canals.

Motivated by observations of turbulence in the strongly stratified ocean thermocline, we use direct numerical simulations to investigate the interaction of a sinusoidal shear flow and a large-amplitude internal gravity wave. Despite strong nonlinearities in the flow and a lack of scale separation, we find that linear ray-tracing theory is qualitatively useful in describing the early development of the flow as the wave is refracted by the shear. Consistent with the linear theory, the energy of the wave accumulates in regions of negative mean shear where we observe evidence of convective and shear instabilities. Streamwise-aligned convective rolls emerge the fastest, but their contribution to irreversible mixing is dwarfed by shear-driven billow structures that develop later. Although the wave strongly distorts the buoyancy field on which these billows develop, the mixing efficiency of the subsequent turbulence is similar to that arising from Kelvin–Helmholtz instability in a stratified shear layer. We run simulations at Reynolds numbers Re of 5000 and 8000, and vary the initial amplitude of the internal gravity wave. For high values of initial wave amplitude, the results are qualitatively independent of $Re$. Smaller initial wave amplitudes delay the onset of the instabilities, and allow for significant laminar diffusion of the internal wave, leading to reduced turbulent activity. We discuss the complex interaction between the mean flow, internal gravity wave and turbulence, and its implications for internal wave-driven mixing in the ocean.

We present a detailed comparison of the rheological behaviour of sheared sediment beds in a pressure-driven, straight channel configuration based on data that were generated by means of fully coupled, grain-resolved direct numerical simulations and experimental measurements previously published by Aussillous et al. (J. Fluid Mech., vol. 736, 2013, pp. 594–615). The highly resolved simulation data allow us to compute the stress balance of the suspension in the streamwise and vertical directions and the stress exchange between the fluid and particle phases, which is information needed to infer the rheology, but has so far been unreachable in experiments. Applying this knowledge to the experimental and numerical data, we obtain the statistically stationary, depth-resolved profiles of the relevant rheological quantities. The scaling behaviour of rheological quantities such as the shear and normal viscosities and the effective friction coefficient are examined and compared to data coming from rheometry experiments and from widely used rheological correlations. We show that rheological properties that have previously been inferred for annular Couette-type shear flows with neutrally buoyant particles still hold for our set-up of sediment transport in a Poiseuille flow and in the dense regime we found good agreement with empirical relationships derived therefrom. Subdividing the total stress into parts from particle contact and hydrodynamics suggests a critical particle volume fraction of 0.3 to separate the dense from the dilute regime. In the dilute regime, i.e. the sediment transport layer, long-range hydrodynamic interactions are screened by the porous medium and the effective viscosity obeys the Einstein relation.

Microorganisms may exhibit rich swimming behaviours in anisotropic fluids, such as liquid crystals, which have direction-dependent physical and rheological properties. Here we construct a two-dimensional computation model to study the undulatory swimming mechanisms of microswimmers in a solution of rigid, rodlike liquid crystal polymers. We describe the fluid phase using Doi's $Q$-tensor model, and treat the swimmer as a finite-length flexible fibre with imposed propagating travelling waves on the body curvature. The fluid–structure interactions are resolved via an immersed boundary method. Compared with the swimming dynamics in Newtonian fluids, we observe non-Newtonian behaviours that feature both enhanced and retarded swimming motions in lyotropic liquid crystal polymers. We reveal the propulsion mechanism by analysing the near-body flow fields and polymeric force distributions, together with asymptotic analysis for an idealized model of Taylor's swimming sheet.

We investigate the dynamics of cohesive particles in homogeneous isotropic turbulence, based on one-way coupled simulations that include Stokes drag, lubrication, cohesive and direct contact forces. We observe a transient flocculation phase, followed by a statistically steady equilibrium phase. We analyse the temporal evolution of floc size and shape due to aggregation, breakage and deformation. Larger turbulent shear and weaker cohesive forces yield smaller elongated flocs. Flocculation proceeds most rapidly when the fluid and particle time scales are balanced and a suitably defined Stokes number is $O(1)$. During the transient stage, cohesive forces of intermediate strength produce flocs of the largest size, as they are strong enough to cause aggregation, but not so strong as to pull the floc into a compact shape. Small Stokes numbers and weak turbulence delay the onset of the equilibrium stage. During equilibrium, stronger cohesive forces yield flocs of larger size. The equilibrium floc size distribution exhibits a preferred size that depends on the cohesive number. We observe that flocs are generally elongated by turbulent stresses before breakage. Flocs of size close to the Kolmogorov length scale preferentially align themselves with the intermediate strain direction and the vorticity vector. Flocs of smaller size tend to align themselves with the extensional strain direction. More generally, flocs are aligned with the strongest Lagrangian stretching direction. The Kolmogorov scale is seen to limit floc growth. We propose a new flocculation model with a variable fractal dimension that predicts the temporal evolution of the floc size and shape.

The theoretical existence of the granular monoclinal wave, based on the Saint-Venant equations for flowing granular matter, was reported recently by Razis et al. (J. Fluid Mech., vol. 843, 2018, pp. 810–846). The present paper focuses on the mathematical interpretation of its behaviour, treating the equation of motion that describes any granular waveform as a dynamical system, taking also into consideration the Froude number offset 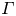$\varGamma$ introduced by Forterre & Pouliquen (J. Fluid Mech., vol. 486, 2003, pp. 21–50). The critical value of the Froude number below which stable uniform flows are observed is determined directly from the stability analysis of the aforementioned dynamical system. It is shown that the granular monoclinal wave, represented as a heteroclinic orbit in phase space, can be categorized into two classes: (i) the mild class, for which the exact form of the waveform can be approximated by the non-viscous (first-order) adaptation of the granular Saint-Venant equations, and (ii) the steep class, for a description of which a second-order (viscous) term in the Saint-Venant equations is absolutely needed to capture the dynamics of the wave. The mathematical criterion that distinguishes the two classes is the changing sign of the trace of the Jacobian matrix evaluated at the fixed point corresponding to the waveform's lower plateau.

Viscous drops, subject to a linear flow in an immiscible viscous fluid, deform. When the resulting drop shape is simple the problem can be addressed by an asymptotic approach or by approximating the deformation using known simple shapes. When the resulting deformation is more complex, the problem is usually addressed numerically. In this paper, we address the problem of drops that are deforming in an axisymmetric compressional (bi-axial extensional) flow. Yielded shapes are flat drops, flat drops with dimples and toroidal drops. The latter two are highly unstable. We propose to approximate the solution of this problem, approximating the shapes by using generalized Cassini ovals, defined herein. The analysis reproduced the branches with shapes of stationary stable flat drops and stationary unstable toroidal drops, available from numerical calculation. Furthermore, it predicts the point of loss of stability of the flat drop to exhibit the transition branch that leads into the formation of the toroidal shapes, and shows that this branch shows stationary, yet unstable, flat drops with ever growing dimples up to collapse.

Oscillatory flows have the potential to overcome long-standing limitations encountered when using steady flows for inertial focusing due to low particle Reynolds numbers. The periodic displacement generated by oscillatory flow increases the total path length travelled by a suspended particle with no net displacement within a channel or the need for increased channel length. The effects of unsteady inertial forces on inertial focusing, however, have not been thoroughly examined. Here, we present a combined theoretical and experimental study on the effect of Womersley number on inertial focusing in planar pulsatile flows. The migration velocity for a small and weakly inertial particle was evaluated for different oscillation frequencies using the method of matched asymptotics. Using experiments in a custom-built microchannel, we show that oscillatory flows are remarkably efficient for inertial focusing, even at low particle Reynolds numbers. For appropriately selected oscillation amplitude and frequency, inertial focusing is achieved in only a fraction of the channel length (1 % to 10 %) compared to what would be required in a steady flow. We show that the Womersley number influences the equilibrium focusing position and the overall focusing efficiency. In fact, above a critical Womersley number, inertial focusing does not occur despite increasing particle Reynolds number. Lastly, the application of oscillatory inertial focusing for the direct measurement of particle migration velocity is demonstrated.

The impact of a drop train, a series of identical liquid drops separated by a constant distance, on a liquid pool initially generates a long slender cavity. However, the cavity soon collapses and turns into a shallow funnel. Here we theoretically model the dynamic profile of the elongated cavity and the steady shape of the funnel, which are then shown to agree well with experiment. When the liquid inertia plays a dominant role, the cavity assumes a parabolic profile that depends only on the drop diameter and the centre-to-centre spacing of adjacent drops. We consider the capillary forces as well as the drop impact force to obtain the shape of the funnel that persists once the elongated cavity collapses. Our study allows for predicting the interfacial morphology by the impact of a drop train and designing impact conditions useful for semiconductor cleaning processes.

We prove a new explicit inequality for the non-dimensional flow force constant, significantly improving the Benjamin and Lighthill conjecture about irrotational steady water waves. As a corollary, we prove a bound for the wave amplitude in terms of the Bernoulli constant. We show that the amplitude decays as $r^{-2}$ when $r \to +\infty$, where $r$ is the non-dimensional Bernoulli constant. We explain that the latter limit corresponds to deep water waves and the bound for the amplitude is sharp. In terms of physical parameters the result states that the amplitude $a$ of an arbitrary Stokes wave is bounded by $C m^2 g/Q^2$, where $m$ is the relative mass flux, $g$ is the gravitational constant, $Q$ is the total head and $C$ is an absolute constant given explicitly. In particular, this implies that $a < C c^2 g^{-1}$, where $c$ is the wave speed. The latter inequality is valid for all Stokes waves, irrespective of wavelength or amplitude, including extreme waves.