We present an experimental and numerical investigation of electrokinetic instability (EKI) in microchannel flow with streamwise conductivity gradients, such as those observed during sample stacking in capillary electrophoresis. A plug of a low-conductivity electrolyte solution is initially sandwiched between two high-conductivity zones in a microchannel. This spatial conductivity gradient is subjected to an external electric field applied along the microchannel axis, and for sufficiently strong electric fields an instability sets in. We have explored the physics of this EKI through experiments and numerical simulations, and supplemented the results using scaling analysis. We performed EKI experiments at different electric field values and visualised the flow using a passive fluorescent tracer. The experimental data were analysed using the proper orthogonal decomposition technique to obtain a quantitative measure of the threshold electric field for the onset of instability, along with the corresponding coherent structures. To elucidate the physical mechanism underlying the instability, we performed high-resolution numerical simulations of ion transport coupled with fluid flow driven by the electric body force. Simulations reveal that the non-uniform electroosmotic flow due to axially varying conductivity field causes a recirculating flow within the low-conductivity region, and creates a new configuration wherein the local conductivity gradients are orthogonal to the applied electric field. This configuration leads to EKI above a threshold electric field. The spatial features of the instability predicted by the simulations and the threshold electric field are in good agreement with the experimental observations and provide useful insight into the underlying mechanism of instability.

When a mixture of viscous oil and non-colloidal particles displaces air between two parallel plates, the shear-induced migration of particles leads to the gradual accumulation of particles on the advancing oil–air interface. This particle accumulation results in the fingering of an otherwise stable fluid–fluid interface. While previous works have focused on the resultant instability, one unexplored yet striking feature of the experiments is the self-similarity in the concentration profile of the accumulating particles. In this paper, we rationalise this self-similar behaviour by deriving a depth-averaged particle transport equation based on the suspension balance model, following the theoretical framework of Ramachandran (J. Fluid Mech., vol. 734, 2013, pp. 219–252). The solutions to the particle transport equation are shown to be self-similar with slight deviations, and in excellent agreement with experimental observations. Our results demonstrate that the combination of the shear-induced migration, the advancing fluid–fluid interface and Taylor dispersion yield the self-similar and gradual accumulation of particles.

Utilizing the joint singular natures of electric field and hydrodynamic flow around a sharp nanotip, we report new electrohydrodynamic Landau–Squire-type flows under the actions of alternating current (AC) electric fields, markedly different from the classical Landau–Squire flow generated by pump discharge using nanotubes or nanopores. Making use of the locally diverging electric field prevailing near the conical tip, we are able to generate a diversity of AC electrohydrodynamic flows with the signature of a 1/r point-force-like decay at distance r from the tip. Specifically, we find AC electrothermal jet and Faradaic streaming out of the tip at applied frequencies in the MHz and 102 Hz regimes, respectively. Yet at intermediate frequencies of 1–100 kHz, the jet flow can be reversed to an AC electro-osmotic impinging flow. The characteristics of these AC jet flows are very distinct from AC flows over planar electrodes. For the AC electrothermal jet, we observe experimentally that its speed varies with the driving voltage V as V3, in contrast to the common V4 dependence according to the classical theory reported by Ramos et al. (J. Phys. D: Appl. Phys, vol. 31, 1998, pp. 2338–2353). Additionally, the flow speed does not increase with the solution conductivity as commonly thought. These experimental findings can be rationalized by means of local Joule heating and double layer charging mechanisms in such a way that the nanotip actually becomes a local hotspot charged with heated tangential currents. The measured speed of the AC Faradaic streaming is found to vary as V3/2 logV, which can be interpreted by the local Faradaic leakage in balance with tangential conduction. These unusual flow characteristics signify that a conical electrode geometry may fundamentally alter the features of AC electrohydrodynamic flows. Such peculiar electrohydrodynamic flows may also provide new avenues for expediting molecular sensing or sample transport in prevalent electrochemical or microfluidic applications.

Bubble-laden thermals provide a formidable gas transport mechanism responsible, for instance, for the explosive foaming-up process during the beer tapping prank, or the infamous gas eruption of Lake Nyos in 1986. In this work we investigate experimentally the growth and motion of laser-induced turbulent thermals in a carbonated water solution with surfactants. One of the novelties of this study is that we are able to quantify with high temporal resolution the rate at which the gas volume contained in the bubbles grows. After an initial transient stage, the gas bubble and entrained liquid volumes of the thermal both grow as a cubic power of time. The buoyancy generation rate is well explained by the mass transfer scaling expected for individual bubbles. In contrast, the thermal rise velocity does not adhere to any particular scaling law. These facts lie in qualitative agreement with a phenomenological model, based on classical models for turbulent thermals, that takes into account buoyancy generation.

The electrophoretic motion of a non-uniformly charged particle in an Oldroyd-B fluid is analysed here in the limit of thin electrical double layers. To this end, we analytically derive expressions for the modified Smoluchowski slip velocity around the particle, carrying weak but otherwise arbitrary surface charge. Our analysis reveals that the modified Smoluchowski slip around a particle differs significantly in a viscoelastic medium as compared with Newtonian fluids. The flow field thus derived is applied to two special cases of non-uniformly charged particles to obtain a closed-form expression for their electrophoretic translational and rotational velocities. We show that the particle's velocity strongly depends on its size in a viscoelastic medium, even for weakly charged surfaces, which is in stark contrast to the well-established theory for Newtonian fluids for weakly charged particles with negligible surface conduction. We further demonstrate that the presence of non-uniform surface charge enhances the influence of the medium's viscoelasticity on the particle's translational as well as angular velocity and this effect strongly depends on the nature of surface charge distribution. Such a physical paradigm, which leads to a breaking of fore–aft symmetry that is unique to complex fluids despite operating in the regime of creeping flows. Our study provides new theoretical framework for understanding electrophoresis of charged entities (such as DNA or active matter) in complex fluids, including biologically relevant fluidic media.

We experimentally observe and theoretically analyse oscillations of a spherical bubble in a gelatin gel under ultrasound irradiation to quantify viscoelastic effects on the nonlinear bubble dynamics. A bubble nucleus is generated by focusing a laser pulse into a 6 wt% gelatin gel supersaturated with dissolved air, which enables us to control the bubble radius at mechanical equilibrium via influx of the gas air into the bubble. Linearized and finite-amplitude oscillations of the bubble are driven by 28 kHz ultrasound and recorded by a high-speed camera; the resonance curves of the oscillation amplitude as a function of the equilibrium radius are constructed for different ultrasound intensities. First, the viscosity and shear modulus of the gel are obtained by fitting the resonance curve (for the lowest ultrasound intensity) to the linearized solution of the Rayleigh–Plesset model that accounts for the gel's nonlinear elasticity of neo-Hookean type and diffusive effects on the bubble dynamics. Next, finite-amplitude oscillations of the bubble are compared with the nonlinear Rayleigh–Plesset calculations. The comparison suggests a need to include the gel's elasticity in the calculations to more accurately reproduce the nonlinear bubble dynamics. Another important finding is that the so-called spring softening feature appears in the experimentally determined resonance curve as the oscillation amplitude increases, which can be predicted by the Rayleigh–Plesset model. Furthermore, our experiment with the highest ultrasound intensity shows non-spherical oscillation of mode 1 that does not appear in the case of water but can be predicted by shape instability theory.

The propagation of a normal shock wave along a coupled convex–concave surface of equal radii has been analysed experimentally and numerically in this study. The experimental and numerical studies were conducted using a similar geometry as of that used by Ram et al. (J. Fluid Mech., vol. 768, 2015, pp. 219–239) for studying the shock wave transition from regular reflection to Mach reflection. Many interesting flow features such as shock wave transitions over the ramp, characteristics of the induced flow behind the shock wave and the development of a stationary separation shock wave have been observed in the study. The numerical results are validated with experimental data. While the shock wave transitions over the ramp are found to depend mainly on the ramp geometry, the characteristics of the stationary shock wave and the flow separation in the concave region of the ramp surface have been found to vary with the shock wave Mach numbers.

The theoretical limit for absorption of energy in monochromatic water waves of wavelength $\lambda$ by axisymmetric wave energy converters operating in rigid-body motion was established in the 1970s. The maximum mean power generated by a device absorbing due to heave motion is equivalent to that contained in $\lambda /2{\rm \pi}$ length of an incident wave crest. For devices absorbing through surge and/or pitch motions the so-called capture width doubles to $\lambda /{\rm \pi}$. For devices absorbing in both heave and surge/pitch the capture width increases further to $3\lambda /2{\rm \pi}$. In this paper it is demonstrated that it is theoretically possible to extend the capture width for axisymmetric wave energy converters without bound through the use of generalised (non-rigid-body) modes of motion. This concept is applied to vertical cylinders whose surface is surrounded by an array of narrow vertical absorbing paddles. A continuum approximation is made to the paddle motion which simplifies the problem and allows strategies to be developed for setting the springs and dampers that control the power absorption. Results demonstrate that a cylinder of fixed size can absorb as much power as demanded from a plane incident wave although the practical limitations of linear theory are rapidly breached as that demand increases unless the size of the cylinder increases in proportion. In this paper we do not explore these limits in detail or further practical design considerations, such as imposing motion constraints. The continuum approximation is tested against a discrete paddle simulation for accuracy.

The wetting or dewetting of a solid substrate by a liquid involves the motion of the contact line between the two phases. One of the parameters that govern the dynamics of the flow near a moving contact line is the local Reynolds number, 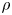$\rho$. At sufficient proximity to the moving contact line, where 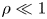$\rho \ll 1$, the flow is dominated by viscous forces over inertia. However, further away from the contact line, or at higher speeds of motion, inertia is also expected to be influential. In such cases, the current contact line models, which assume Stokes flow and neglect inertia entirely, would be inaccurate in describing the hydrodynamic flow fields. Hence, to account for inertia, here we perform a regular perturbation expansion in 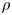$\rho$, of the streamfunction near the Stokes solution. We, however, find that the leading-order inertial correction thus obtained is singular at a critical contact angle of 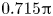$0.715 {\rm \pi}$. We resolve this spurious mathematical singularity by incorporating the eigenfunction terms, which physically represent flows due to disturbances originating far from the contact line. In particular, we propose a stick slip on the solid boundary – arising from local surface heterogeneities – as the mechanism that generates these disturbance flows. The resulting singularity-free, inertia-corrected streamfunction shows significant deviation from the Stokes solution in the visco-inertial regime (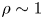$\rho \sim 1$). Furthermore, we quantify the effect of inertia by analysing its contribution to the velocity at the liquid interface. We also provide the leading-order inertial correction to the dynamic contact angles predicted by the classical Cox–Voinov model; while inertia has considerable effect on the hydrodynamic flow fields, we find that it has little to no influence on the dynamic contact angles.

The impact of a forward-facing step (FFS) on the development of stationary crossflow instability is investigated on a swept wing model in a low-turbulence wind tunnel at chord Reynolds number of $2.3 \times 10^{6}$. Infrared thermography and particle image velocimetry measurements are used to quantify the transition location and growth of the crossflow instability under the influence of FFSs with different heights. Forced monochromatic stationary crossflow vortices experience an abrupt change in their trajectory as they interact with the step geometry. As the boundary layer intercepts the step an increase in the vertical velocity component and an amplification of the crossflow vortices is observed. Near the step, the vortices reach maximum amplification, while dampening downstream. The smaller FFS cases, show a local stabilising effect on the primary stationary mode and its harmonics, while in the higher step cases transition occurs. The analysis of the temporal velocity fluctuations shows a reduction in the region associated with the type-III travelling crossflow modes downstream of the step. In contrast, the velocity fluctuations in the region associated with type-I secondary instabilities increase past the FFS edge. Nonetheless, in the shortest FFS cases, these velocity fluctuations eventually decay below the clean configuration (i.e. without an FFS) levels. This behaviour is linked to a novel transition delay effect for the shortest step height investigated. The findings highlight new physical aspects driving the interaction between an amplified stationary crossflow vortex and an FFS and provide insight into possible transition delay mechanisms using such geometries.

Turbulent plane Poiseuille and Couette flows share the same geometry, but produce their flow rate owing to different external drivers: pressure gradient and shear, respectively. By looking at integral energy fluxes, we pose and answer the question as to which flow performs better at creating flow rate. We define a flow efficiency, which quantifies the fraction of power used to produce flow rate instead of being wasted as a turbulent overhead; effectiveness, instead, describes the amount of flow rate produced by a given power. The work by Gatti et al. (J. Fluid Mech., vol. 857, 2018, pp. 345–373), where the constant power input concept was developed to compare turbulent Poiseuille flows with drag reduction, is here extended to compare different flows. By decomposing the mean velocity field into a laminar contribution and a deviation, analytical expressions are derived which are the energy-flux equivalents of the FIK identity. These concepts are applied to literature data supplemented by a new set of direct numerical simulations, to find that Couette flows are less efficient but more effective than Poiseuille flows. The reason is traced to the more effective laminar component of Couette flows, which compensates for their higher turbulent activity. It is also observed that, when the fluctuating fields of the two flows are fed with the same total power fraction, Couette flows dissipate a smaller percentage of it via turbulent dissipation. A decomposition of the fluctuating field into large and small scales explains this feature: Couette flows develop stronger large-scale structures, which alter the mean flow while contributing less significantly to dissipation.

Translation of a non-spherical particle trapped at a membrane or at a complex interface between fluids is a relevant situation occurring in biological, technological and everyday life systems. Here, we consider prolate spheroidal particles, translating at a clean or (insoluble) surfactant-laden planar interface located between a viscous fluid and air, protruding into the surrounding subphase. Both the subphase and monolayer contribute to the total resistance experienced by the particle, which in turn is a function of interface and bulk viscosities, particle size and aspect ratio as well as the immersion depth of the particle. We explore how the drag on a spheroidal particle at a viscous interface can both rise or decrease with particle size depending on the dimensionless Boussinesq and Marangoni numbers. For a surfactant-laden interface, the surfactant distribution in the vicinity of the moving spheroid is significantly affected by the particle's immersion depth. When a particle sinks more in the viscous fluid, as determined by the involved surface tensions, the difference in surfactant concentration between front and rear of the particle decreases. For the drag coefficient of a spherical particle at an incompressible interface at low shear Boussinesq numbers, we propose a correction to previously reported analytic expressions. We probe both parallel and perpendicular friction coefficients as they are significantly different depending on particle shape, qualitatively different depending on surface shear viscosity, and we resolve the full three-dimensional distortion of the flow field around the moving particle.

As a first step towards the description of coherent structures in compressible shear flows, we present an asymptotic description of nonlinear travelling-wave solutions of the Navier–Stokes equations in the compressible asymptotic suction boundary layer (ASBL). We consider free-stream Mach numbers $M_\infty$ in the subsonic and moderate supersonic regime so that $0\leqslant M_\infty \leqslant 2$. We extend the large-Reynolds-number asymptotic theory of Deguchi & Hall (J. Fluid Mech., vol. 752, 2014, pp. 602–625) describing ‘free-stream’ coherent structures in incompressible ASBL flow to describe a nonlinear interaction in a thin layer situated just below the free stream. Crucially, the nonlinear interaction equations for the velocity field in this layer are identical to those obtained in the incompressible problem, and thus the asymptotic analysis supporting free-stream coherent structures in compressible ASBL is easily deduced from its incompressible counterpart. The nonlinear interaction produces streaky disturbances to both the velocity and temperature fields, which can grow exponentially towards the wall. We complete the description of the growth of the velocity and thermal streaks throughout the flow by solving the compressible boundary-region equations numerically. We show that the velocity and thermal streaks obtain their maximum amplitude in the unperturbed boundary layer. Increasing the free-stream Mach number enhances the thermal streaks and suppresses the velocity streaks, whereas varying the Prandtl number suppresses the velocity streaks, and can either enhance or suppress the thermal streaks depending on whether the flow is in the subsonic or moderate supersonic regime. Such nonlinear equilibrium states have been implicated in shear transition in incompressible flows; therefore, our results indicate that a similar mechanism may also be present in compressible flows.

Highly turbulent free-surface flows are characterised by complex and rapidly varying air–water surface features, leading to enhanced surface roughness, breakup and disintegration processes. Such a strong free-surface turbulence has an impact on a number of environmental flows, and a deeper understanding of its physical nature is fundamental. Unsteady breaking bores are of particular interest because of their recirculating motion, with large air entrainment and splashes, resulting in highly fluctuating and rapidly varying free-surface flows. Herein, new methodologies and innovative approaches are used in support of a deeper understanding of the physical processes within a breaking roller, inclusive of a comprehensive assessment of its free-surface dynamics. Because of the unsteadiness of the flow, multiple repetitions were necessary and all results were based upon an ensemble statistical analysis. Ultra-high-speed videos recorded from both top and side views allowed for a detailed characterisation of the roller's free surface, providing a description and classification of the most recurring air–water surface features. A quantification of their main properties in terms of geometry, duration and frequency of appearance revealed an evolution of these features during their lifespans. In parallel, the use of optical flow techniques provided a characterisation of the surface velocity fields, yielding information on the free-surface kinematic properties and revealing a strong link between air–water surface features, energy dissipation and time/length scales.

Mechanical degradation of macromolecules in strong flows is encountered in many industrial processes spanning from biopharmaceutics manufacturing to enhanced oil recovery. In spite of extensive research, from molecular studies to large experiments, unifying scaling laws and design rules to harness this phenomenon are still at an early stage. Some of the current modelling approaches predict the onset of flow-induced degradation only, leaving out quantitative calculations of scission events, while others are restricted to a particular process or the materials they have been empirically developed for. In this work we re-examine a previously published constitutive equation for the scission kinetics of polymers and implement the model using the finite volume library OpenFoam. We test and validate this model using experimental degradation measurements of aqueous poly(ethylene oxide) solutions flowing through narrow constrictions. Three polymer molecular weights and three constriction geometries are investigated. For each molecular weight, experimental degradation data of one geometry is used to calibrate the model. Following this calibration step, the level of polymer degradation as a function of flow rate can be predicted for the two other geometries, suggesting that mechanisms linking single molecule scission to macroscopic chemical reaction rate are accurately captured by the model. Although the focus of this work is on flexible linear polymers in dilute concentrations and laminar flow conditions, we discuss how to alleviate these assumptions and extend the applicability of the model to a broader range of materials and industrially relevant flow conditions.

The fluid mechanics of hurricanes strongly depends on boundary layer energetics due to the warm-core nature of the system with peak velocities located at lower levels. One barrier that has inhibited a more complete characterization of energy transfer in the boundary layer is a lack of observations that resolve large, turbulent eddies. In particular, the occurrence and structure of upscale energy transfer (backscatter) in the hurricane boundary layer as well as the effects of backscatter on the vortex intensity are unknown. The analysis presented here of very high-resolution, three-dimensional wind observations from Hurricane Rita (2005) at peak intensity reveals large regions of organized backscatter in the boundary layer associated with coherent, turbulent eddies. Strong forwardscatter is also found next to the backscatter regions due to the interaction between adjacent eddies. Two components of the stress tensor are primarily responsible for this alternating scatter structure, as shown by large correlation coefficients between the fields: the radial–vertical component ($\tau _{13}$) and the azimuthal–vertical component ($\tau _{23}$) with average correlations of 79 % and 49 %, respectively. The Leonard, Reynolds and cross-term stress components are also provided. The impact of the sub-filter-scale energy transfer is estimated by computing the kinetic energy budget for the resolved-scale and eddy-scale motions. The results show that the sub-filter-scale energy transfer term is of the same order as the other terms in the eddy-scale budgets, contributing between 16 % and 40 % to the local time tendency with an average contribution of approximately 30 %. These results indicate that the coherent turbulent eddies can affect the vortex dynamics through wave–wave nonlinear interactions, which can subsequently influence the wave–mean flow interactions. This is the first study to examine the full sub-filter-scale energy transfer and its impact on the kinetic energy budget in the hurricane boundary layer. These findings emphasize the importance of coherent turbulence in the energy cascade and have the potential to improve turbulence closure schemes used in numerical simulations.

We experimentally demonstrate quadrupolar electro-osmotic flows around charged dielectric microspheres immersed in an electrolyte when subjected to an alternating current electric field. We present an electrokinetic model that predicts the flow characteristics based on the phenomena of surface conductance and polarization of the electrolyte concentration around the particles. We refer to these flows as concentration polarization electro-osmosis. We anticipate that these flows may play a major role in the electric-field-induced assembly of colloids and on the electrokinetic manipulation of dielectric micro- and nanoparticles.

We use direct numerical simulations to study the two-dimensional flow of a rotating, half soap bubble that is heated at its equator. The heating produces buoyancy and rotation generates Coriolis forces in the fluid. However, owing to the curved surface of the bubble, the buoyancy and Coriolis forces vary with latitude on the bubble, giving rise to rich flow behaviour. We first explore the single-point properties of the flow, including the Reynolds and Nusselt numbers, mean fields and Reynolds stresses, all as a function of latitude. For a given Rayleigh number, we observe a non-monotonic dependence on the Rossby number $Ro$, and large-scale mean circulations that are strongly influenced by rotation. We then consider quantities that reveal the multiscale nature of the flow, including spectra and spectral fluxes of kinetic and thermal energy, enstrophy and structure functions of velocity and temperature. The fluxes show that just as for non-buoyant two-dimensional turbulence on a flat surface, there is an upscale flux of kinetic energy at larger scales (fed by buoyancy injection of turbulent kinetic energy at smaller scales), and a downscale flux of enstrophy at smaller scales. The kinetic energy spectrum and velocity structure functions are well described by Bolgiano–Obukhov (BO) scaling at scales where the effects of rotation are weak. The temperature structure functions do not, however, satisfy BO scaling in general, owing to strong intermittency in the temperature field.

We propose a semi-analytical solution for the advection–diffusion equation in cylindrical domains, with an aim towards extracting blood flow rates from contrast variations in a coronary computed tomography angiography image. The solution proposed in this work, in contrast with existing methods, which only consider advection, incorporates both radial velocity variation and diffusion. By means of a Galerkin approach using Bessel functions, a solution for a three-dimensional concentration field at a single time point is obtained after a Laplace transformation. This semi-analytical solution forms the basis for a novel advection–diffusion flow estimation (ADFE) method. The ADFE is derived, validated through numerical spectral-element method computations, and shown to exhibit improved accuracy against the state-of-the-art method for image-based blood flow extraction.

To mimic the unsteady vortex–wall interaction of animal propulsion in a canonical test case, a vorticity-annihilating boundary layer was examined through the spin-down of a vortex from solid-body rotation. A cylindrical, water-filled tank was rapidly stopped, and the decay of the vortex from solid-body rotation was observed by means of planar and stereo particle image velocimetry. High Reynolds-number ($Re$) measurements were achieved by combining a large-scale facility (diameter, $D=13\ \textrm {m}$) with a novel approach to reduce end-wall effects. The influence of the boundary-layer formation at the tank's bottom wall was minimised by introducing a saturated salt-water layer. The experimental efforts have allowed us to assess the $Re$ dependency of the laminar–turbulent transition of the vorticity-annihilating side-wall boundary layer at scales similar to large cetaceans. The scaling of the transition mechanism and its onset time were found to agree with predictions from linear stability analysis. Furthermore, the growth rate of the curved turbulent boundary layer was also in good agreement with an empirical scaling formulated in the literature for much smaller $Re$. Eventually, the scaling of vorticity annihilation was addressed. The earlier onset of transition at high $Re$ compensates for the reduced effects of viscosity, leading to similar vorticity annihilation rates during the early stages of the spin-down for a wide $Re$ range.