Research Article
When does an affine curve have an algebraic integer point?
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 1-4
-
- Article
-
- You have access
- Export citation
A Ramsey-type property in additive number theory
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 5-10
-
- Article
-
- You have access
- Export citation
A diophantine equation
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 11-18
-
- Article
-
- You have access
- Export citation
The quadratic reciprocity law and the elementary theta function
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 19-30
-
- Article
-
- You have access
- Export citation
On unramified Am-extensions of quadratic number fields
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 31-37
-
- Article
-
- You have access
- Export citation
Dirichlet and Poincaré series
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 39-56
-
- Article
-
- You have access
- Export citation
Multiplier systems for Hilbert's and Siegel's modular groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 57-80
-
- Article
-
- You have access
- Export citation
Application of a method of Szemeredi
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 81-85
-
- Article
-
- You have access
- Export citation
Small solutions of quadratic congruences
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 87-93
-
- Article
-
- You have access
- Export citation
On the representations of numbers by binary cubic forms
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 95-98
-
- Article
-
- You have access
- Export citation
Character sums and small eigenvalues for Г0(p)
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 99-116
-
- Article
-
- You have access
- Export citation
Diophantine approximation on Hecke groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 117-127
-
- Article
-
- You have access
- Export citation
Generic Dirichlet polygons and the modular group
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 129-141
-
- Article
-
- You have access
- Export citation
The order of magnitude of the mth coefficients of cyclotomic polynomials
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 143-159
-
- Article
-
- You have access
- Export citation
The classical modular group as a subgroup of GL(2, ℤ)†
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 161-164
-
- Article
-
- You have access
- Export citation
The distribution of certain special values of the cubic Legendre symbol
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 165-184
-
- Article
-
- You have access
- Export citation
on l-adic representations attached to modular forms II
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 185-194
-
- Article
-
- You have access
- Export citation
On a theorem of Beck
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 195-201
-
- Article
-
- You have access
- Export citation
Sur la lacunarité des puissances de η
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 203-221
-
- Article
-
- You have access
- Export citation
Represéntations Galoisiennes paires
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 223-237
-
- Article
-
- You have access
- Export citation

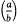 denote the Legendre symbol for relatively prime numbers
denote the Legendre symbol for relatively prime numbers 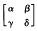 a substitution of the modular subgroup Γ
a substitution of the modular subgroup Γ
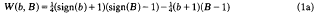
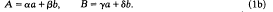
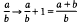 and
and 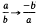 ﹚. (1) follows (see below) from the functional equation
﹚. (1) follows (see below) from the functional equation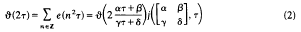
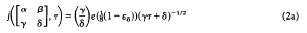
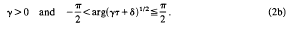
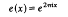
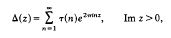
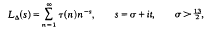
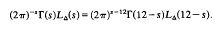

 of
of 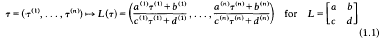
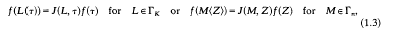
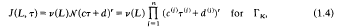



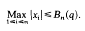
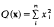 gives the trivial lower bound
gives the trivial lower bound 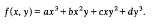
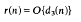
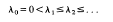
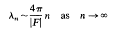



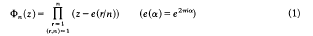

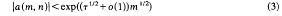
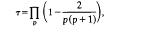
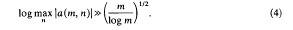
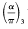 be that third root of unity so that
be that third root of unity so that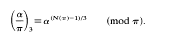
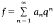 is a newform of weight
is a newform of weight 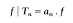
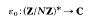
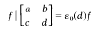
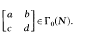 .
.
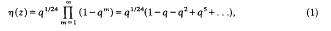
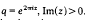 , Im(
, Im(
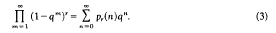
 de dimension 2, de déterminant pair, qui sont de type diédral (I) ou de conducteur premier et de type quelconque (II), en imitant la construction de Tate (Serre [11]) de représentations de déterminant impair.
de dimension 2, de déterminant pair, qui sont de type diédral (I) ou de conducteur premier et de type quelconque (II), en imitant la construction de Tate (Serre [11]) de représentations de déterminant impair.