Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-22T20:35:34.551Z Has data issue: false hasContentIssue false
  • English
  • Français

Dirichlet and Poincaré series

Published online by Cambridge University Press:  18 May 2009

A. Good
A. Good
Affiliation:
School of Mathematics, The Institute for Advanced Study, Princeton NJ 08540
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The study of modular forms has been deeply influenced by famous conjectures and hypotheses concerning

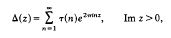
where T(n) denotes Ramanujan's function. The fundamental discriminant Δ is a cusp form of weight 12 with respect to the modular group. Its associated Dirichlet series

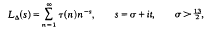
defines an entire function of s and satisfies the functional equation

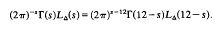
The most penetrating statements that have been made on T(n) and LΔ(s)are:

Of these four problems only A1 has been established so far. This was done by Deligne [1] using methods from algebraic geometry and number theory. While B1 trivially holds with ε > 1/2, it was established in [2] for every ε>1/3. Serre [12] proved A2 for a positive proportion of the integers and Hafner [5] showed that LΔ has a positive proportion of its non-trivial zeros on the line σ=6. The proofs of the last three results are largely analytic in nature.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 27 , October 1985 , pp. 39 - 56
Copyright
Copyright © Glasgow Mathematical Journal Trust 1985

References

REFERENCES

1.Deligne, P., La conjecture de Weil I, Inst. Hautes Études Sci. Publ. Math. 43 (1974), 273–307.CrossRefGoogle Scholar
2.Good, A., The square mean of Dirichlet series associated to cusp forms, Mathematika 29 (1982), 278–295.CrossRefGoogle Scholar
3.Good, A., Cusp forms and eigenfunctions of the Laplacian, Math. Ann. 255 (1981), 523–548.CrossRefGoogle Scholar
4.Good, A., Local analysis of Selberg's trace formula, Lecture Notes in Mathematics 1040 (Springer, 1983).CrossRefGoogle Scholar
5.Hafner, J. L., Zeros on the critical line for Dirichlet series attached to certain cusp forms, Preprint.Google Scholar
6.Knopp, M. I., Modular functions in analytic number theory (Markham, 1970).Google Scholar
7.Kubota, T., Elementary theory of Eisenstein series (Halsted Press, 1973).Google Scholar
8.Magnus, W., Oberhettinger, F. and Soni, R. P., Formulas and theorems for the special functions of mathematical physics, 3rd edition (Springer, 1966).CrossRefGoogle Scholar
9.Ogg, A., Modular forms and Dirichlet series (W. A. Benjamin, 1969).Google Scholar
10.Petersson, H., Theorie der automorphen Formen beliebiger reeller Dimension und ihre Dartellung durch eine neue Art Poincaréscher Reihen, Math. Ann. 103 (1930), 369–436.CrossRefGoogle Scholar
11.Selberg, A., On the estimation of Fourier coefficients of modular forms, Proc. Sympos. Pure Math. VIII (Amer. Math. Soc, 1965), 1–15.Google Scholar
12.Serre, J. -P., Quelques applications du théorème de densité de Chebotarev, Inst. Hautes Études Sci. Publ. Math. 54 (1981), 123–201.CrossRefGoogle Scholar
13.Shimura, G., Introduction to the arithmetic theory of automorphic functions (Princeton University Press, 1971).Google Scholar
14.Zagier, D., Modular forms whose coefficients involve zeta-functions of quadratic fields, Lecture Notes in Mathematics 627 (Springer, 1977), 105–169.Google Scholar