Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-26T07:11:05.085Z Has data issue: false hasContentIssue false
  • English
  • Français

Represéntations Galoisiennes paires

Published online by Cambridge University Press:  18 May 2009

M.-F. Vignéras
M.-F. Vignéras
Affiliation:
École Normale Supérieure, 92120 Montrouge, France
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

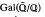On présente des exemples de représentations de de dimension 2, de déterminant pair, qui sont de type diédral (I) ou de conducteur premier et de type quelconque (II), en imitant la construction de Tate (Serre [11]) de représentations de déterminant impair.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 27 , October 1985 , pp. 223 - 237
Copyright
Copyright © Glasgow Mathematical Journal Trust 1985

References

Bibliographie

1.Buhler, J. P., Icosaedral Representations Springer-Verlag Lecture Notes 654 (1978).Google Scholar
2.Borevich, Z. et Chafarevich, I., Théorie des nombres (Gauthiers-Villars, 1967).Google Scholar
3.Borel, A. et Jacquet, H., Automorphic forms and automorphic representations (dans Automorphic Forms, Representations, and L-functions, AMS Proc. of Symp. in Pure Math. vol.XXXIII, part 1, p. 189–202 (1979)).CrossRefGoogle Scholar
4.Casselman, W., GLn dans Algebraic Number Fields, Fröhlich, A. (Academic Press 1977).Google Scholar
5.Casselman, W., On some results of Atkin-Lehner, Math. Ann. 201 (1973), 301–314.CrossRefGoogle Scholar
6.Delone, B. N. et Faddev, D. K., The theory of irrationalities of the third degree Transl. of Math. Mon. vol. 10, AMS (1964).Google Scholar
7.Gelbart, S., Automorphic forms on adeles groups (Ann. of Math. Studies, n° 23, Princeton University Press 1975).CrossRefGoogle Scholar
8.Godwin, H. J., Real quartic fields with small discriminat, J. London Math. Soc. 31 (1956), 478–485.CrossRefGoogle Scholar
9.Li, W., On converse theorems for GL2 and GLi Amer. J. of Math. 103 (1981), 851–885.CrossRefGoogle Scholar
10.Martinet, J., Character Theory and Artin L-functions dans Algebraic Number Fields, Frohlich, A. (Academic Press 1977).Google Scholar
11.Serre, J-P., Modular forms of weight one and Galois representations dans Algebraic Number Fields, Fröhlich, A. (Academic Press 1977).Google Scholar
12.Tunnell, J., Artin's conjecture for representations of octaedral type Bull. Amer. Math. Soc. 5 (1981), 173–175.CrossRefGoogle Scholar