Let 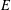 $E$ be an elliptic curve over
$E$ be an elliptic curve over 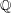 $\mathbb{Q}$, and let
$\mathbb{Q}$, and let 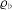 ${\it\varrho}_{\flat }$ and
${\it\varrho}_{\flat }$ and  ${\it\varrho}_{\sharp }$ be odd two-dimensional Artin representations for
which
${\it\varrho}_{\sharp }$ be odd two-dimensional Artin representations for
which 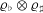 ${\it\varrho}_{\flat }\otimes {\it\varrho}_{\sharp }$ is self-dual. The progress on modularity achieved
in recent decades ensures the existence of normalized eigenforms
${\it\varrho}_{\flat }\otimes {\it\varrho}_{\sharp }$ is self-dual. The progress on modularity achieved
in recent decades ensures the existence of normalized eigenforms 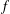 $f$,
$f$, 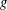 $g$, and
$g$, and 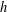 $h$ of respective weights two, one, and one, giving
rise to
$h$ of respective weights two, one, and one, giving
rise to 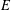 $E$,
$E$, 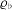 ${\it\varrho}_{\flat }$, and
${\it\varrho}_{\flat }$, and 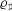 ${\it\varrho}_{\sharp }$ via the constructions of Eichler and Shimura, and
of Deligne and Serre. This article examines certain
${\it\varrho}_{\sharp }$ via the constructions of Eichler and Shimura, and
of Deligne and Serre. This article examines certain 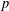 $p$-adic iterated integrals attached
to the triple
$p$-adic iterated integrals attached
to the triple 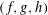 $(f,g,h)$, which are
$(f,g,h)$, which are 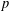 $p$-adic avatars of the leading term of the
Hasse–Weil–Artin
$p$-adic avatars of the leading term of the
Hasse–Weil–Artin 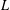 $L$-series
$L$-series 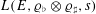 $L(E,{\it\varrho}_{\flat }\otimes {\it\varrho}_{\sharp },s)$ when it has a double zero at the centre. A
formula is proposed for these iterated integrals, involving the formal group
logarithms of global points on
$L(E,{\it\varrho}_{\flat }\otimes {\it\varrho}_{\sharp },s)$ when it has a double zero at the centre. A
formula is proposed for these iterated integrals, involving the formal group
logarithms of global points on  $E$—referred to as Stark
points—which are defined over the number field cut out by
$E$—referred to as Stark
points—which are defined over the number field cut out by 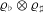 ${\it\varrho}_{\flat }\otimes {\it\varrho}_{\sharp }$. This formula can be viewed as an elliptic curve
analogue of Stark’s conjecture on units attached to weight-one forms. It is
proved when
${\it\varrho}_{\flat }\otimes {\it\varrho}_{\sharp }$. This formula can be viewed as an elliptic curve
analogue of Stark’s conjecture on units attached to weight-one forms. It is
proved when 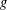 $g$ and
$g$ and 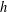 $h$ are binary theta series attached to a common
imaginary quadratic field in which
$h$ are binary theta series attached to a common
imaginary quadratic field in which 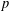 $p$ splits, by relating the arithmetic quantities
that arise in it to elliptic units and Heegner points. Fast algorithms for computing
$p$ splits, by relating the arithmetic quantities
that arise in it to elliptic units and Heegner points. Fast algorithms for computing 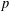 $p$-adic iterated integrals based on Katz expansions
of overconvergent modular forms are then exploited to gather numerical evidence in
more exotic scenarios, encompassing Mordell–Weil groups over cyclotomic
fields, ring class fields of real quadratic fields (a setting which may shed light on
the theory of Stark–Heegner points attached to Shintani-type cycles on
$p$-adic iterated integrals based on Katz expansions
of overconvergent modular forms are then exploited to gather numerical evidence in
more exotic scenarios, encompassing Mordell–Weil groups over cyclotomic
fields, ring class fields of real quadratic fields (a setting which may shed light on
the theory of Stark–Heegner points attached to Shintani-type cycles on 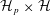 ${\mathcal{H}}_{p}\times {\mathcal{H}}$), and extensions of
${\mathcal{H}}_{p}\times {\mathcal{H}}$), and extensions of 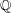 $\mathbb{Q}$ with Galois group a central extension of the
dihedral group
$\mathbb{Q}$ with Galois group a central extension of the
dihedral group 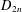 $D_{2n}$ or of one of the exceptional subgroups
$D_{2n}$ or of one of the exceptional subgroups 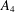 $A_{4}$,
$A_{4}$, 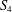 $S_{4}$, and
$S_{4}$, and 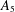 $A_{5}$ of
$A_{5}$ of 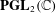 $\mathbf{PGL}_{2}(\mathbb{C})$.
$\mathbf{PGL}_{2}(\mathbb{C})$.
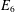 $E_{6}$ AND THE ARITHMETIC OF A FAMILY OF NON-HYPERELLIPTIC CURVES OF GENUS 3
$E_{6}$ AND THE ARITHMETIC OF A FAMILY OF NON-HYPERELLIPTIC CURVES OF GENUS 3
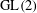 $\text{GL}(2)$
$\text{GL}(2)$
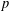 $p$-ADIC ITERATED INTEGRALS ATTACHED TO MODULAR
FORMS OF WEIGHT ONE
$p$-ADIC ITERATED INTEGRALS ATTACHED TO MODULAR
FORMS OF WEIGHT ONE