Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-22T22:31:53.691Z Has data issue: false hasContentIssue false
  • English
  • Français

MODIFIED SCATTERING FOR THE CUBIC SCHRÖDINGER EQUATION ON PRODUCT SPACES AND APPLICATIONS

Part of: Equations of mathematical physics and other areas of application

Published online by Cambridge University Press:  14 August 2015

ZAHER HANI ,
BENOIT PAUSADER ,
NIKOLAY TZVETKOV  and
NICOLA VISCIGLIA
ZAHER HANI
Affiliation:
School of Mathematics, Georgia Institute of Technology, Atlanta, GA 30332, USA; [email protected]
BENOIT PAUSADER
Affiliation:
Université Paris-Nord, France; [email protected]
NIKOLAY TZVETKOV
Affiliation:
Université Cergy-Pontoise, France; [email protected]
NICOLA VISCIGLIA
Affiliation:
Universita di Pisa, Italy; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the cubic nonlinear Schrödinger equation posed on the spatial domain $\mathbb{R}\times \mathbb{T}^{d}$. We prove modified scattering and construct modified wave operators for small initial and final data respectively (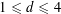$1\leqslant d\leqslant 4$). The key novelty comes from the fact that the modified asymptotic dynamics are dictated by the resonant system of this equation, which sustains interesting dynamics when $d\geqslant 2$. As a consequence, we obtain global strong solutions (for 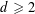$d\geqslant 2$) with infinitely growing high Sobolev norms 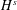$H^{s}$.

MSC classification

Primary: 35Q55: NLS-like equations (nonlinear Schrödinger)
Type
Research Article
Information
Forum of Mathematics, Pi , Volume 3 , 2015 , e4
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2015

References

Alazard, T. and Delort, J. M., ‘Global solutions and asymptotic behavior for two dimensional gravity water waves’, Preprint, 2013, arXiv:1305.4090.CrossRefGoogle Scholar
Antonelli, P., Carles, R. and Silva, J. D., ‘Scattering for nonlinear Schrödinger equation under partial harmonic confinement’, Preprint, 2013, arXiv:1310.1352.CrossRefGoogle Scholar
Banica, V., Carles, R. and Duyckaerts, T., ‘On scattering for NLS: from Euclidean to hyperbolic space’, Discrete Contin. Dyn. Syst. 24(4) (2009), 1113–1127.CrossRefGoogle Scholar
Bourgain, J., ‘Fourier transform restriction phenomena for certain lattice subsets and applications to nonlinear evolution equations. I. Schrödinger equations’, Geom. Funct. Anal. 3 (1993), 107–156.CrossRefGoogle Scholar
Bourgain, J., ‘Exponential sums and nonlinear Schrödinger equations’, Geom. Funct. Anal. 3 (1993), 157–178.CrossRefGoogle Scholar
Bourgain, J., ‘Periodic nonlinear Schrödinger equation and invariant measures’, Comm. Math. Phys. 166 (1994), 1–26.CrossRefGoogle Scholar
Bourgain, J., ‘Aspects of long time behaviour of solutions of nonlinear Hamiltonian evolution equations’, Geom. Funct. Anal. 5(2) (1995), 105–140.CrossRefGoogle Scholar
Bourgain, J., ‘On the growth in time of higher Sobolev norms of smooth solutions of Hamiltonian PDE’, Int. Math. Res. Not. IMRN 6 (1996), 277–304.CrossRefGoogle Scholar
Bourgain, J., ‘Invariant measures for the 2d-defocusing nonlinear Schrödinger equation’, Comm. Math. Phys. 176 (1996), 421–445.CrossRefGoogle Scholar
Bourgain, J., ‘On growth in time of Sobolev norms of smooth solutions of nonlinear Schrödinger equations in ℝD’, J. Anal. Math. 72 (1997), 299–310.CrossRefGoogle Scholar
Bourgain, J., ‘Quasi-periodic solutions of Hamiltonian perturbations of 2D linear Schrödinger equations’, Ann. of Math. (2) 148(2) (1998), 363–439.CrossRefGoogle Scholar
Bourgain, J., ‘Refinements of Strichartz inequality and applications to 2D-NLS with critical nonlinearity’, Int. Math. Res. Not. IMRN (1998), 253–283.CrossRefGoogle Scholar
Bourgain, J., ‘Global wellposedness of defocusing critical nonlinear Schrödinger equation in the radial case’, J. Amer. Math. Soc. 12 (1999), 145–171.CrossRefGoogle Scholar
Bourgain, J., ‘Growth of Sobolev norms in linear Schrödinger equations with quasi-periodic potential’, Comm. Math. Phys. 204(1) (1999), 207–247.CrossRefGoogle Scholar
Bourgain, J., ‘On growth of Sobolev norms in linear Schrödinger equations with smooth, time-dependent potential’, J. Anal. Math. 77 (1999), 315–348.CrossRefGoogle Scholar
Bourgain, J., ‘Problems in Hamiltonian PDE’s’, Geom. Funct. Anal. 2000 (2000), 32–56 (special volume, Part I).Google Scholar
Bourgain, J., ‘Remarks on stability and diffusion in high-dimensional Hamiltonian systems and partial differential equations’, Ergod. Th. & Dynam. Syst. 24(5) (2004), 1331–1357.CrossRefGoogle Scholar
Bourgain, J., ‘Moment inequalities for trigonometric polynomials with spectrum in curved hypersurfaces’, Israel J. Math. 193(1) (2013), 441–458.CrossRefGoogle Scholar
Bourgain, J. and Bulut, A., ‘Almost sure global well posedness for the radial nonlinear Schrödinger equation on the unit ball II: the 3D case’, J. Eur. Math. Soc. 16 (2014), 1289–1325.CrossRefGoogle Scholar
Brézis, H. and Gallouët, T., ‘Nonlinear Schrödinger evolution equations’, Nonlinear Anal. Theory Methods Appl. 4 (1980), 677–681.CrossRefGoogle Scholar
Burq, N., Gérard, P. and Tzvetkov, N., ‘An instability property of the nonlinear Schrödinger equation on Sd’, Math. Res. Lett. 9 (2002), 323–335.CrossRefGoogle Scholar
Burq, N., Gérard, P. and Tzvetkov, N., ‘Strichartz inequalities and the nonlinear Schrödinger equation on compact manifolds’, Amer. J. Math. 126 (2004), 569–605.CrossRefGoogle Scholar
Burq, N., Gérard, P. and Tzvetkov, N., ‘Bilinear eigenfunction estimates and the nonlinear Schrödinger equation on surfaces’, Invent. Math. 159 (2005), 187–223.CrossRefGoogle Scholar
Burq, N., Gérard, P. and Tzvetkov, N., ‘Multilinear eigenfunction estimates and global existence for the three dimensional nonlinear Schrödinger equations’, Ann. Sci. Éc. Norm. Supér. (4) 38 (2005), 255–301.CrossRefGoogle Scholar
Carles, R., ‘Geometric optics and long range scattering for one-dimensional nonlinear Schrödinger equations’, Commun. Math. Phys. 220(1) (2001), 41–67.CrossRefGoogle Scholar
Carles, R. and Faou, E., ‘Energy cascade for NLS on the torus’, Discrete Contin. Dyn. Syst. 32(6) (2012), 2063–2077.CrossRefGoogle Scholar
Cazenave, T., Semilinear Schrödinger Equations, Courant Lecture Notes in Mathematics, 10 (New York University, Courant Institute of Mathematical Sciences, New York; American Mathematical Society, Providence, RI, 2003).CrossRefGoogle Scholar
Colliander, J., Keel, M., Staffilani, G., Takaoka, H. and Tao, T., ‘Global well-posedness for Schrödinger equations with derivative’, SIAM J. Math. Anal. 33 (2001), 649–669.CrossRefGoogle Scholar
Colliander, J., Keel, M., Staffilani, G., Takaoka, H. and Tao, T., ‘Global well-posedness and scattering for the energy-critical nonlinear Schrödinger equation in ℝ3’, Ann. of Math. (2) 167 (2008), 767–865.CrossRefGoogle Scholar
Colliander, J., Keel, M., Staffilani, G., Takaoka, H. and Tao, T., ‘Transfer of energy to high frequencies in the cubic defocusing nonlinear Schrödinger equation’, Invent. Math. 181(1) (2010), 39–113.CrossRefGoogle Scholar
Colliander, J., Kwon, S. and Oh, T., ‘A remark on normal forms and the ‘upside-down’ I-method for periodic NLS: growth of higher Sobolev norms’, J. Anal. Math 118(1) (2012), 55–82.CrossRefGoogle Scholar
Deift, P. and Zhou, X., ‘Long-time asymptotics for solutions of the NLS equation with initial data in a weighted Sobolev space, Dedicated to the memory of Jürgen K. Moser’, Comm. Pure Appl. Math. 56(8) (2003), 1029–1077.CrossRefGoogle Scholar
Delort, J.-M., ‘Existence globale et comportement asymptotique pour l’équation de Klein–Gordon quasi linéaire à données petites en dimension 1’, Ann. Sci. Éc. Norm. Supér. (4) 34(1) (2001), 1–61.CrossRefGoogle Scholar
Dodson, B., ‘Global well-posedness and scattering for the defocusing, $L^{2}$-critical, nonlinear Schrd̈inger equation when $d=1$’, Preprint, 2010, arXiv:1010.0040.Google Scholar
Dodson, B., ‘Global well-posedness and scattering for the defocusing, $L^{2}$-critical, nonlinear Schrödinger equation when $d=2$’, Preprint, 2010, arXiv:1006.1375.Google Scholar
Dodson, B., ‘Global well-posedness and scattering for the defocusing, energy-critical, nonlinear Schrödinger equation in the exterior of a convex obstacle when $d=4$’, Preprint, 2011, arXiv:1112.0710.Google Scholar
Eliasson, L. H. and Kuksin, S., ‘KAM for the nonlinear Schrödinger equation’, Ann. of Math. (2) 172(1) (2010), 371–435.CrossRefGoogle Scholar
Faou, E., Germain, P. and Hani, Z., ‘The weakly nonlinear large box limit of the 2D cubic nonlinear Schrödinger equation’, J. Amer. Math. Soc. (JAMS), to appear, Preprint, 2013, arXiv:1308.6267.Google Scholar
Gérard, P. and Grellier, S., ‘The Szegö cubic equation’, Ann. Sci. Éc. Norm. Supér. (4) 43 (2010), 761–809.CrossRefGoogle Scholar
Gérard, P. and Grellier, S., ‘An explicit formula for the cubic Szegö equation’, Trans. Amer. Math. Soc. 367 (2015), 2979–2995.CrossRefGoogle Scholar
Gérard, P. and Grellier, S., ‘Effective integrable dynamics for some nonlinear wave equation’, Anal. PDE 5 (2012), 1139–1155.CrossRefGoogle Scholar
Germain, P., Masmoudi, N. and Shatah, J., ‘Global solutions for 3D quadratic Schrödinger equations’, Int. Math. Res. Not. IMRN (2009), 414–432.Google Scholar
Germain, P., Masmoudi, N. and Shatah, J., ‘Global solutions for the gravity water waves equation in dimension 3’, Ann. of Math. (2) 175 (2012), 691–754.CrossRefGoogle Scholar
Grebert, B., Paturel, E. and Thomann, L., ‘Beating effects in cubic Schrödinger systems and growth of Sobolev norms’, Nonlinearity 26 (2013), 1361–1376.CrossRefGoogle Scholar
Guardia, M. and Kaloshin, V., ‘Growth of Sobolev norms in the cubic defocusing nonlinear Schrödinger equation’, J. Eur. Math. Soc. 17(1) (2015), 71–149.CrossRefGoogle Scholar
Guardia, M. and Kaloshin, V., ‘Erratum to “Growth of Sobolev norms in the cubic defocusing nonlinear Schrödinger equation”’, personal communication.Google Scholar
Guo, S., ‘On the 1D cubic NLS in an almost critical space’, Master Thesis, University of Bonn (2012).Google Scholar
Guo, Y., Ionescu, A. and Pausader, B., ‘The Euler–Maxwell 2 fluid in $3D$’, Preprint, 2013, arXiv:1303.1060.Google Scholar
Hani, Z., ‘Global well-posedness of the cubic nonlinear Schrödinger equation on compact manifolds without boundary’, Comm. Partial Differential Equations 37(7) (2012), 1186–1236.CrossRefGoogle Scholar
Hani, Z., ‘Long-time strong instability and unbounded orbits for some periodic nonlinear Schödinger equations’, Arch. Ration. Mech. Anal. 211(3) (2014), 929–964.CrossRefGoogle Scholar
Hani, Z. and Pausader, B., ‘On scattering for the quintic defocusing nonlinear Schrödinger equation on ℝ ×T2’, Comm. Pure Appl. Math. 67(9) (2014), 1466–1542.CrossRefGoogle Scholar
Hani, Z. and Thomann, L., ‘Asymptotic behavior of the nonlinear Schrödinger equation with harmonic trapping’, Commun. Pure Appl. Math. (CPAM) Preprint, 2014, arXiv:1408.6213, published online: 15 July 2015, doi:10.1002/cpa.21594.CrossRefGoogle Scholar
Hayashi, N., Li, C. and Naumkin, P., ‘Modified wave operator for a system of nonlinear Schrödinger equations in 2d’, Comm. Partial Differential Equations 37(6) (2012), 947–968.CrossRefGoogle Scholar
Hayashi, N. and Naumkin, P., ‘Asymptotics for large time of solutions to the nonlinear Schrödinger and Hartree equations’, Amer. J. Math. 120(2) (1998), 369–389.CrossRefGoogle Scholar
Hayashi, N., Naumkin, P., Shimomura, A. and Tonegawa, S., ‘Modified wave operators for nonlinear Schrödinger equations in one and two dimensions’, Electron. J. Differential Equations 62 (2004), 16 pp.Google Scholar
Herr, S., ‘The quintic nonlinear Schrödinger equation on three-dimensional Zoll manifolds’, Amer. J. Math. 135(5) (2013), 1271–1290.CrossRefGoogle Scholar
Herr, S., Tataru, D. and Tzvetkov, N., ‘Global well-posedness of the energy critical nonlinear Schrödinger equation with small initial data in H 1(T3)’, Duke Math. J. 159 (2011), 329–349.CrossRefGoogle Scholar
Herr, S., Tataru, D. and Tzvetkov, N., ‘Strichartz estimates for partially periodic solutions to Schrödinger equations in 4d and applications’, J. Ang. Math. 2014(690) (2012), 65–78.Google Scholar
Ionescu, A. D. and Pausader, B., ‘Global wellposedness of the energy-critical defocusing NLS on ℝ ×T3’, Commun. Math. Phys. 312(3) (2012), 781–831.CrossRefGoogle Scholar
Ionescu, A. D. and Pausader, B., ‘The energy-critical defocusing NLS on T3’, Duke Math. J. 161(8) (2012), 1581–1612.CrossRefGoogle Scholar
Ionescu, A. D., Pausader, B. and Staffilani, G., ‘On the global well-posedness of energy-critical Schrödinger equations in curved spaces’, Anal. PDE 5(4) (2012), 705–746.CrossRefGoogle Scholar
Ionescu, A. and Pausader, B., ‘Global solutions of quasilinear systems of Klein–Gordon equations in 3D’, J. Eur. Math. Soc. 16(11) (2014), 2355–2431.CrossRefGoogle Scholar
Ionescu, A. D. and Pusateri, F., ‘Nonlinear fractional Schrödinger equations in one dimensions’, J. Funct. Anal. 266(1) (2014), 139–176.CrossRefGoogle Scholar
Ionescu, A. D. and Pusateri, F., ‘Global solutions for the gravity water waves system in 2d’, Invent. Math. 199(3) (2015), 653–804.CrossRefGoogle Scholar
Ionescu, A. D. and Staffilani, G., ‘Semilinear Schrödinger flows on hyperbolic spaces: scattering in H 1’, Math. Ann. 345 (2009), 133–158.CrossRefGoogle Scholar
Kato, J. and Pusateri, F., ‘A new proof of long range scattering for critical nonlinear Schrödinger equations’, J. Diff. Int. Equ. 24(9–10) (2011).Google Scholar
Kenig, C. E. and Merle, F., ‘Global well-posedness, scattering and blow-up for the energy-critical, focusing, nonlinear Schrödinger equation in the radial case’, Invent. Math. 166 (2006), 645–675.CrossRefGoogle Scholar
Killip, R., Tao, T. and Visan, M., ‘The cubic nonlinear Schrödinger equation in two dimensions with radial data’, J. Eur. Math. Soc. 11 (2009), 1203–1258.CrossRefGoogle Scholar
Killip, R. and Visan, M., ‘Global well-posedness and scattering for the defocusing quintic NLS in three dimensions’, Anal. PDE 5 (2012), 855–885.CrossRefGoogle Scholar
Killip, R., Visan, M. and Zhang, X., ‘Quintic NLS in the exterior of a strictly convex obstacle’, Preprint, 2012, arXiv:1208.4904.Google Scholar
Kuksin, S., ‘Oscillations in space-periodic nonlinear Schrödinger equations’, Geom. Funct. Anal. 7(2) (1997), 338–363.CrossRefGoogle Scholar
Kuksin, S. and Pöschel, J., ‘Invariant Cantor manifolds of quasi periodic oscillations for a nonlinear Schrödinger equation’, Ann. of Math. (2) 143 (1996), 149–179.CrossRefGoogle Scholar
Majda, A., McLaughlin, D. and Tabak, E., ‘A one-dimensional model for dispersive wave turbulence’, J. Nonlinear Sci. 7(1) (1997), 9–44.CrossRefGoogle Scholar
Ozawa, T., ‘Long range scattering for nonlinear Schrödinger equations in one space dimension’, Commun. Math. Phys. 139 (1991), 479–493.CrossRefGoogle Scholar
Pausader, B., Tzvetkov, N. and Wang, X., ‘Global regularity for the energy-critical NLS on S3’, Ann. Inst. H. Poincaré Anal. Non Linéaire 31(2) (2014), 315–338.Google Scholar
Pocovnicu, O., ‘Explicit formula for the solution of the Szegö equation on the real line and applications’, Discrete Contin. Dyn. Syst. 31 (2011), 607–649.CrossRefGoogle Scholar
Pocovnicu, O., ‘First and second order approximations for a nonlinear wave equation’, J. Dynam. Differential Equations 25(2) (2013), 305–333. 29.CrossRefGoogle Scholar
Procesi, M. and Procesi, C., ‘A KAM algorithm for the resonant nonlinear Schrödinger equation’, Preprint arXiv:1211.4242.Google Scholar
Ryckman, E. and Visan, M., ‘Global well-posedness and scattering for the defocusing energy-critical nonlinear Schrödinger equation in ℝ1+4’, Amer. J. Math. 129 (2007), 1–60.CrossRefGoogle Scholar
Sohinger, V., ‘Bounds on the growth of high Sobolev norms of solutions to nonlinear Schrödinger equations on S 1’, Differential Integral Equations 24(7–8) (2011), 653–718.CrossRefGoogle Scholar
Staffilani, G., ‘On the growth of high Sobolev norms of solutions for KdV and Schrödinger equations’, Duke Math. J. 86(1) (1997), 109–142.CrossRefGoogle Scholar
Takaoka, H. and Tzvetkov, N., ‘On 2D Nonlinear Schrödinger equations with data on ℝ×T’, J. Funct. Anal. 182 (2001), 427–442.CrossRefGoogle Scholar
Terracini, S., Tzvetkov, N. and Visciglia, N., ‘The NLS ground states on product spaces’, Anal. PDE 7(1) (2014), 73–96.CrossRefGoogle Scholar
Tzvetkov, N., ‘Invariant measures for the defocusing NLS’, Ann. Inst. Fourier 58 (2008), 2543–2604.CrossRefGoogle Scholar
Tzvetkov, N. and Visciglia, N., ‘Small data scattering for the nonlinear Schrödinger equation on product spaces’, Comm. Partial Differential Equations 37(1) (2012), 125–135.CrossRefGoogle Scholar
Tzvetkov, N. and Visciglia, N., ‘Well-posedness and scattering for NLS on $\mathbb{R}^{d}\times \mathbb{T}$ in the energy space’, Preprint, 2014, arXiv:1409.3938.Google Scholar
Visan, M., ‘Global well-posedness and scattering for the defocusing cubic NLS in four dimensions’, Int. Math. Res. Not. IMRN 2011 (2011), doi:10.1093/imrn/rnr051.Google Scholar
Xu, H., ‘Large time blow up for a perturbation of the cubic Szegö equation’, Preprint, 2013, arXiv:1307.5284.Google Scholar
Zakharov, V. E. and Shabat, A. B., ‘Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media’, Sov. Phys. JEPT 34 (1972), 62–69.Google Scholar
Zakharov, V. E., L’vov, V. and Falkovich, G., Kolmogorov Spectra of Turbulence 1. Wave Turbulence, Springer Series in Nonlinear Dynamics, (Springer, Berlin, Heidelberg, 1992).CrossRefGoogle Scholar