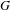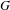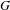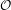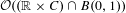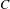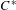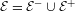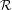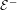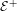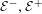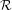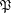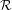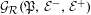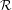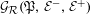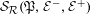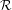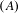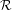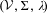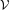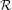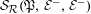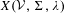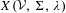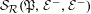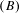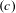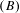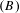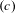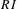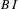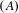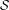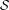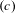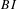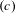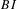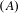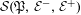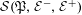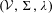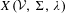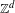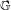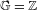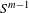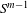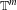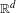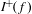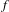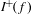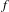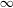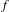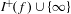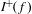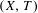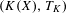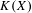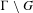We consider partitioned graphs, by which we mean finite directed graphs with a partitioned edge set 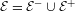 ${\mathcal{E}}={\mathcal{E}}^{-}\cup {\mathcal{E}}^{+}$. Additionally given a relation
${\mathcal{E}}={\mathcal{E}}^{-}\cup {\mathcal{E}}^{+}$. Additionally given a relation 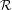 ${\mathcal{R}}$ between the edges in
${\mathcal{R}}$ between the edges in 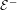 ${\mathcal{E}}^{-}$ and the edges in
${\mathcal{E}}^{-}$ and the edges in 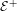 ${\mathcal{E}}^{+}$, and under the appropriate assumptions on
${\mathcal{E}}^{+}$, and under the appropriate assumptions on 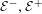 ${\mathcal{E}}^{-},{\mathcal{E}}^{+}$ and
${\mathcal{E}}^{-},{\mathcal{E}}^{+}$ and 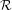 ${\mathcal{R}}$, denoting the vertex set of the graph by
${\mathcal{R}}$, denoting the vertex set of the graph by 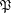 $\mathfrak{P}$, we speak of an
$\mathfrak{P}$, we speak of an 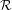 ${\mathcal{R}}$-graph
${\mathcal{R}}$-graph 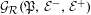 ${\mathcal{G}}_{{\mathcal{R}}}(\mathfrak{P},{\mathcal{E}}^{-},{\mathcal{E}}^{+})$. From
${\mathcal{G}}_{{\mathcal{R}}}(\mathfrak{P},{\mathcal{E}}^{-},{\mathcal{E}}^{+})$. From 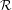 ${\mathcal{R}}$-graphs
${\mathcal{R}}$-graphs 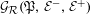 ${\mathcal{G}}_{{\mathcal{R}}}(\mathfrak{P},{\mathcal{E}}^{-},{\mathcal{E}}^{+})$ we construct semigroups (with zero)
${\mathcal{G}}_{{\mathcal{R}}}(\mathfrak{P},{\mathcal{E}}^{-},{\mathcal{E}}^{+})$ we construct semigroups (with zero) 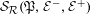 ${\mathcal{S}}_{{\mathcal{R}}}(\mathfrak{P},{\mathcal{E}}^{-},{\mathcal{E}}^{+})$ that we call
${\mathcal{S}}_{{\mathcal{R}}}(\mathfrak{P},{\mathcal{E}}^{-},{\mathcal{E}}^{+})$ that we call 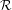 ${\mathcal{R}}$-graph semigroups. We write a list of conditions on a topologically transitive subshift with property
${\mathcal{R}}$-graph semigroups. We write a list of conditions on a topologically transitive subshift with property 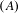 $(A)$ that together are sufficient for the subshift to have an
$(A)$ that together are sufficient for the subshift to have an 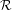 ${\mathcal{R}}$-graph semigroup as its associated semigroup.
${\mathcal{R}}$-graph semigroup as its associated semigroup.
Generalizing previous constructions, we describe a method of presenting subshifts by means of suitably structured finite labeled directed graphs 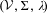 $({\mathcal{V}},~\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D706}~)$ with vertex set
$({\mathcal{V}},~\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D706}~)$ with vertex set 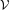 ${\mathcal{V}}$, edge set
${\mathcal{V}}$, edge set  $\unicode[STIX]{x1D6F4}$, and a label map that assigns to the edges in
$\unicode[STIX]{x1D6F4}$, and a label map that assigns to the edges in  $\unicode[STIX]{x1D6F4}$ labels in an
$\unicode[STIX]{x1D6F4}$ labels in an 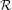 ${\mathcal{R}}$-graph semigroup
${\mathcal{R}}$-graph semigroup 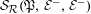 ${\mathcal{S}}_{{\mathcal{R}}}(\mathfrak{P},{\mathcal{E}}^{-},{\mathcal{E}}^{-})$. We denote the presented subshift by
${\mathcal{S}}_{{\mathcal{R}}}(\mathfrak{P},{\mathcal{E}}^{-},{\mathcal{E}}^{-})$. We denote the presented subshift by 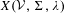 $X({\mathcal{V}},\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D706})$ and call
$X({\mathcal{V}},\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D706})$ and call 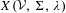 $X({\mathcal{V}},\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D706})$ an
$X({\mathcal{V}},\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D706})$ an 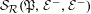 ${\mathcal{S}}_{{\mathcal{R}}}(\mathfrak{P},{\mathcal{E}}^{-},{\mathcal{E}}^{-})$-presentation.
${\mathcal{S}}_{{\mathcal{R}}}(\mathfrak{P},{\mathcal{E}}^{-},{\mathcal{E}}^{-})$-presentation.
We introduce a property 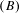 $(B)$ of subshifts that describes a relationship between contexts of admissible words of a subshift, and we introduce a property
$(B)$ of subshifts that describes a relationship between contexts of admissible words of a subshift, and we introduce a property 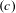 $(c)$ of subshifts that in addition describes a relationship between the past and future contexts and the context of admissible words of a subshift. Property
$(c)$ of subshifts that in addition describes a relationship between the past and future contexts and the context of admissible words of a subshift. Property 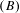 $(B)$ and the simultaneous occurrence of properties
$(B)$ and the simultaneous occurrence of properties 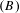 $(B)$ and
$(B)$ and 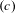 $(c)$ are invariants of topological conjugacy.
$(c)$ are invariants of topological conjugacy.
We consider subshifts in which every admissible word has a future context that is compatible with its entire past context. Such subshifts we call right instantaneous. We introduce a property 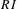 $RI$ of subshifts, and we prove that this property is a necessary and sufficient condition for a subshift to have a right instantaneous presentation. We consider also subshifts in which every admissible word has a future context that is compatible with its entire past context, and also a past context that is compatible with its entire future context. Such subshifts we call bi-instantaneous. We introduce a property
$RI$ of subshifts, and we prove that this property is a necessary and sufficient condition for a subshift to have a right instantaneous presentation. We consider also subshifts in which every admissible word has a future context that is compatible with its entire past context, and also a past context that is compatible with its entire future context. Such subshifts we call bi-instantaneous. We introduce a property 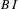 $BI$ of subshifts, and we prove that this property is a necessary and sufficient condition for a subshift to have a bi-instantaneous presentation.
$BI$ of subshifts, and we prove that this property is a necessary and sufficient condition for a subshift to have a bi-instantaneous presentation.
We define a subshift as strongly bi-instantaneous if it has for every sufficiently long admissible word  $a$ an admissible word
$a$ an admissible word  $c$, that is contained in both the future context of
$c$, that is contained in both the future context of  $a$ and the past context of
$a$ and the past context of  $a$, and that is such that the word
$a$, and that is such that the word 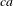 $ca$ is a word in the future context of
$ca$ is a word in the future context of  $a$ that is compatible with the entire past context of
$a$ that is compatible with the entire past context of  $a$, and the word
$a$, and the word 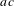 $ac$ is a word in the past context of
$ac$ is a word in the past context of  $a$, that is compatible with the entire future context of
$a$, that is compatible with the entire future context of  $a$. We show that a topologically transitive subshift with property
$a$. We show that a topologically transitive subshift with property 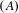 $(A)$, and associated semigroup a graph inverse semigroup
$(A)$, and associated semigroup a graph inverse semigroup 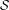 ${\mathcal{S}}$, has an
${\mathcal{S}}$, has an 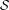 ${\mathcal{S}}$-presentation, if and only if it has properties
${\mathcal{S}}$-presentation, if and only if it has properties 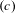 $(c)$ and
$(c)$ and 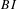 $BI$, and a strongly bi-instantaneous presentation, if and only if it has properties
$BI$, and a strongly bi-instantaneous presentation, if and only if it has properties 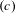 $(c)$ and
$(c)$ and 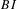 $BI$, and all of its bi-instantaneous presentations are strongly bi-instantaneous.
$BI$, and all of its bi-instantaneous presentations are strongly bi-instantaneous.
We construct a class of subshifts with property 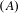 $(A)$, to which certain graph inverse semigroups
$(A)$, to which certain graph inverse semigroups 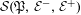 ${\mathcal{S}}(\mathfrak{P},{\mathcal{E}}^{-},{\mathcal{E}}^{+})$ are associated, that do not have
${\mathcal{S}}(\mathfrak{P},{\mathcal{E}}^{-},{\mathcal{E}}^{+})$ are associated, that do not have 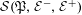 ${\mathcal{S}}(\mathfrak{P},{\mathcal{E}}^{-},{\mathcal{E}}^{+})$-presentations.
${\mathcal{S}}(\mathfrak{P},{\mathcal{E}}^{-},{\mathcal{E}}^{+})$-presentations.
We associate to the labeled directed graphs 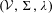 $({\mathcal{V}},\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D706})$ topological Markov chains and Markov codes, and we derive an expression for the zeta function of
$({\mathcal{V}},\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D706})$ topological Markov chains and Markov codes, and we derive an expression for the zeta function of 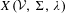 $X({\mathcal{V}},\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D706})$ in terms of the zeta functions of the topological Markov shifts and the generating functions of the Markov codes.
$X({\mathcal{V}},\unicode[STIX]{x1D6F4},\unicode[STIX]{x1D706})$ in terms of the zeta functions of the topological Markov shifts and the generating functions of the Markov codes.
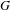 $G$-measures
$G$-measures