Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T00:33:00.241Z Has data issue: false hasContentIssue false
  • English
  • Français

Irrational rotation factors for conservative torus homeomorphisms

Published online by Cambridge University Press:  08 March 2016

T. JÄGER  and
F. TAL
T. JÄGER
Affiliation:
Institute of Mathematics, FSU Jena, Germany email [email protected]
F. TAL
Affiliation:
Universidade de São Paulo, Brasil email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We provide an equivalent characterization for the existence of one-dimensional irrational rotation factors of conservative torus homeomorphisms that are not eventually annular. It states that an area-preserving non-annular torus homeomorphism 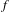$f$ is semiconjugate to an irrational rotation $R_{\unicode[STIX]{x1D6FC}}$ of the circle if and only if there exists a well-defined speed of rotation in some rational direction on the torus, and the deviations from the constant rotation in this direction are uniformly bounded. By means of a counterexample, we also demonstrate that a similar characterization does not hold for eventually annular torus homeomorphisms.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 5 , August 2017 , pp. 1537 - 1546
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Poincaré, H.. Mémoire sur les courbes définies par une équation différentielle. J. Math. Pures Appl., Série IV 1 (1885), 167–244.Google Scholar
Denjoy, A.. Sur les courbes définies par les équations différentielles à la surface du tore. J. Math. Pures Appl. 11 (1932), 333–376.Google Scholar
Jäger, T. and Stark, J.. Towards a classification for quasiperiodically forced circle homeomorphisms. J. Lond. Math. Soc. 73(3) (2006), 727–744.Google Scholar
Aliste-Prieto, J.. Translation numbers for a class of maps on the dynamical systems arising from quasicrystals in the real line. Ergod. Th. & Dynam. Sys. 30(02) (2010), 565–594.CrossRefGoogle Scholar
Aliste-Prieto, J. and Jäger, T.. Almost periodic structures and the semiconjugacy problem. J. Differential Equations 252(9) (2012), 4988–5001.CrossRefGoogle Scholar
Jäger, T.. Linearisation of conservative toral homeomorphisms. Invent. Math. 176(3) (2009), 601–616.CrossRefGoogle Scholar
Jäger, T. and Koropecki, A.. Poincaré theory for decomposable cofrontiers. E-print arXiv:1506.01096.Google Scholar
Franks, J. and Le Calvez, P.. Regions of instability for non-twist maps. Ergod. Th. & Dynam. Sys. 23(1) (2003), 111–141.CrossRefGoogle Scholar
Béguin, F., Crovisier, S. and Le Roux, F.. Pseudo-rotations of the closed annulus: variation on a theorem of J. Kwapisz. Nonlinearity 17(4) (2004), 1427–1453.Google Scholar
Jäger, T.. Periodic point free homeomorphisms of the open annulus – from skew products to non-fibred maps. Proc. Amer. Math. Soc. 138 (2010), 1751–1764.Google Scholar
Misiurewicz, M. and Ziemian, K.. Rotation sets for maps of tori. J. Lond. Math. Soc. 40 (1989), 490–506.Google Scholar
Koropecki, Andres and Tal, Fabio Armando. Strictly toral dynamics. Invent. Math. 196(2) (2014), 339–381.Google Scholar
Jäger, T.. The concept of bounded mean motion for toral homeomorphisms. Dyn. Syst. 24(3) (2009), 277–297.CrossRefGoogle Scholar
Guelman, N., Koropecki, A. and Armando Tal, F.. Rotation sets with non-empty interior and transitivity in the universal covering. Ergod. Th. & Dynam. Sys. 35 (2015), 883–894.CrossRefGoogle Scholar
Besicovitch, A. S.. A problem on topological transformations of the plane. II. Math. Proc. Cambridge Philos. Soc. 47 (1951), 38–45.CrossRefGoogle Scholar
Shnirelman, L. G.. An example of a transformation of the plane. Proc. Don Polytechnic Inst. (Novochekassk) 14 (1930), 64–74 (Science section, Fis-math. part).Google Scholar