Hostname: page-component-669899f699-7xsfk Total loading time: 0 Render date: 2025-05-04T05:45:43.445Z Has data issue: false hasContentIssue false
  • English
  • Français

Connectedness properties of the set where the iterates of an entire function are unbounded

Published online by Cambridge University Press:  23 March 2016

J. W. OSBORNE ,
P. J. RIPPON  and
G. M. STALLARD
J. W. OSBORNE
Affiliation:
Department of Mathematics and Statistics, The Open University, Walton Hall, Milton Keynes, MK7 6AA, UK email [email protected], [email protected], [email protected]
P. J. RIPPON
Affiliation:
Department of Mathematics and Statistics, The Open University, Walton Hall, Milton Keynes, MK7 6AA, UK email [email protected], [email protected], [email protected]
G. M. STALLARD
Affiliation:
Department of Mathematics and Statistics, The Open University, Walton Hall, Milton Keynes, MK7 6AA, UK email [email protected], [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the connectedness properties of the set 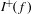$I^{\!+\!}(f)$ of points where the iterates of an entire function 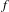$f$ are unbounded. In particular, we show that 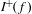$I^{\!+\!}(f)$ is connected whenever iterates of the minimum modulus of 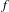$f$ tend to 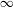$\infty$. For a general transcendental entire function 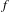$f$, we show that 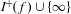$I^{\!+\!}(f)\cup \{\infty \}$ is always connected and that, if 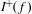$I^{\!+\!}(f)$ is disconnected, then it has uncountably many components, infinitely many of which are unbounded.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 4 , June 2017 , pp. 1291 - 1307
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Baker, I. N.. Repulsive fixpoints of entire functions. Math. Z. 104 (1968), 252–256.CrossRefGoogle Scholar
Baker, I. N.. Wandering domains in the iteration of entire functions. Proc. Lond. Math. Soc. (3) 49 (1984), 563–576.Google Scholar
Baker, I. N. and Domínguez, P.. Boundaries of unbounded Fatou components of entire functions. Ann. Acad. Sci. Fenn. Math. 24 (1999), 437–464.Google Scholar
Beardon, A. F.. Iteration of Rational Functions (Graduate Texts in Mathematics, 132) . Springer, New York, 1991.Google Scholar
Bergweiler, W.. Iteration of meromorphic functions. Bull. Amer. Math. Soc. 29 (1993), 151–188.Google Scholar
Bergweiler, W. and Hinkkanen, A.. On semiconjugation of entire functions. Math. Proc. Cambridge Philos. Soc. 126 (1999), 565–574.Google Scholar
Eremenko, A. E.. On the iteration of entire functions. Dynamical Systems and Ergodic Theory (Banach Center Publications, 23) . Polish Scientific, Warsaw, 1989, pp. 339–345.Google Scholar
Milnor, J.. Dynamics in One Complex Variable, 3rd edn. Princeton University Press, Princeton, NJ, 2006.Google Scholar
Newman, M. H. A.. Elements of the Topology of Plane Sets of Points. Cambridge University Press, New York, reprinted 2008.Google Scholar
Osborne, J.. Connectedness properties of the set where the iterates of an entire function are bounded. Math. Proc. Cambridge Philos. Soc. 155(3) (2013), 391–410.Google Scholar
Osborne, J. W. and Sixsmith, D. J.. On the set where the iterates of an entire function are neither escaping nor bounded. Ann. Acad. Sci. Fenn. Math., to appear. Preprint, 2015, arXiv:1503.08077.Google Scholar
Rempe, L.. On a question of Eremenko concerning escaping components of entire functions. Bull. Lond. Math. Soc. 39(4) (2007), 661–666.Google Scholar
Rempe, L.. Connected escaping sets of exponential maps. Ann. Acad. Sci. Fenn. Math. 36 (2011), 71–80.Google Scholar
Rippon, P. J. and Stallard, G. M.. On questions of Fatou and Eremenko. Proc. Amer. Math. Soc. 133 (2005), 1119–1126.Google Scholar
Rippon, P. J. and Stallard, G. M.. Slow escaping points of meromorphic functions. Trans. Amer. Math. Soc. 363(8) (2011), 4171–4201.Google Scholar
Rippon, P. J. and Stallard, G. M.. Boundaries of escaping Fatou components. Proc. Amer. Math. Soc. 139(8) (2011), 2807–2820.Google Scholar
Rippon, P. J. and Stallard, G. M.. Fast escaping points of entire functions. Proc. Lond. Math. Soc. 105(4) (2012), 787–820.Google Scholar
Rippon, P. J. and Stallard, G. M.. Boundaries of univalent Baker domains. J. Anal., to appear, arXiv:1411.6999.Google Scholar
Rottenfußer, G., Rückert, J., Rempe, L. and Schleicher, D.. Dynamic rays of bounded-type entire functions. Ann. of Math. (2) 173(1) (2011), 77–125.Google Scholar
Sixsmith, D. J.. Maximally and non-maximally fast escaping points of transcendental entire functions. Math. Proc. Cambridge Philos. Soc. 158(2) (2015), 365–383.Google Scholar