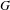Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T00:34:21.040Z Has data issue: false hasContentIssue false
  • English
  • Français

The critical dimension for $G$-measures

Published online by Cambridge University Press:  21 October 2015

DANIEL F. MANSFIELD  and
ANTHONY H. DOOLEY
DANIEL F. MANSFIELD
Affiliation:
School of Mathematics and Statistics, University of New South Wales, Sydney, Australia email [email protected]
ANTHONY H. DOOLEY
Affiliation:
Department of Mathematical Sciences, University of Bath, Bath, UK email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The critical dimension of an ergodic non-singular dynamical system is the asymptotic growth rate of sums of consecutive Radon–Nikodým derivatives. This has been shown to equal the average coordinate entropy for product odometers when the size of individual factors is bounded. We extend this result to 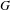$G$-measures with an asymptotic bound on the size of individual factors. Furthermore, unlike von Neumann–Krieger type, the critical dimension is an invariant property on the class of ergodic 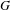$G$-measures.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 3 , May 2017 , pp. 824 - 836
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Brown, G. and Dooley, A. H.. Ergodic measures are of weak product type. Math. Proc. Cambridge Philos. Soc. 98 (1985), 129–145.Google Scholar
Brown, G. and Dooley, A. H.. Odometer actions on G-mesaures. Ergod. Th. & Dynam. Sys. 11 (1991), 297–307.Google Scholar
Dooley, A. H. and Hagihara, R.. Computing the critical dimension of Bratteli–Vershik systems with multiple edges. Ergod. Th. & Dynam. Sys. 32 (2011), 103–117.Google Scholar
Dooley, A. H. and Hamachi, T.. Nonsingular dynamical systems, Bratteli diagrams and Markov odometers. Israel J. Math. 138 (2003), 93–123.CrossRefGoogle Scholar
Dooley, A. H. and Mortiss, G.. On the critical dimension of product odometers. Ergod. Th. & Dynam. Sys. 29 (2009), 475–485.Google Scholar
Dooley, A. H. and Rudolph, D.. Non-uniqueness in G-measures. Ergod. Th. & Dynam. Sys. 32 (2011), 575–586.Google Scholar
Dooley, A. H. and Stenflo, Ö.. A criterion for uniqueness in G-measures and perfect sampling. Math. Proc. Cambridge Philos. Soc. 140 (2006), 545–551.CrossRefGoogle Scholar
Herman, R. H., Putnam, I. F. and Skau, C. F.. Ordered Bratteli diagrams, dimension groups and topological dynamics. Internat. J. Math. 3(6) (1992), 827–864.Google Scholar
Keane, M.. Strongly mixing g-measures. Invent. Math. 16 (1972), 309–324.Google Scholar
Mortiss, G.. Average co-ordinate entropy. J. Aust. Math. Soc. 73 (2002), 171–186.Google Scholar
Mortiss, G.. An invariant for non-singular isomorphism. Ergod. Th. & Dynam. Sys. 23 (2003), 885–893.Google Scholar
Rauzy, G.. Propriétés statistiques de suites arithmétiques. Presses Universitaires de France, Paris, 1976.Google Scholar