Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T00:57:34.770Z Has data issue: false hasContentIssue false
  • English
  • Français

Direct topological factorization for topological flows

Published online by Cambridge University Press:  27 November 2015

TOM MEYEROVITCH
TOM MEYEROVITCH*
Affiliation:
Department of Mathematics, Ben-Gurion University of the Negev, Israel email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper considers the general question of when a topological action of a countable group can be factored into a direct product of non-trivial actions. In the early 1980s, D. Lind considered such questions for $\mathbb{Z}$-shifts of finite type. In particular, we study direct factorizations of subshifts of finite type over 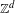$\mathbb{Z}^{d}$ and other groups, and $\mathbb{Z}$-subshifts which are not of finite type. The main results concern direct factors of the multidimensional full $n$-shift, the multidimensional $3$-colored chessboard and the Dyck shift over a prime alphabet. A direct factorization of an expansive 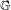$\mathbb{G}$-action must be finite, but an example is provided of a non-expansive $\mathbb{Z}$-action for which there is no finite direct-prime factorization. The question about existence of direct-prime factorization of expansive actions remains open, even for 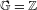$\mathbb{G}=\mathbb{Z}$.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 3 , May 2017 , pp. 837 - 858
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Blanchard, F.. Fully positive topological entropy and topological mixing. Symbolic Dynamics and its Applications (New Haven, CT, 1991) (Contemporary Mathematics, 135) . American Mathematical Society, Providence, RI, 1992, pp. 95–105.Google Scholar
Blanchard, F. and Hansel, G.. Systèmes codés. Theoret. Comput. Sci. 44(1) (1986), 17–49.CrossRefGoogle Scholar
Bowen, R.. Topological entropy and axiom A. Global Analysis (Proceedings of Symposia in Pure Mathematics, XIV, Berkeley, CA, 1968). American Mathematical Society, Providence, RI, 1970, pp. 23–41.Google Scholar
Boyle, M., Marcus, B. and Trow, P.. Resolving maps and the dimension group for shifts of finite type. Mem. Amer. Math. Soc. 70(377) (1987), vi+146.Google Scholar
Boyle, M., Pavlov, R. and Schraudner, M.. Multidimensional sofic shifts without separation and their factors. Trans. Amer. Math. Soc. 362(9) (2010), 4617–4653.CrossRefGoogle Scholar
Chandgotia, N. and Meyerovitch, T.. Markov random fields, Markov cocycles and the 3-colored chessboard. Preprint, 2013, arXiv:1305.0808.Google Scholar
Chung, N.-P. and Li, H.. Homoclinic groups, i.e. groups, and expansive algebraic actions. Invent. Math. 199(3) (2015), 805–858.Google Scholar
Furstenberg, H.. Disjointness in ergodic theory, minimal sets, and a problem in Diophantine approximation. Math. Syst. Theory 1 (1967), 1–49.Google Scholar
Glasner, E.. Ergodic Theory via Joinings (Mathematical Surveys and Monographs, 101) . American Mathematical Society, Providence, RI, 2003.Google Scholar
Hamachi, T., Inoue, K. and Krieger, W.. Subsystems of finite type and semigroup invariants of subshifts. J. Reine Angew. Math. 632 (2009), 37–61.Google Scholar
Hochman, M. and Meyerovitch, T.. A characterization of the entropies of multidimensional shifts of finite type. Ann. of Math. (2) 171(3) (2010), 2011–2038.Google Scholar
Kari, J.. Representation of reversible cellular automata with block permutations. Math. Syst. Theory 29(1) (1996), 47–61.Google Scholar
Krieger, W.. On the uniqueness of the equilibrium state. Math. Syst. Theory 8(2) (1974/75), 97–104.CrossRefGoogle Scholar
Krieger, W.. On a syntactically defined invariant of symbolic dynamics. Ergod. Th. & Dynam. Sys. 20(2) (2000), 501–516.Google Scholar
Krieger, W. and Matsumoto, K.. Zeta functions and topological entropy of the Markov–Dyck shifts. Münster J. Math. 4 (2011), 171–183.Google Scholar
Lind, D. A.. Entropies and factorizations of topological Markov shifts. Bull. Amer. Math. Soc. (N.S.) 9(2) (1983), 219–222.Google Scholar
Lind, D. A.. The entropies of topological Markov shifts and a related class of algebraic integers. Ergod. Th. & Dynam. Sys. 4(2) (1984), 283–300.Google Scholar
Meyerovitch, T.. Tail invariant measures of the Dyck shift. Israel J. Math. 163 (2008), 61–83.Google Scholar
Schmidt, K.. Automorphisms of compact abelian groups and affine varieties. Proc. Lond. Math. Soc. (3) 61(3) (1990), 480–496.Google Scholar
Schmidt, K.. The cohomology of higher-dimensional shifts of finite type. Pacific J. Math. 170(1) (1995), 237–269.Google Scholar
Schmidt, K.. Tilings, fundamental cocycles and fundamental groups of symbolic Z d -actions. Ergod. Th. & Dynam. Sys. 18(6) (1998), 1473–1525.Google Scholar
Weiss, B.. Actions of amenable groups. Topics in Dynamics and Ergodic Theory (London Mathematical Society Lecture Note Series, 310) . Cambridge University Press, Cambridge, 2003, pp. 226–262.Google Scholar