Research Article
Structure de certains produits semi directs
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 559-566
-
- Article
-
- You have access
- Export citation
Real analytic actions of SL (2, ℝ) on a surface
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 447-499
-
- Article
-
- You have access
- Export citation
On a construction of unitary cocycles and the representation theory of amenable groups
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 129-133
-
- Article
-
- You have access
- Export citation
Hausdorff dimension for horseshoes
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 251-260
-
- Article
-
- You have access
- Export citation
The C1 Closing Lemma, including Hamiltonians
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 261-313
-
- Article
-
- You have access
- Export citation
Persistence in expansive systems
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 567-578
-
- Article
-
- You have access
- Export citation
Geometry of the Katok examples
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 135-157
-
- Article
-
- You have access
- Export citation
Front matter
ETS volume 3 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
Periodic points of surface homeomorphisms with zero entropy
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 315-334
-
- Article
-
- You have access
- Export citation
Topological minimal self-joinings
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 579-599
-
- Article
-
- You have access
- Export citation
Errata
Errata to ‘A proof of Pesin's formula’
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 159-160
-
- Article
-
- You have access
- Export citation
Back matter
ETS volume 3 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Front matter
ETS volume 3 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
Flows associated with product type odometers
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 601-611
-
- Article
-
- You have access
- Export citation
Book Reviews
Topics in Ergodic Theory (Cambridge Tracts in Mathematics, no. 75) By William Parry: pp. 110. Cambridge University Press: Cambridge, 1981.
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 161-162
-
- Article
-
- You have access
- Export citation
Recurrence in Ergodic Theory and Combinatorial Number Theory By H. Furstenberg: pp. 199. Princeton University Press: Princeton, New Yersey, 1981
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 162-166
-
- Article
-
- You have access
- Export citation
Research Article
Embedding some transformation group C*-algebras into AF-algebras
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 613-626
-
- Article
-
- You have access
- Export citation
Back matter
ETS volume 3 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Front matter
ETS volume 3 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
Immediate conditional hyperbolicity in dynamical systems
-
- Published online by Cambridge University Press:
- 19 September 2008, pp. 627-647
-
- Article
-
- You have access
- Export citation



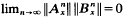 uniformly on
uniformly on 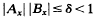 uniformly on
uniformly on