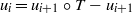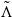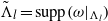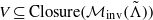Research Article
Bernoulli actions are weakly contained in any free action
-
- Published online by Cambridge University Press:
- 07 February 2012, pp. 323-333
-
- Article
- Export citation
Ultraproducts of measure preserving actions and graph combinatorics
-
- Published online by Cambridge University Press:
- 16 February 2012, pp. 334-374
-
- Article
- Export citation
On infinitely cohomologous to zero observables
-
- Published online by Cambridge University Press:
- 08 February 2012, pp. 375-399
-
- Article
- Export citation
The Poisson boundary of a locally discrete group of diffeomorphisms of the circle
-
- Published online by Cambridge University Press:
- 12 March 2012, pp. 400-415
-
- Article
- Export citation
Enumerating combinatorial classes of the complex polynomial vector fields in ℂ
-
- Published online by Cambridge University Press:
- 20 February 2012, pp. 416-440
-
- Article
- Export citation
Canonical compactifications for Markov shifts
-
- Published online by Cambridge University Press:
- 08 February 2012, pp. 441-454
-
- Article
- Export citation
On Finsler surfaces without conjugate points
-
- Published online by Cambridge University Press:
- 07 February 2012, pp. 455-474
-
- Article
- Export citation
A note on Borel–Cantelli lemmas for non-uniformly hyperbolic dynamical systems
-
- Published online by Cambridge University Press:
- 16 February 2012, pp. 475-498
-
- Article
- Export citation
Examples of amalgamated free products and coupling rigidity
-
- Published online by Cambridge University Press:
- 02 February 2012, pp. 499-528
-
- Article
- Export citation
Optimal transport and dynamics of expanding circle maps acting on measures
-
- Published online by Cambridge University Press:
- 07 February 2012, pp. 529-548
-
- Article
- Export citation
The zero-type property and mixing of Bernoulli shifts
-
- Published online by Cambridge University Press:
- 07 February 2012, pp. 549-559
-
- Article
- Export citation
Ergodic properties of invariant measures for C1+α non-uniformly hyperbolic systems
-
- Published online by Cambridge University Press:
- 08 February 2012, pp. 560-584
-
- Article
- Export citation
Diophantine approximation by orbits of expanding Markov maps
-
- Published online by Cambridge University Press:
- 07 February 2012, pp. 585-608
-
- Article
- Export citation
An L1 ergodic theorem with values in a non-positively curved space via a canonical barycenter map
-
- Published online by Cambridge University Press:
- 07 February 2012, pp. 609-623
-
- Article
- Export citation
Invariant measures with bounded variation densities for piecewise area preserving maps
-
- Published online by Cambridge University Press:
- 14 February 2012, pp. 624-642
-
- Article
- Export citation
Correction
Nonabelian free group actions: Markov processes, the Abramov–Rohlin formula and Yuzvinskii’s formula – CORRIGENDUM
-
- Published online by Cambridge University Press:
- 06 September 2012, pp. 643-645
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETDS volume 33 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 06 March 2013, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
ETDS volume 33 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 06 March 2013, pp. b1-b3
-
- Article
-
- You have access
- Export citation