Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T00:40:29.951Z Has data issue: false hasContentIssue false
  • English
  • Français

On infinitely cohomologous to zero observables

Published online by Cambridge University Press:  08 February 2012

AMANDA DE LIMA  and
DANIEL SMANIA
AMANDA DE LIMA
Affiliation:
Departamento de Matemática, ICMC-USP, Caixa Postal 668, São Carlos-SP, CEP 13560-970 São Carlos-SP, Brazil (email: [email protected], [email protected])
DANIEL SMANIA
Affiliation:
Departamento de Matemática, ICMC-USP, Caixa Postal 668, São Carlos-SP, CEP 13560-970 São Carlos-SP, Brazil (email: [email protected], [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that for a large class of piecewise expanding maps T, the bounded p-variation observables u0 that admit an infinite sequence of bounded p-variation observables ui satisfying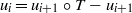

\[ u_{i}= u_{i+1}\circ T-u_{i+1} \]
are constant. The method of the proof consists of finding a suitable Hilbert basis for L2(hm), where hm is the unique absolutely continuous invariant probability of T. On this basis, the action of the Perron–Frobenius and the Koopman operator on L2(hm) can be easily understood. This result generalizes earlier results by Bamón, Kiwi, Rivera-Letelier and Urzúa for the case T(x)=ℓx mod   1 , ℓ∈ℕ∖ {0,1} and Lipschitzian observables u0.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 33 , Issue 2 , April 2013 , pp. 375 - 399
Copyright
©2012 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]de Lima, A.. Cohomologia e propriedades estocásticas de transformações expansoras e observáveis lipschitzianos. Master’s Thesis, ICMC-USP, 2007.Google Scholar
[2]Avila, A.. Personal communication, 2011.Google Scholar
[3]Baladi, V.. Positive Transfer Operators and Decay of Correlations (Advanced Series in Nonlinear Dynamics, 16). World Scientific, Singapore, 2000.Google Scholar
[4]Bamón, R., Rivera-Letelier, J., Kiwi, J. and Urzúa, R.. On the topology of solenoidal attractors of the cylinder. Ann. Inst. H. Poincaré Anal. Non Linéaire 23(2) (2006), 209–236.Google Scholar
[5]Broise, A.. Transformations Dilatantes de L’Intervalle et Théorème Limites. Études Spectrales D’Opérateurs de Transfert et Applications (Asterisque, 238). 1996.Google Scholar
[6]Goffman, C., Nishiura, T. and Waterman, D.. Homeomorphisms in Analysis (Mathematical Surveys and Monographs, 54). American Mathematical Society, 1997.Google Scholar
[7]Pollicott, M.. Meromorphic extensions of generalised zeta functions. Invent. Math. 85(1) (1986), 147–164.Google Scholar
[8]Shub, M. and Sullivan, D.. Expanding endomorphisms of the circle revisited. Ergod. Th. & Dynam. Sys. 5 (1985), 285–289.Google Scholar
[9]Viana, M.. Stochastic dynamics of deterministic systems. Colóquio Brasileiro de Matemática-IMPA (1997).Google Scholar
[10]Wong, S.. Holder continuous derivatives and ergodic theory. J. Lond. Math. Soc. s2-22(3) (1980), 506–520.Google Scholar