Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T04:19:08.889Z Has data issue: false hasContentIssue false
  • English
  • Français

Ergodic properties of invariant measures for C1+α non-uniformly hyperbolic systems

Published online by Cambridge University Press:  08 February 2012

CHAO LIANG ,
WENXIANG SUN  and
XUETING TIAN
CHAO LIANG
Affiliation:
Applied Mathematical Department, The Central University of Finance and Economics, Beijing 100081, China (email: [email protected])
WENXIANG SUN
Affiliation:
LMAM, School of Mathematical Sciences, Peking University, Beijing 100871, China (email: [email protected])
XUETING TIAN
Affiliation:
Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing 100190, China School of Mathematical Sciences, Peking University, Beijing 100871, China (email: [email protected], [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

For every ergodic hyperbolic measure ω of a C1+α diffeomorphism, there is an ω-full-measure set 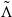$\tilde {\Lambda }$ (the union of 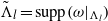$\tilde \Lambda _l=\mathrm {supp}( \omega |_{\Lambda _{l}})$, the support sets of ω on each Pesin block Λl, l=1,2,…) such that every non-empty, compact and connected subset 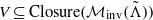$V\subseteq \mathrm {Closure}(\mathcal {M}_{\mathrm {inv}}(\tilde \Lambda ))$ coincides with Vf(x), where 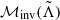$\mathcal {M}_{\mathrm {inv}}(\tilde {\Lambda })$ denotes the space of invariant measures supported on 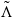$\tilde {\Lambda }$ and Vf(x) denotes the accumulation set of time averages of Dirac measures supported at one orbit of some point x. For each fixed set V, the points with the above property are dense in the support supp (ω) . In particular, points satisfying $V_f(x)=\mathrm {Closure}(\mathcal {M}_{\mathrm {inv}}(\tilde \Lambda ))$ are dense in supp (ω) . Moreover, if supp (ω) is isolated, the points satisfying $V_f(x)\supseteq \mathrm {Closure}(\mathcal {M}_{\mathrm {inv}}(\tilde \Lambda ))$ form a residual subset of supp (ω) . These extend results of K. Sigmund [On dynamical systems with the specification property. Trans. Amer. Math. Soc. 190 (1974), 285–299] (see also M. Denker, C. Grillenberger and K. Sigmund [Ergodic Theory on Compact Spaces (Lecture Notes in Mathematics, 527). Springer, Berlin, Ch. 21]) from the uniformly hyperbolic case to the non-uniformly hyperbolic case. As a corollary, irregular + points form a residual set of supp (ω) .

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 33 , Issue 2 , April 2013 , pp. 560 - 584
Copyright
©2012 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Abdenur, F., Bonatti, C. and Crovisier, S.. Non-uniform hyperbolicity of C 1-generic diffeomorphisms. Israel J. Math. to appear.Google Scholar
[2]Bochi, J.. Genericity of zero Lyapunov exponents. Ergod. Th. & Dynam. Sys. 22 (2002), 1667–1696.Google Scholar
[3]Bowen, R.. Periodic orbits for hyperbolic flows. Amer. J. Math. 94 (1972), 1–30.Google Scholar
[4]Denker, M., Grillenberger, C. and Sigmund, K.. Ergodic Theory on Compact Spaces (Lecture Notes in Mathematics, 527). Springer, Berlin.Google Scholar
[5]Hirayama, M.. Periodic probability measures are dense in the set of invariant measures. Discrete Contin. Dyn. Syst. 9 (2003), 1185–1192.Google Scholar
[6]Katok, A.. Liapunov exponents, entropy and periodic orbits for diffeomorphisms. Publ. Math. Inst. Hautes Études Sci. 51 (1980), 137–173.Google Scholar
[7]Liang, C., Liu, G. and Sun, W.. Approximation properties on invariant measure and Oseledec splitting in non-uniformly hyperbolic systems. Trans. Amer. Math. Soc. 361 (2009), 1543–1579.Google Scholar
[8]Oseledec, V. I.. Multiplicative ergodic theorem, Liapunov characteristic numbers for dynamical systems. Trans. Moscow Math. Soc. 19 (1968), 197–221, translated from Russian.Google Scholar
[9]Pfister, C. and Sullivan, W.. On the topological entropy of saturated sets. Ergod. Th. & Dynam. Sys. 27 (2007), 929–956.Google Scholar
[10]Pollicott, M.. Lectures on Ergodic Theory and Pesin Theory on Compact Manifolds. Cambridge University Press, Cambridge, 1993.Google Scholar
[11]Sigmund, K.. Generic properties of invariant measures for Axiom A-diffeomorphisms. Invent. Math. 11 (1970), 99–109.Google Scholar
[12]Sigmund, K.. On dynamical systems with the specification property. Trans. Amer. Math. Soc. 190 (1974), 285–299.Google Scholar
[13]Sun, W. and Tian, X.. Pesin set, closing lemma and shadowing lemma in C 1 non-uniformly hyperbolic systems with limit domination, arXiv:1004.0486.Google Scholar
[14]Sun, W. and Tian, X.. The structure on invariant measures of C 1 generic diffeomorphisms. Acta Math. Sinica to appear.Google Scholar
[15]Walters, P.. An Introduction to Ergodic Theory. Springer, Berlin, 2001.Google Scholar