Ledingham and Penfold have shown that during the lag-phase of growth of B. coli in a nutrient medium the time and bacilli are connected by an equation of the form Xn=K log Y where n and k are constants (the initial seeding = 1). It has been pointed out in this communication that there is a relationship between n and k, and that the above equation can be put in the form
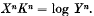
The advantage of this new equation is that K remains of the same value throughout the whole series of experiments.
In the case investigated by Ledingham and Penfold the constant of unrestricted growth is approximately equal to 2K.
The equation can also be put in the form
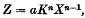
where Z is the “constant” of growth 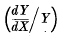 at a time X. By suitably adjusting n and a this equation can be made to represent not only the lag-phase of growth but also the logarithmic phase, and the special phase of retarded growth when the X − Y curve is rectilinear. When cell-death occurs the bacteria usually perish at such a rate that the X − Y curve is logarithmic; the general equation therefore also covers this case.
at a time X. By suitably adjusting n and a this equation can be made to represent not only the lag-phase of growth but also the logarithmic phase, and the special phase of retarded growth when the X − Y curve is rectilinear. When cell-death occurs the bacteria usually perish at such a rate that the X − Y curve is logarithmic; the general equation therefore also covers this case.

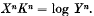
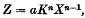
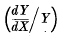 at a time
at a time