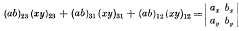Research Article
A note on the ruled surface
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. i-ii
-
- Article
-
- You have access
- Export citation
A series identity
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. iii-iv
-
- Article
-
- You have access
- Export citation
On the configuration known as a double-six of lines
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. iv-vi
-
- Article
-
- You have access
- Export citation
The evaluation of certain continued fractions
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. vi-x
-
- Article
-
- You have access
- Export citation
On the centre of spherical curvature of a curve
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. xi-xii
-
- Article
-
- You have access
- Export citation
The advantage of differentials in the technique of differentiation
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. xii-xiv
-
- Article
-
- You have access
- Export citation
Note on a special determinant
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. xxvii-xviii
-
- Article
-
- You have access
- Export citation
Bi-determinants
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. xv-xxi
-
- Article
-
- You have access
- Export citation
Pictorial relativity
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. xxi-xxvi
-
- Article
-
- You have access
- Export citation


 , and this equation will generate another continued fraction. After a little rearrangement of the first two members it appears that (1) implies
, and this equation will generate another continued fraction. After a little rearrangement of the first two members it appears that (1) implies