Hostname: page-component-f554764f5-8cg97 Total loading time: 0 Render date: 2025-04-22T05:00:54.218Z Has data issue: false hasContentIssue false
  • English
  • Français

Bi-determinants

Published online by Cambridge University Press:  31 October 2008

H. W. Turnbull
H. W. Turnbull
Affiliation:
University of St Andrews.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The important Binet-Cauchy theorem of determinants (3, p. 81)

may be illustrated as follows. Consider the identity

where ax = a1x1 + a2x2 + a3x3, and similarly for ay, bx, by. This identity follows by adding x1 row1 + x2row2 + x3row3 to row4 in the first determinant; and y1row1 + etc. to row5. Then by expanding both determinants in a Laplace development of the first three rows and the last two we obtain the identity

.

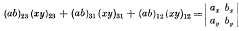Type
Research Article
Information
Edinburgh Mathematical Notes , Volume 30 , January 1937 , pp. xv - xxi
Copyright
Copyright © Edinburgh Mathematical Society 1937

References

REFERENCES

1. Muir : History of Determinants.Google Scholar
2.Muir, and Metzler, (New York, 1930), Theory of Determinants.Google Scholar
3.Turnbull, : Theory of determinants, matrices and invariants (1928).Google Scholar
4.Turnbull, and Aitken, : Canonical Matrices (1932).Google Scholar