With analytic applications in mind, in particular beyond endoscopy, we initiate the study of the elliptic part of the trace formula. Incorporating the approximate functional equation into the elliptic part, we control the analytic behavior of the volumes of tori that appear in the elliptic part. Furthermore, by carefully choosing the truncation parameter in the approximate functional equation, we smooth out the singularities of orbital integrals. Finally, by an application of Poisson summation we rewrite the elliptic part so that it is ready to be used in analytic applications, and in particular in beyond endoscopy. As a by product we also isolate the contributions of special representations as pointed out in [Beyond endoscopy, in Contributions to automorphic forms, geometry and number theory (Johns Hopkins University Press, Baltimore, MD, 2004), 611–697].

We study the growth of \unicode[STIX]{x0428}$\unicode[STIX]{x0428}$ and p^{\infty }$p^{\infty }$-Selmer groups for isogenous abelian varieties in towers of number fields, with an emphasis on elliptic curves. The growth types are usually exponential, as in the ‘positive {\it\mu}${\it\mu}$-invariant’ setting in the Iwasawa theory of elliptic curves. The towers we consider are p$p$-adic and l$l$-adic Lie extensions for l\neq p$l\neq p$, in particular cyclotomic and other \mathbb{Z}_{l}$\mathbb{Z}_{l}$-extensions.

We compute the p$p$-adic L$L$-functions of evil Eisenstein series, showing that they factor as products of two Kubota–Leopoldt p$p$-adic L$L$-functions times a logarithmic term. This proves in particular a conjecture of Glenn Stevens.

We prove that formal Fourier Jacobi expansions of degree two are Siegel modular forms. As a corollary, we deduce modularity of the generating function of special cycles of codimension two, which were defined by Kudla. A second application is the proof of termination of an algorithm to compute Fourier expansions of arbitrary Siegel modular forms of degree two. Combining both results enables us to determine relations of special cycles in the second Chow group.

Let K$K$ be a totally real field. By the asymptotic Fermat’s Last Theorem overK$K$ we mean the statement that there is a constant B_{K}$B_{K}$ such that for any prime exponent p>B_{K}$p>B_{K}$, the only solutions to the Fermat equation

\begin{eqnarray}a^{p}+b^{p}+c^{p}=0,\quad a,b,c\in K\end{eqnarray} $$\begin{eqnarray}a^{p}+b^{p}+c^{p}=0,\quad a,b,c\in K\end{eqnarray}$$

abc=0$abc=0$

K$K$

K$K$

K=\mathbb{Q}(\sqrt{d})$K=\mathbb{Q}(\sqrt{d})$

d\geqslant 2$d\geqslant 2$

{\textstyle \frac{5}{6}}${\textstyle \frac{5}{6}}$

1$1$

Let p\geqslant 5$p\geqslant 5$ be a prime. If an irreducible component of the spectrum of the ‘big’ ordinary Hecke algebra does not have complex multiplication, under mild assumptions, we prove that the image of its Galois representation contains, up to finite error, a principal congruence subgroup {\rm\Gamma}(L)${\rm\Gamma}(L)$ of \text{SL}_{2}(\mathbb{Z}_{p}[[T]])$\text{SL}_{2}(\mathbb{Z}_{p}[[T]])$ for a principal ideal (L)\neq 0$(L)\neq 0$ of \mathbb{Z}_{p}[[T]]$\mathbb{Z}_{p}[[T]]$ for the canonical ‘weight’ variable t=1+T$t=1+T$. If L\notin {\rm\Lambda}^{\times }$L\notin {\rm\Lambda}^{\times }$, the power series L$L$ is proven to be a factor of the Kubota–Leopoldt p$p$-adic L$L$-function or of the square of the anticyclotomic Katz p$p$-adic L$L$-function or a power of (t^{p^{m}}-1)$(t^{p^{m}}-1)$.

The celebrated Smith–Minkowski–Siegel mass formula expresses the mass of a quadratic lattice (L,Q)$(L,Q)$ as a product of local factors, called the local densities of (L,Q)$(L,Q)$. This mass formula is an essential tool for the classification of integral quadratic lattices. In this paper, we will describe the local density formula explicitly by observing the existence of a smooth affine group scheme \underline{G}$\underline{G}$ over \mathbb{Z}_{2}$\mathbb{Z}_{2}$ with generic fiber \text{Aut}_{\mathbb{Q}_{2}}(L,Q)$\text{Aut}_{\mathbb{Q}_{2}}(L,Q)$, which satisfies \underline{G}(\mathbb{Z}_{2})=\text{Aut}_{\mathbb{Z}_{2}}(L,Q)$\underline{G}(\mathbb{Z}_{2})=\text{Aut}_{\mathbb{Z}_{2}}(L,Q)$. Our method works for any unramified finite extension of \mathbb{Q}_{2}$\mathbb{Q}_{2}$. Therefore, we give a long awaited proof for the local density formula of Conway and Sloane and discover its generalization to unramified finite extensions of \mathbb{Q}_{2}$\mathbb{Q}_{2}$. As an example, we give the mass formula for the integral quadratic form Q_{n}(x_{1},\dots ,x_{n})=x_{1}^{2}+\cdots +x_{n}^{2}$Q_{n}(x_{1},\dots ,x_{n})=x_{1}^{2}+\cdots +x_{n}^{2}$ associated to a number field k$k$ which is totally real and such that the ideal (2)$(2)$ is unramified over k$k$.

We develop spectral theory for the generator of the q$q$-Boson (stochastic) particle system. Our central result is a Plancherel type isomorphism theorem for this system. This theorem has various implications. It proves the completeness of the Bethe ansatz for the q$q$-Boson generator and consequently enables us to solve the Kolmogorov forward and backward equations for general initial data. Owing to a Markov duality with q$q$-TASEP (q$q$-deformed totally asymmetric simple exclusion process), this leads to moment formulas which characterize the fixed time distribution of q$q$-TASEP started from general initial conditions. The theorem also implies the biorthogonality of the left and right eigenfunctions. We consider limits of our q$q$-Boson results to a discrete delta Bose gas considered previously by van Diejen, as well as to another discrete delta Bose gas that describes the evolution of moments of the semi-discrete stochastic heat equation (or equivalently, the O’Connell–Yor semi-discrete directed polymer partition function). A further limit takes us to the delta Bose gas which arises in studying moments of the stochastic heat equation/Kardar–Parisi–Zhang equation.

In this paper we prove that a pure, regular, totally odd, polarizable weakly compatible system of l$l$-adic representations is potentially automorphic. The innovation is that we make no irreducibility assumption, but we make a purity assumption instead. For compatible systems coming from geometry, purity is often easier to check than irreducibility. We use Katz’s theory of rigid local systems to construct many examples of motives to which our theorem applies. We also show that if F$F$ is a CM or totally real field and if {\it\pi}${\it\pi}$ is a polarizable, regular algebraic, cuspidal automorphic representation of \text{GL}_{n}(\mathbb{A}_{F})$\text{GL}_{n}(\mathbb{A}_{F})$, then for a positive Dirichlet density set of rational primes l$l$, the l$l$-adic representations r_{l,\imath }({\it\pi})$r_{l,\imath }({\it\pi})$ associated to {\it\pi}${\it\pi}$ are irreducible.

We construct an Euler system attached to a weight 2 modular form twisted by a Grössencharacter of an imaginary quadratic field K$K$, and apply this to bounding Selmer groups.

In this paper, we study the structure of the local components of the (shallow, i.e. without U_{p}$U_{p}$) Hecke algebras acting on the space of modular forms modulo p$p$ of level 1$1$, and relate them to pseudo-deformation rings. In many cases, we prove that those local components are regular complete local algebras of dimension 2$2$, generalizing a recent result of Nicolas and Serre for the case p=2$p=2$.

For non-singular intersections of pairs of quadrics in 11 or more variables, we prove an asymptotic for the number of rational points in an expanding box.

We establish the existence of smooth transfer for Guo–Jacquet relative trace formulae in the p$p$-adic case. This kind of smooth transfer is a key step towards a generalization of Waldspurger’s result on central values of L-functions of \text{GL}_{2}$\text{GL}_{2}$.

Nonsingular projective 3-folds V$V$ of general type can be naturally classified into 18 families according to the pluricanonical section index{\it\delta}(V):=\text{min}\{m\mid P_{m}\geqslant 2\}${\it\delta}(V):=\text{min}\{m\mid P_{m}\geqslant 2\}$ since 1\leqslant {\it\delta}(V)\leqslant 18$1\leqslant {\it\delta}(V)\leqslant 18$ due to our previous series (I, II). Based on our further classification to 3-folds with {\it\delta}(V)\geqslant 13${\it\delta}(V)\geqslant 13$ and an intensive geometrical investigation to those with {\it\delta}(V)\leqslant 12${\it\delta}(V)\leqslant 12$, we prove that \text{Vol}(V)\geqslant \frac{1}{1680}$\text{Vol}(V)\geqslant \frac{1}{1680}$ and that the pluricanonical map {\rm\Phi}_{m}${\rm\Phi}_{m}$ is birational for all m\geqslant 61$m\geqslant 61$, which greatly improves known results. An optimal birationality of {\rm\Phi}_{m}${\rm\Phi}_{m}$ for the case {\it\delta}(V)=2${\it\delta}(V)=2$ is obtained. As an effective application, we study projective 4-folds of general type with p_{g}\geqslant 2$p_{g}\geqslant 2$ in the last section.

We show that arithmetic local constants attached by Mazur and Rubin to pairs of self-dual Galois representations which are congruent modulo a prime number p>2$p>2$ are compatible with the usual local constants at all primes not dividing p$p$ and in two special cases also at primes dividing p$p$. We deduce new cases of the p$p$-parity conjecture for Selmer groups of abelian varieties with real multiplication (Theorem 4.14) and elliptic curves (Theorem 5.10).

An integer n$n$ is said to be y$y$-friable if its largest prime factor P^{+}(n)$P^{+}(n)$ is less than y$y$. In this paper, it is shown that the y$y$-friable integers less than x$x$ have a weak exponent of distribution at least 3/5-{\it\varepsilon}$3/5-{\it\varepsilon}$ when (\log x)^{c}\leqslant x\leqslant x^{1/c}$(\log x)^{c}\leqslant x\leqslant x^{1/c}$ for some c=c({\it\varepsilon})\geqslant 1$c=c({\it\varepsilon})\geqslant 1$, that is to say, they are well distributed in the residue classes of a fixed integer a$a$, on average over moduli {\leqslant}x^{3/5-{\it\varepsilon}}${\leqslant}x^{3/5-{\it\varepsilon}}$ for each fixed a\neq 0$a\neq 0$ and {\it\varepsilon}>0${\it\varepsilon}>0$. We apply this to the estimation of the sum \sum _{2\leqslant n\leqslant x,P^{+}(n)\leqslant y}{\it\tau}(n-1)$\sum _{2\leqslant n\leqslant x,P^{+}(n)\leqslant y}{\it\tau}(n-1)$ when (\log x)^{c}\leqslant y$(\log x)^{c}\leqslant y$. This follows and improves on previous work of Fouvry and Tenenbaum. Our proof combines the dispersion method of Linnik in the setting of Bombieri, Fouvry, Friedlander and Iwaniec with recent work of Harper on friable integers in arithmetic progressions.

Let A$A$ be an abelian variety over a global field K$K$ of characteristic p\geqslant 0$p\geqslant 0$. If A$A$ has nontrivial (respectively full) K$K$-rational l$l$-torsion for a prime l\neq p$l\neq p$, we exploit the fppf cohomological interpretation of the l$l$-Selmer group \text{Sel}_{l}\,A$\text{Sel}_{l}\,A$ to bound \#\text{Sel}_{l}\,A$\#\text{Sel}_{l}\,A$ from below (respectively above) in terms of the cardinality of the l$l$-torsion subgroup of the ideal class group of K$K$. Applied over families of finite extensions of K$K$, the bounds relate the growth of Selmer groups and class groups. For function fields, this technique proves the unboundedness of l$l$-ranks of class groups of quadratic extensions of every K$K$ containing a fixed finite field \mathbb{F}_{p^{n}}$\mathbb{F}_{p^{n}}$ (depending on l$l$). For number fields, it suggests a new approach to the Iwasawa {\it\mu}=0${\it\mu}=0$ conjecture through inequalities, valid when A(K)[l]\neq 0$A(K)[l]\neq 0$, between Iwasawa invariants governing the growth of Selmer groups and class groups in a \mathbb{Z}_{l}$\mathbb{Z}_{l}$-extension.

In this article we explain how the results in our previous article on ‘algebraic Hecke characters and compatible systems of mod p$p$ Galois representations over global fields’ allow one to attach a Hecke character to every cuspidal Drinfeld modular eigenform from its associated crystal that was constructed in earlier work of the author. On the technical side, we prove along the way a number of results on endomorphism rings of {\it\tau}${\it\tau}$-sheaves and crystals. These are needed to exhibit the close relation between Hecke operators as endomorphisms of crystals on the one side and Frobenius automorphisms acting on étale sheaves associated to crystals on the other. We also present some partial results on the ramification of Hecke characters associated to Drinfeld modular eigenforms. An important phenomenon absent from the case of classical modular forms is that ramification can also result from places of modular curves of good but non-ordinary reduction. In an appendix, jointly with Centeleghe we prove some basic results on p$p$-adic Galois representations attached to \text{GL}_{2}$\text{GL}_{2}$-type cuspidal automorphic forms over global fields of characteristic p$p$.

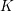Let K$K$ be a number field. 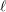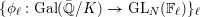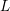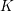For any system of semisimple mod \ell$\ell$ Galois representations \{{\it\phi}_{\ell }:\text{Gal}(\bar{\mathbb{Q}}/K)\rightarrow \text{GL}_{N}(\mathbb{F}_{\ell })\}_{\ell }$\{{\it\phi}_{\ell }:\text{Gal}(\bar{\mathbb{Q}}/K)\rightarrow \text{GL}_{N}(\mathbb{F}_{\ell })\}_{\ell }$ arising from étale cohomology (Definition 1), there exists a finite normal extension L$L$ of K$K$ such that if we denote 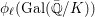{\it\phi}_{\ell }(\text{Gal}(\bar{\mathbb{Q}}/K))${\it\phi}_{\ell }(\text{Gal}(\bar{\mathbb{Q}}/K))$ and 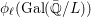{\it\phi}_{\ell }(\text{Gal}(\bar{\mathbb{Q}}/L))${\it\phi}_{\ell }(\text{Gal}(\bar{\mathbb{Q}}/L))$ by 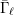\bar{{\rm\Gamma}}_{\ell }$\bar{{\rm\Gamma}}_{\ell }$ and 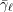\bar{{\it\gamma}}_{\ell }$\bar{{\it\gamma}}_{\ell }$, respectively, for all 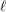\ell$\ell$ and let 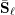\bar{\mathbf{S}}_{\ell }$\bar{\mathbf{S}}_{\ell }$ be the 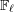\mathbb{F}_{\ell }$\mathbb{F}_{\ell }$-semisimple subgroup of 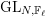\text{GL}_{N,\mathbb{F}_{\ell }}$\text{GL}_{N,\mathbb{F}_{\ell }}$ associated to 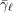\bar{{\it\gamma}}_{\ell }$\ba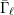r{{\it\gamma}}_{\ell }$ (or \bar{{\rm\Gamma}}_{\ell }$\bar{{\rm\Gamma}}_{\ell }$) by Nori’s theory [On subgroups of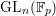\text{GL}_{n}(\mathbb{F}_{p})$\text{GL}_{n}(\mathbb{F}_{p})$, Invent. Math. 88 (1987), 257–275] for sufficiently large 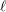\ell$\ell$, then the following statements hold for all sufficiently large 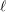\ell$\ell$.

A(i) The formal character of 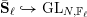\bar{\mathbf{S}}_{\ell }{\hookrightarrow}\text{GL}_{N,\mathbb{F}_{\ell }}$\bar{\mathbf{S}}_{\ell }{\hookrightarrow}\text{GL}_{N,\mathbb{F}_{\ell }}$ (Definition 1) is independent of 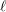\ell$\ell$ and equal to the formal character of 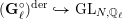(\mathbf{G}_{\ell }^{\circ })^{\text{der}}{\hookrightarrow}\text{GL}_{N,\mathbb{Q}_{\ell }}$(\mathbf{G}_{\ell }^{\circ })^{\text{der}}{\hookrightarrow}\text{GL}_{N,\mathbb{Q}_{\ell }}$, where 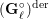(\mathbf{G}_{\ell }^{\circ })^{\text{der}}$(\mathbf{G}_{\ell }^{\circ })^{\text{der}}$ is the derived group of the identity component of 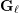\mathbf{G}_{\ell }$\mathbf{G}_{\ell }$, the monodromy group of the corresponding semi-simplified 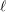\ell$\ell$-adic Galois representation 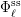{\rm\Phi}_{\ell }^{\text{ss}}${\rm\Phi}_{\ell }^{\text{ss}}$.

A(ii) The non-cyclic composition factors of 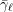\bar{{\it\gamma}}_{\ell }$\bar{{\it\gamma}}_{\ell }$ and 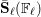\bar{\mathbf{S}}_{\ell }(\mathbb{F}_{\ell })$\bar{\mathbf{S}}_{\ell }(\mathbb{F}_{\ell })$ are identical. Therefore, the composition factors of 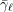\bar{{\it\gamma}}_{\ell }$\bar{{\it\gamma}}_{\ell }$ are finite simple groups of Lie type of characteristic 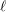\ell$\ell$ and are cyclic groups.

B(i) The total 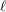\ell$\ell$-r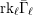ank \text{rk}_{\ell }\bar{{\rm\Gamma}}_{\ell }$\text{rk}_{\ell }\bar{{\rm\Gamma}}_{\ell }$ of 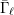\bar{{\rm\Gamma}}_{\ell }$\bar{{\rm\Gamma}}_{\ell }$ (Definition 14) is equal to the rank of 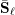\bar{\mathbf{S}}_{\ell }$\bar{\mathbf{S}}_{\ell }$ and is therefore independent of 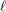\ell$\ell$.

B(ii) The 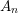A_{n}$A_{n}$-type 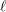\ell$\ell$-r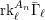ank \text{rk}_{\ell }^{A_{n}}\bar{{\rm\Gamma}}_{\ell }$\text{rk}_{\ell }^{A_{n}}\bar{{\rm\Gamma}}_{\ell }$ of 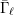\bar{{\rm\Gamma}}_{\ell }$\bar{{\rm\Gamma}}_{\ell }$ (Definition 14) for 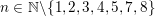n\in \mathbb{N}\setminus \{1,2,3,4,5,7,8\}$n\in \mathbb{N}\setminus \{1,2,3,4,5,7,8\}$ and the parity of 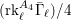(\text{rk}_{\ell }^{A_{4}}\bar{{\rm\Gamma}}_{\ell })/4$(\text{rk}_{\ell }^{A_{4}}\bar{{\rm\Gamma}}_{\ell })/4$ are independent of 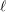\ell$\ell$.

The Kodaira–Thurston manifold is a quotient of a nilpotent Lie group by a cocompact lattice. We compute the family Gromov–Witten invariants which count pseudoholomorphic tori in the Kodaira–Thurston manifold. For a fixed symplectic form the Gromov–Witten invariant is trivial so we consider the twistor family of left-invariant symplectic forms which are orthogonal for some fixed metric on the Lie algebra. This family defines a loop in the space of symplectic forms. This is the first example of a genus one family Gromov–Witten computation for a non-Kähler manifold.