Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-04T21:24:14.788Z Has data issue: false hasContentIssue false
  • English
  • Français

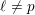Compatibility of arithmetic and algebraic local constants (the case $\ell \neq p$)

Part of: Algebraic number theory: local and $p$-adic fields Arithmetic algebraic geometry

Published online by Cambridge University Press:  08 April 2015

Jan Nekovář
Jan Nekovář*
Affiliation:
Université Pierre et Marie Curie (Paris 6), Institut de Mathématiques de Jussieu, Théorie des Nombres, Case 247, 4 place Jussieu, F-75252, Paris cedex 05, France email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

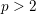We show that arithmetic local constants attached by Mazur and Rubin to pairs of self-dual Galois representations which are congruent modulo a prime number $p>2$ are compatible with the usual local constants at all primes not dividing 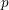$p$ and in two special cases also at primes dividing 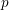$p$. We deduce new cases of the 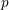$p$-parity conjecture for Selmer groups of abelian varieties with real multiplication (Theorem 4.14) and elliptic curves (Theorem 5.10).

Keywords

local constantsSelmer groupsparity conjectureelliptic curves

MSC classification

Primary: 11G05: Elliptic curves over global fields 11G40: $L$-functions of varieties over global fields; Birch-Swinnerton-Dyer conjecture 11S40: Zeta functions and $L$-functions
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 9 , September 2015 , pp. 1626 - 1646
Copyright
© The Author 2015 

References

Barnet-Lamb, T., Gee, T., Geraghty, D. and Taylor, R., Potential automorphy and change of weight, Ann. of Math. (2) 179 (2014), 501–609.CrossRefGoogle Scholar
Bloch, S. and Kato, K., L-functions and Tamagawa numbers of motives, in The Grothendieck Festschrift I, Progress in Mathematics, vol. 86 (Birkhäuser, Boston, 1990), 333–400.Google Scholar
Česnavičius, K., The $p$-parity conjecture for elliptic curves with a $p$-isogeny, J. Reine Angew. Math., doi:10.1515/crelle-2014-0040.CrossRefGoogle Scholar
Chetty, S., Comparing local constants of elliptic curves in dihedral extensions, Preprint (2010), arXiv:1002.2671.Google Scholar
Coates, J., Fukaya, T., Kato, K. and Sujatha, R., Root numbers, Selmer groups and non-commutative Iwasawa theory, J. Algebraic Geom. 19 (2010), 19–97.CrossRefGoogle Scholar
Deligne, P., Les constantes des équations fonctionnelles des fonctions L, in Modular functions of one variable II (Antwerp, 1972), Lecture Notes in Mathematics, vol. 349 (Springer, Berlin, 1973), 501–597.CrossRefGoogle Scholar
Deligne, P. and Serre, J.-P., Formes modulaires de poids 1, Ann. Sci. Éc. Norm. Supér. (4) 7 (1974), 507–530.CrossRefGoogle Scholar
Dokchitser, T. and Dokchitser, V., Regulator constants and the parity conjecture, Invent. Math. 178 (2009), 23–71.CrossRefGoogle Scholar
Dokchitser, T. and Dokchitser, V., Root numbers and parity of ranks of elliptic curves, J. Reine Angew. Math. 658 (2011), 39–64.Google Scholar
Flach, M., A generalization of the Cassels–Tate pairing, J. reine angew. Math. 412 (1990), 113–127.Google Scholar
Fontaine, J.-M., Représentations ℓ-adiques potentiellement semi-stables, in Périodes p-adiques (Bures-sur-Yvette, 1988), Astérisque, vol. 223 (Société Mathématique de France, Paris, 1994), 321–347.Google Scholar
Fontaine, J.-M. and Mazur, B., Geometric Galois representations, in Elliptic curves, modular forms and Fermat’s last theorem (Hong Kong, 1993), Series on Number Theory, vol. I (International Press, Cambridge, MA, 1995), 41–78.Google Scholar
Fontaine, J.-M. and Perrin-Riou, B., Autour des conjectures de Bloch et Kato: cohomologie galoisienne et valeurs de fonctions L, in Motives (Seattle, 1991), Proceedings of Symposia in Pure Mathematics, vol. 55/I (American Mathematical Society, Providence, RI, 1994), 599–706.CrossRefGoogle Scholar
Fröhlich, A. and Taylor, M. J., Algebraic number theory, Cambridge Studies in Advanced Mathematics, vol. 27 (Cambridge University Press, Cambridge, 1993).Google Scholar
Gross, B. H., Arithmetic on elliptic curves with complex multiplication, Lecture Notes in Mathematics, vol. 776 (Springer, Berlin, 1980).CrossRefGoogle Scholar
Klagsbrun, Z., Mazur, B. and Rubin, K., Disparity in Selmer ranks of quadratic twists of elliptic curves, Ann. of Math. (2) 178 (2013), 287–320.CrossRefGoogle Scholar
Mazur, B., Rational points of abelian varieties with values in towers of number fields, Invent. Math. 18 (1972), 183–266.CrossRefGoogle Scholar
Mazur, B. and Rubin, K., Kolyvagin systems, in Memoirs of the American Mathematical Society, no. 799, vol. 168 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Mazur, B. and Rubin, K., Finding large Selmer rank via an arithmetic theory of local constants, Ann. of Math. (2) 166 (2007), 581–614.CrossRefGoogle Scholar
Mazur, B. and Rubin, K., Growth of Selmer rank in nonabelian extensions of number fields, Duke Math. J. 143 (2008), 437–461.CrossRefGoogle Scholar
Nakamura, T., A classification of Q -curves with complex multiplication, J. Math. Soc. Japan 56 (2004), 635–648.CrossRefGoogle Scholar
Nekovář, J., Selmer complexes, Astérisque, vol. 310 (Société Mathématique de France, Paris, 2006).Google Scholar
Nekovář, J., On the parity of ranks of Selmer groups III, Doc. Math. 12 (2007), 243–274; Erratum: Doc. Math. 14 (2009), 191–194.CrossRefGoogle Scholar
Nekovář, J., On the parity of ranks of Selmer groups IV, Compositio Math. 145 (2009), 1351–1359.CrossRefGoogle Scholar
Nekovář, J., Level raising and anticyclotomic Selmer groups for Hilbert modular forms of weight two, Canad. J. Math. 64 (2012), 588–668.CrossRefGoogle Scholar
Nekovář, J., Some consequences of a formula of Mazur and Rubin for arithmetic local constants, Algebra Number Theory 7 (2013), 1101–1120.CrossRefGoogle Scholar
Raynaud, M., Schémas en groupes de type (p, …, p), Bull. Soc. Math. France 102 (1974), 241–280.CrossRefGoogle Scholar
Ribet, K., Raising the levels of modular representations, in Séminaire de Théorie des Nombres, Paris 1987–88, Progress in Mathematics, vol. 81 (Birkhäuser, Boston, 1990), 259–271.Google Scholar
Rohrlich, D., Elliptic curves with good reduction everywhere, J. Lond. Math. Soc. (2) 25 (1982), 216–222.CrossRefGoogle Scholar
Shimura, G., On the zeta-function of an abelian variety with complex multiplication, Ann. of Math. (2) 94 (1971), 504–533.CrossRefGoogle Scholar
Taylor, R., On Galois representations associated to Hilbert modular forms, Invent. Math. 98 (1989), 265–280.CrossRefGoogle Scholar
Weinberger, P.J., Exponents of the class groups of complex quadratic fields, Acta Arith. 22 (1973), 117–124.CrossRefGoogle Scholar
Wintenberger, J.-P., Potential modularity of elliptic curves over totally real fields, appendix to [Nek09].Google Scholar