Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
BENNETT, MICHAEL A.
DAHMEN, SANDER R.
MIGNOTTE, MAURICE
and
SIKSEK, SAMIR
2015.
Shifted powers in binary recurrence sequences.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 158,
Issue. 2,
p.
305.
Anni, Samuele
and
Siksek, Samir
2015.
On Serre’s uniformity conjecture for semistable elliptic curves over totally real fields.
Mathematische Zeitschrift,
Vol. 281,
Issue. 1-2,
p.
193.
Freitas, Nuno
and
Siksek, Samir
2015.
Fermat’s last theorem over some small real quadratic fields.
Algebra & Number Theory,
Vol. 9,
Issue. 4,
p.
875.
Bennett, Michael
Mihăilescu, Preda
and
Siksek, Samir
2016.
Open Problems in Mathematics.
p.
173.
Anni, Samuele
and
Siksek, Samir
2016.
Modular elliptic curves over real abelian fields and the generalized Fermat equation x2ℓ+ y2m= zp.
Algebra & Number Theory,
Vol. 10,
Issue. 6,
p.
1147.
Ţurcaş, George C.
2018.
On Fermat’s equation over some quadratic imaginary number fields.
Research in Number Theory,
Vol. 4,
Issue. 2,
Kraus, Alain
2019.
Le théorème de Fermat sur certains corps de
nombres totalement réels.
Algebra & Number Theory,
Vol. 13,
Issue. 2,
p.
301.
Bennett, Michael A.
Patel, Vandita
and
Siksek, Samir
2019.
Shifted powers in Lucas–Lehmer sequences.
Research in Number Theory,
Vol. 5,
Issue. 1,
Kara, Yasemin
and
Ozman, Ekin
2020.
Asymptotic generalized Fermat’s last theorem over number fields.
International Journal of Number Theory,
Vol. 16,
Issue. 05,
p.
907.
Freitas, Nuno
Kraus, Alain
and
Siksek, Samir
2020.
On asymptotic Fermat over ℤp-extensions of
ℚ.
Algebra & Number Theory,
Vol. 14,
Issue. 9,
p.
2571.
Freitas, Nuno
Kraus, Alain
and
Siksek, Samir
2020.
Class field theory, Diophantine analysis and the asymptotic Fermat's Last Theorem.
Advances in Mathematics,
Vol. 363,
Issue. ,
p.
106964.
Ţurcaş, George C.
2020.
On Serre's modularity conjecture and Fermat's equation over quadratic imaginary fields of class number one.
Journal of Number Theory,
Vol. 209,
Issue. ,
p.
516.
Alvarado, Alejandra
Koutsianas, Angelos
Malmskog, Beth
Rasmussen, Christopher
Vincent, Christelle
and
West, Mckenzie
2021.
Arithmetic Geometry, Number Theory, and Computation.
p.
1.
Triantafillou, Nicholas
2021.
There are no exceptional units in number fields of degree prime to 3 where 3 splits completely.
Proceedings of the American Mathematical Society, Series B,
Vol. 8,
Issue. 31,
p.
371.
Badr, Eslam
and
Bars, Francesc
2021.
Bielliptic smooth plane curves and quadratic points.
International Journal of Number Theory,
Vol. 17,
Issue. 04,
p.
1047.
Najman, Filip
and
Ţurcaş, George C.
2021.
Irreducibility of mod p Galois representations of elliptic curves with multiplicative reduction over number fields.
International Journal of Number Theory,
Vol. 17,
Issue. 08,
p.
1729.
Freitas, Nuno
Kraus, Alain
and
Siksek, Samir
2021.
Local criteria for the unit equation and the asymptotic Fermat’s Last Theorem.
Proceedings of the National Academy of Sciences,
Vol. 118,
Issue. 12,
van Langen, Joey M.
2021.
On the sum of fourth powers in arithmetic progression.
International Journal of Number Theory,
Vol. 17,
Issue. 01,
p.
191.
Michaud‐Jacobs, Philippe
2022.
On some generalized Fermat equations of the form x2+y2n=zp$x^2+y^{2n} = z^p$.
Mathematika,
Vol. 68,
Issue. 2,
p.
344.
Mocanu, Diana
2022.
Asymptotic Fermat for signatures (p,p,2)$(p,p,2)$ and (p,p,3)$(p,p,3)$ over totally real fields.
Mathematika,
Vol. 68,
Issue. 4,
p.
1233.
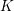 $K$ be a totally real field. By the asymptotic Fermat’s Last Theorem over
$K$ be a totally real field. By the asymptotic Fermat’s Last Theorem over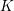 $K$ we mean the statement that there is a constant
$K$ we mean the statement that there is a constant 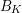 $B_{K}$ such that for any prime exponent
$B_{K}$ such that for any prime exponent 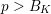 $p>B_{K}$, the only solutions to the Fermat equation
$p>B_{K}$, the only solutions to the Fermat equation 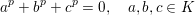 $$\begin{eqnarray}a^{p}+b^{p}+c^{p}=0,\quad a,b,c\in K\end{eqnarray}$$
$$\begin{eqnarray}a^{p}+b^{p}+c^{p}=0,\quad a,b,c\in K\end{eqnarray}$$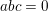 $abc=0$. With the help of modularity, level lowering and image-of-inertia comparisons, we give an algorithmically testable criterion which, if satisfied by
$abc=0$. With the help of modularity, level lowering and image-of-inertia comparisons, we give an algorithmically testable criterion which, if satisfied by 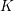 $K$, implies the asymptotic Fermat’s Last Theorem over
$K$, implies the asymptotic Fermat’s Last Theorem over 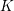 $K$. Using techniques from analytic number theory, we show that our criterion is satisfied by
$K$. Using techniques from analytic number theory, we show that our criterion is satisfied by 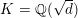 $K=\mathbb{Q}(\sqrt{d})$ for a subset of
$K=\mathbb{Q}(\sqrt{d})$ for a subset of 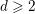 $d\geqslant 2$ having density
$d\geqslant 2$ having density 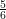 ${\textstyle \frac{5}{6}}$ among the squarefree positive integers. We can improve this density to
${\textstyle \frac{5}{6}}$ among the squarefree positive integers. We can improve this density to 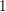 $1$ if we assume a standard ‘Eichler–Shimura’ conjecture.
$1$ if we assume a standard ‘Eichler–Shimura’ conjecture.