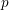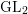Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Feigon, Brooke
Martin, Kimball
and
Whitehouse, David
2018.
Periods and nonvanishing of central L-values for GL(2n).
Israel Journal of Mathematics,
Vol. 225,
Issue. 1,
p.
223.
Xue, Hang
2021.
Epsilon dichotomy for linear models.
Algebra & Number Theory,
Vol. 15,
Issue. 1,
p.
173.
Li, Huajie
2021.
An infinitesimal variant of the Guo–Jacquet
trace formula, II.
Pacific Journal of Mathematics,
Vol. 315,
Issue. 1,
p.
151.
Xue, Hang
2022.
Orbital integrals on .
Canadian Journal of Mathematics,
Vol. 74,
Issue. 3,
p.
858.
Li, Huajie
2023.
A Local Trace Formula for p-adic Infinitesimal Symmetric Spaces: the Case of Guo–Jacquet.
International Mathematics Research Notices,
Vol. 2023,
Issue. 24,
p.
21581.
Xue, Hang
and
Zhang, Wei
2023.
Twisted Linear Periods and a New Relative Trace Formula.
Peking Mathematical Journal,