By an influential theorem of Boman, a function f$f$ on an open set U$U$ in \mathbb{R}^{d}$\mathbb{R}^{d}$ is smooth ({\mathcal{C}}^{\infty }${\mathcal{C}}^{\infty }$) if and only if it is arc-smooth, that is, f\,\circ \,c$f\,\circ \,c$ is smooth for every smooth curve c:\mathbb{R}\rightarrow U$c:\mathbb{R}\rightarrow U$. In this paper we investigate the validity of this result on closed sets. Our main focus is on sets which are the closure of their interior, so-called fat sets. We obtain an analogue of Boman’s theorem on fat closed sets with Hölder boundary and on fat closed subanalytic sets with the property that every boundary point has a basis of neighborhoods each of which intersects the interior in a connected set. If X\subseteq \mathbb{R}^{d}$X\subseteq \mathbb{R}^{d}$ is any such set and f:X\rightarrow \mathbb{R}$f:X\rightarrow \mathbb{R}$ is arc-smooth, then f$f$ extends to a smooth function defined on \mathbb{R}^{d}$\mathbb{R}^{d}$. We also get a version of the Bochnak–Siciak theorem on all closed fat subanalytic sets and all closed sets with Hölder boundary: if f:X\rightarrow \mathbb{R}$f:X\rightarrow \mathbb{R}$ is the restriction of a smooth function on \mathbb{R}^{d}$\mathbb{R}^{d}$ which is real analytic along all real analytic curves in X$X$, then f$f$ extends to a holomorphic function on a neighborhood of X$X$ in \mathbb{C}^{d}$\mathbb{C}^{d}$. Similar results hold for non-quasianalytic Denjoy–Carleman classes (of Roumieu type). We will also discuss sharpness and applications of these results.

In his work on deformation quantization of algebraic varieties Kontsevich introduced the notion of algebroid as a certain generalization of a sheaf of algebras. We construct algebroids which are given locally by NC-smooth thickenings in the sense of Kapranov, over two classes of smooth varieties: the bases of miniversal families of vector bundles on projective curves, and the bases of miniversal families of quiver representations.

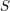Soient S$S$ un schéma nœthérien et 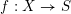f:X\rightarrow S$f:X\rightarrow S$ un morphisme propre. D’après SGA 4 XIV, pour tout faisceau constructible 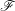\mathscr{F}$\mathscr{F}$ de 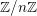\mathbb{Z}/n\mathbb{Z}$\mathbb{Z}/n\mathbb{Z}$-modules sur 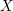X$X$, les faisceaux de 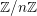\mathbb{Z}/n\mathbb{Z}$\mathbb{Z}/n\mathbb{Z}$-modules 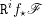\mathtt{R}^{i}f_{\star }\mathscr{F}$\mathtt{R}^{i}f_{\star }\mathscr{F}$, obtenus par image directe (pour la topologie étale), sont également constructibles : il existe une stratification 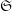\mathfrak{S}$\mathfrak{S}$ de 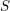S$S$ telle que ces faisceaux soient localement constants constructibles sur les strates. À la suite de travaux de N. Katz et G. Laumon, ou L. Illusie, dans le cas particulier où 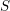S$S$ est génériquement de caractéristique nulle ou bien les faisceaux 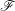\mathscr{F}$\mathscr{F}$ sont constants (de torsion inversible sur 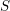S$S$), on étudie ici la dépendance de 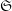\mathfrak{S}$\mathfrak{S}$ en 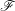\mathscr{F}$\mathscr{F}$. On montre qu’une condition naturelle de constructibilité et modération « uniforme » satisfaite par les faisceaux constants, introduite par O. Gabber, est stable par les foncteurs 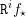\mathtt{R}^{i}f_{\star }$\mathtt{R}^{i}f_{\star }$. Si 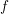f$f$ n’est pas supposé propre, ce résultat subsiste sous réserve de modération à l’infini, relativement à 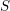S$S$. On démontre aussi l’existence de bornes uniformes sur les nombres de Betti, qui s’appliquent notamment pour les fibres des faisceaux 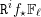\mathtt{R}^{i}f_{\star }\mathbb{F}_{\ell }$\mathtt{R}^{i}f_{\star }\mathbb{F}_{\ell }$, où 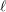\ell$\ell$ parcourt les nombres premiers inversibles sur 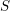S$S$.

We generalize the Cohen–Lenstra heuristics over function fields to étale group schemes G$G$ (with the classical case of abelian groups corresponding to constant group schemes). By using the results of Ellenberg–Venkatesh–Westerland, we make progress towards the proof of these heuristics. Moreover, by keeping track of the image of the Weil-pairing as an element of \wedge ^{2}G(1)$\wedge ^{2}G(1)$, we formulate more refined heuristics which nicely explain the deviation from the usual Cohen–Lenstra heuristics for abelian \ell$\ell$-groups in cases where \ell \mid q-1$\ell \mid q-1$; the nature of this failure was suggested already in the works of Malle, Garton, Ellenberg–Venkatesh–Westerland, and others. On the purely large random matrix side, we provide a natural model which has the correct moments, and we conjecture that these moments uniquely determine a limiting probability measure.

We consider families of Siegel eigenforms of genus 2$2$ and finite slope, defined as local pieces of an eigenvariety and equipped with a suitable integral structure. Under some assumptions on the residual image, we show that the image of the Galois representation associated with a family is big, in the sense that a Lie algebra attached to it contains a congruence subalgebra of non-zero level. We call the Galois level of the family the largest such level. We show that it is trivial when the residual representation has full image. When the residual representation is a symmetric cube, the zero locus defined by the Galois level of the family admits an automorphic description: it is the locus of points that arise from overconvergent eigenforms for \operatorname{GL}_{2}$\operatorname{GL}_{2}$, via a p$p$-adic Langlands lift attached to the symmetric cube representation. Our proof goes via the comparison of the Galois level with a ‘fortuitous’ congruence ideal. Some of the p$p$-adic lifts are interpolated by a morphism of rigid analytic spaces from an eigencurve for \operatorname{GL}_{2}$\operatorname{GL}_{2}$ to an eigenvariety for \operatorname{GSp}_{4}$\operatorname{GSp}_{4}$, while the remainder appear as isolated points on the eigenvariety.