Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T18:01:00.548Z Has data issue: false hasContentIssue false
  • English
  • Français

Galois level and congruence ideal for 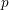$p$-adic families of finite slope Siegel modular forms

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  27 March 2019

Andrea Conti
Andrea Conti*
Affiliation:
Department of Mathematics and Statistics, Concordia University, 1400 De Maisonneuve Boulevard West, Montreal, Quebec, Canada H3G 1M8 email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider families of Siegel eigenforms of genus 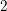$2$ and finite slope, defined as local pieces of an eigenvariety and equipped with a suitable integral structure. Under some assumptions on the residual image, we show that the image of the Galois representation associated with a family is big, in the sense that a Lie algebra attached to it contains a congruence subalgebra of non-zero level. We call the Galois level of the family the largest such level. We show that it is trivial when the residual representation has full image. When the residual representation is a symmetric cube, the zero locus defined by the Galois level of the family admits an automorphic description: it is the locus of points that arise from overconvergent eigenforms for 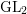$\operatorname{GL}_{2}$, via a 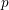$p$-adic Langlands lift attached to the symmetric cube representation. Our proof goes via the comparison of the Galois level with a ‘fortuitous’ congruence ideal. Some of the 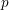$p$-adic lifts are interpolated by a morphism of rigid analytic spaces from an eigencurve for 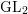$\operatorname{GL}_{2}$ to an eigenvariety for 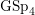$\operatorname{GSp}_{4}$, while the remainder appear as isolated points on the eigenvariety.

Keywords

Siegel modular formseigenvarietiesGalois representationsbig imagecongruence idealtrianguline representations

MSC classification

Primary: 11F80: Galois representations 11F33: Congruences for modular and $p$-adic modular forms 11F46: Siegel modular groups; Siegel and Hilbert-Siegel modular and automorphic forms
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 4 , April 2019 , pp. 776 - 831
Copyright
© The Author 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

Current address: Computational Arithmetic Geometry – IWR – Universität Heidelberg, Im Neuenheimer Feld 205, 69120 Heidelberg, Germany

The author was supported by the Programs ArShiFo ANR-10-BLAN-0114 and PerCoLaTor ANR-14-CE25-0002-01.

References

Andreatta, F., Iovita, A. and Pilloni, V., p-adic families of Siegel modular cuspforms , Ann. of Math. (2) 181 (2015), 623–697.10.4007/annals.2015.181.2.5Google Scholar
Andrianov, A. N., Quadratic Forms and Hecke Operators, Grundlehren der Mathematischen Wissenschaften, vol. 286 (Springer, Berlin, 1987).Google Scholar
Andrianov, A. N., Twisting of Siegel modular forms with characters, and L-functions , St. Petersburg Math. J. 20 (2009), 851–871.10.1090/S1061-0022-09-01076-0Google Scholar
Bellaïche, J., Eigenvarieties and adjoint  $p$ -adic  $L$ -functions, Preprint (2012).Google Scholar
Bellaïche, J. and Chenevier, G., Families of Galois representations and Selmer groups, Astérisque, vol. 324 (Société Mathématique de France, Paris, 2009).Google Scholar
Berger, L., Représentations p-adiques et équations différentielles , Invent. Math. 148 (2002), 219–284.Google Scholar
Berger, L., Trianguline representations , Bull. Lond. Math. Soc. 43 (2011), 619–635.10.1112/blms/bdr036Google Scholar
Berger, L. and Chenevier, G., Représentations potentiellement triangulines de dimension 2 , J. Théor. Nombres Bordeaux 22 (2010), 557–574.Google Scholar
Bijakowski, S., Pilloni, V. and Stroh, B., Classicité de formes modulaires surconvergentes , Ann. of Math. (2) 183 (2016), 975–1014.Google Scholar
Bosch, S., Güntzer, U. and Remmert, R., Non-Archimedean analysis, Grundlehren der Mathematischen Wissenschaften, vol. 261 (Springer, Berlin, 1984).10.1007/978-3-642-52229-1Google Scholar
Brasca, R. and Rosso, G., Eigenvarieties for non-cuspidal modular forms over certain PEL Shimura varieties, Preprint (2016), arXiv:1605.05065.Google Scholar
Buzzard, K., Eigenvarieties , in L-functions and Galois representations, London Mathematical Society Lecture Note Series, vol. 320 (Cambridge University Press, Cambridge, 2007), 59–120.10.1017/CBO9780511721267.004Google Scholar
Carayol, H., Formes modulaires et représentations galoisiennes à valeurs dans un anneau local complet , Contemp. Math. 165 (1994), 213–237.10.1090/conm/165/01601Google Scholar
Chenevier, G., Familles p-adiques de formes automorphes pour GL(n) , J. reine angew. Math. 570 (2004), 143–217.Google Scholar
Chenevier, G., Une correspondance de Jacquet–Langlands p-adique , Duke Math. J. 126 (2005), 161–194.Google Scholar
Coleman, R., Classical and overconvergent modular forms , Invent. Math. 124 (1996), 214–241.10.1007/s002220050051Google Scholar
Coleman, R. and Mazur, B., The eigencurve , in Galois representations in arithmetic algebraic geometry, London Mathematical Society Lecture Note Series, vol. 254 (Cambridge University Press, Cambridge, 1998), 1–113.Google Scholar
Colmez, P., Représentations triangulines de dimension 2 , in Représentations p-adiques de groupes p-adiques I : représentations galoisiennes et (𝜑, 𝛤)-modules, Astérisque, vol. 319 (Société Mathématique de France, Paris, 2008), 213–258.Google Scholar
Conrad, B., Irreducible components of rigid analytic spaces , Ann. Inst. Fourier (Grenoble) 49 (1999), 905–919.Google Scholar
Conti, A., Big Galois image for  $p$ -adic families of positive slope automorphic forms, PhD thesis, Université Paris 13 (2016).Google Scholar
Conti, A., Iovita, A. and Tilouine, J., Big image of Galois representations associated with finite slope p-adic families of modular forms , in Elliptic curves, modular forms and Iwasawa theory: In Honour of John H. Coates’ 70th Birthday, Cambridge, UK, March 2015, Proceedings in Mathematics & Statistics, vol. 188, eds Loeffler, D. and Zerbes, S. L. (Springer, New York, 2016), 87–124.10.1007/978-3-319-45032-2_3Google Scholar
Di Matteo, G., On admissible tensor products in p-adic Hodge theory , Compos. Math. 149 (2013), 417–429.Google Scholar
Di Matteo, G., On triangulable tensor products of  $B$ -pairs and trianguline representations, Preprint (2013).Google Scholar
Dimitrov, M. and Ghate, E., On classical weight one forms in Hida families , J. Théorie Nombres Bordeaux 24 (2012), 669–690.Google Scholar
Emerton, M., Local-global compatibility in the  $p$ -adic Langlands programme for  $\operatorname{GL}_{2/\mathbb{Q}}$ , Preprint (2014).Google Scholar
Faltings, G., Crystalline cohomology and Galois representations , in Algebraic analysis, geometry, and volume theory (Johns Hopkins University Press, Baltimore, MD, 1989), 25–80.Google Scholar
Fischman, A., On the image of 𝜆-adic Galois representations , Ann. Inst. Fourier (Grenoble) 52 (2002), 351–378.Google Scholar
Genestier, A. and Tilouine, J., Systèmes de Taylor–Wiles pour GSp4 , in Formes automorphes II. Le cas du groupe GSp(4), Astérisque, vol. 302 (Société Mathématique de France, Paris, 2005), 177–290.Google Scholar
Hansen, D., Universal eigenvarieties, trianguline Galois representations, and p-adic Langlands functoriality , J. Reine Angew. Math. 730 (2017), 1–64.10.1515/crelle-2014-0130Google Scholar
Hida, H., Big Galois representations and p-adic L-functions , Compos. Math. 151 (2015), 603–654.10.1112/S0010437X14007684Google Scholar
Hida, H. and Tilouine, J., Big image of Galois representations and congruence ideals , in Arithmetic and Geometry, eds Dieulefait, L., Faltings, G., Heath-Brown, D. R., Manin, Y. I., Moroz, B. Z. and Wintenberger, J.-P. (Cambridge University Press, Cambridge, 2015), 217–254.Google Scholar
de Jong, A. J., Crystalline Dieudonné theory via formal and rigid geometry , Publ. Math. Inst. Hautes Études Sci. 82 (1995), 5–96.10.1007/BF02698637Google Scholar
Kedlaya, K. S., Pottharst, J. and Xiao, L., Cohomology of arithmetic families of (𝜑, 𝛤)-modules , J. Amer. Math. Soc. 27 (2014), 1043–1115.Google Scholar
Kim, H. H. and Shahidi, F., Functorial products for GL2 × GL3 and the symmetric cube for GL2 , Ann. of Math. (2) 155 (2002), 837–893.Google Scholar
Kisin, M., Overconvergent modular forms and the Fontaine–Mazur conjecture , Invent. Math. (2003), 363–454.Google Scholar
Lang, J., On the image of the Galois representation associated to a non-CM Hida family , Algebra Number Theory 10 (2016), 155–194.Google Scholar
Livné, R., On the conductors of modulo ℓ representations coming from modular forms , J. Number Theory 31 (1989), 133–141.Google Scholar
Ludwig, J., p-adic functoriality for inner forms of unitary groups in three variables , Math. Res. Lett. 21 (2014), 141–148.Google Scholar
Mazur, B., Deforming Galois representations , in Galois groups over ℚ (Springer, Berlin, 1989), 385–437.Google Scholar
Momose, F., On the ℓ-adic representations attached to modular forms , J. Fac. Sci. Univ. Tokyo Sect. IA Math. 28 (1981), 89–109.Google Scholar
O’Meara, O. T., Symplectic groups, Mathematical Surveys, vol. 16 (American Mathematical Society, Providence, RI, 1978).Google Scholar
Pilloni, V., Modularité, formes de Siegel et surfaces abéliennes , J. reine angew. Math. 666 (2012), 35–82.Google Scholar
Pink, R., Compact subgroups of linear algebraic groups , J. Algebra 206 (1998), 438–504.Google Scholar
Ramakrishnan, D. and Shahidi, F., Siegel modular forms of genus 2 attached to elliptic curves , Math. Res. Lett. 14 (2007), 315–332.Google Scholar
Ribet, K., On ℓ-adic representations attached to modular forms , Invent. Math. 28 (1975), 245–276.Google Scholar
Ribet, K., On ℓ-adic representations attached to modular forms. II , Glasgow Math. J. 27 (1985), 185–194.Google Scholar
Rouquier, R., Caractérisation des caractères et pseudo-caractères , J. Algebra 180 (1996), 571–586.10.1006/jabr.1996.0083Google Scholar
Sen, S., Lie algebras of Galois groups arising from Hodge–Tate modules , Ann. of Math. (2) 97 (1973), 160–170.Google Scholar
Sen, S., Continuous cohomology and p-adic Hodge theory , Invent. Math. 62 (1980), 89–116.Google Scholar
Sen, S., An infinite dimensional Hodge–Tate theory , Bull. Soc. Math. France 121 (1993), 13–34.10.24033/bsmf.2199Google Scholar
Taylor, R., Galois representations associated to Siegel modular forms of low weight , Duke Math. J. 63 (1991), 281–332.Google Scholar
Tazhetdinov, S., Subnormal structure of symplectic groups over local rings , Math. Notes Acad. Sci. USSR 37 (1985), 164–169.Google Scholar
Urban, E., Sur les représentations p-adiques associées aux représentations cuspidales de GSp4(Q) , in Formes automorphes II. Le cas du groupe GSp(4), Astérisque, vol. 302 (Société Mathématique de France, Paris, 2005), 151–176.Google Scholar