Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-24T01:02:11.034Z Has data issue: false hasContentIssue false
  • English
  • Français

Cohen–Lenstra heuristics for étale group schemes and symplectic pairings

Part of: Connections with homological algebra and category theory Arithmetic algebraic geometry Special matrices Algebraic number theory: local and $p$-adic fields Curves

Published online by Cambridge University Press:  20 March 2019

Michael Lipnowski  and
Jacob Tsimerman
Michael Lipnowski
Affiliation:
Department of Mathematics, McGill University, Burnside Hall, Room 1005, 805 Sherbrooke Street West, Montreal, QC H3A 0B9, Canada email [email protected]
Jacob Tsimerman
Affiliation:
Department of Mathematics, University of Toronto, Bahen Centre, Room 6290, 40 St. George Street, Toronto, ON M5S 2E4, Canada email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We generalize the Cohen–Lenstra heuristics over function fields to étale group schemes 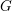$G$ (with the classical case of abelian groups corresponding to constant group schemes). By using the results of Ellenberg–Venkatesh–Westerland, we make progress towards the proof of these heuristics. Moreover, by keeping track of the image of the Weil-pairing as an element of 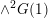$\wedge ^{2}G(1)$, we formulate more refined heuristics which nicely explain the deviation from the usual Cohen–Lenstra heuristics for abelian 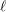$\ell$-groups in cases where 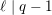$\ell \mid q-1$; the nature of this failure was suggested already in the works of Malle, Garton, Ellenberg–Venkatesh–Westerland, and others. On the purely large random matrix side, we provide a natural model which has the correct moments, and we conjecture that these moments uniquely determine a limiting probability measure.

Keywords

curves over finite fieldsCohen–Lenstra heuristicsp-adic random matrices

MSC classification

Primary: 11G20: Curves over finite and local fields 11S31: Class field theory; $p$-adic formal groups 20J05: Homological methods in group theory 14H10: Families, moduli (algebraic) 15B52: Random matrices
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 4 , April 2019 , pp. 758 - 775
Copyright
© The Authors 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Achter, J., The distribution of class groups of function fields , J. Pure Appl. Algebra 204 (2006), 316–333.10.1016/j.jpaa.2005.04.003Google Scholar
Bhargava, M., The density of discriminants of quartic rings and fields , Ann. of Math. (2) 162 (2005), 1031–1063.10.4007/annals.2005.162.1031Google Scholar
Cohen, H. and Lenstra, H., Heuristics on class groups of number fields , in Number theory, Noordwijkerhout 1983, Noordwijkerhout, 1983, Lecture Notes in Mathematics, vol. 1068 (Springer, Berlin, 1984), 33–62.10.1007/BFb0099440Google Scholar
Davenport, H. and Heilbronn, H., On the density of discriminants of cubic fields. II , Proc. R. Soc. Lond. Ser. A 322 (1971), 405–420.10.1098/rspa.1971.0075Google Scholar
Ellenberg, J. S., Venkatesh, A. and Westerland, C., Homological stability for Hurwitz spaces and the Cohen–Lenstra conjecture over function fields , Ann. of Math. (2) 183 (2016), 729–786.10.4007/annals.2016.183.3.1Google Scholar
Fouvry, E. and Klüners, J., On the 4-rank of class groups of quadratic number fields , Invent. Math. 167 (2007), 455–513.10.1007/s00222-006-0021-2Google Scholar
Friedman, E. and Washington, L., On the distribution of divisor class groups of curves over a finite field , in Théorie des nombres, Quebec, PQ, 1987 (de Gruyter, Berlin, 1989), 227–239.Google Scholar
Garton, D., Random matrices, Cohen–Lenstra heuristics, and roots of unity , Algebra Number Theory 9 (2015), 149–171.10.2140/ant.2015.9.149Google Scholar
Hall, C., Big symplectic or orthogonal monodromy modulo ℓ , Duke Math. J. 141 (2008), 179–203.10.1215/S0012-7094-08-14115-8Google Scholar
Klys, J., The distribution of $p$ -torsion in degree $p$ cyclic fields, Preprint (2016), arXiv:1610.00226v1.Google Scholar
Malle, G., On the distribution of class groups of number fields , Experiment. Math. 19 (2010), 465–474.10.1080/10586458.2010.10390636Google Scholar
Michael, A. A. G., Finite abelian actions on surfaces , Topology Appl. 153 (2006), 2591–2612.10.1016/j.topol.2005.05.010Google Scholar
Milovic, D. Z., On the 8-rank of narrow class groups of ℚ(√-4pp), ℚ(√-8pq), and ℚ(√8pq) , Int. J. Number Theory 14 (2018), 2165–2193.10.1142/S1793042118501300Google Scholar
Romagny, M. and Wewers, S., Hurwitz spaces , in Groupes de Galois arithmétiques et différentiels, Séminaire et Congrès, vol. 13 (Société Mathématique de France, Paris, 2006), 313–341.Google Scholar
Smith, A., Governing fields and statistics for 4-Selmer groups and 8-class groups, Preprint (2016), arXiv:1607.07860v1.Google Scholar
Wood, M. M., The distribution of sandpile groups of random graphs , J. Amer. Math. Soc. 30 (2017), 915–958.10.1090/jams/866Google Scholar
Yu, J.-K., Toward a proof of the Cohen–Lenstra conjecture in the function field case, Preprint (1997).Google Scholar