Article contents
Constructibilité et modération uniformes en cohomologie étale
Published online by Cambridge University Press: 19 March 2019
Abstract
Soient 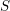 $S$ un schéma nœthérien et
$S$ un schéma nœthérien et 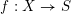 $f:X\rightarrow S$ un morphisme propre. D’après SGA 4 XIV, pour tout faisceau constructible
$f:X\rightarrow S$ un morphisme propre. D’après SGA 4 XIV, pour tout faisceau constructible 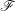 $\mathscr{F}$ de
$\mathscr{F}$ de 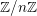 $\mathbb{Z}/n\mathbb{Z}$-modules sur
$\mathbb{Z}/n\mathbb{Z}$-modules sur 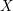 $X$, les faisceaux de
$X$, les faisceaux de 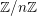 $\mathbb{Z}/n\mathbb{Z}$-modules
$\mathbb{Z}/n\mathbb{Z}$-modules 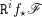 $\mathtt{R}^{i}f_{\star }\mathscr{F}$, obtenus par image directe (pour la topologie étale), sont également constructibles : il existe une stratification
$\mathtt{R}^{i}f_{\star }\mathscr{F}$, obtenus par image directe (pour la topologie étale), sont également constructibles : il existe une stratification 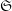 $\mathfrak{S}$ de
$\mathfrak{S}$ de 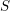 $S$ telle que ces faisceaux soient localement constants constructibles sur les strates. À la suite de travaux de N. Katz et G. Laumon, ou L. Illusie, dans le cas particulier où
$S$ telle que ces faisceaux soient localement constants constructibles sur les strates. À la suite de travaux de N. Katz et G. Laumon, ou L. Illusie, dans le cas particulier où 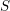 $S$ est génériquement de caractéristique nulle ou bien les faisceaux
$S$ est génériquement de caractéristique nulle ou bien les faisceaux 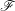 $\mathscr{F}$ sont constants (de torsion inversible sur
$\mathscr{F}$ sont constants (de torsion inversible sur 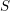 $S$), on étudie ici la dépendance de
$S$), on étudie ici la dépendance de 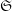 $\mathfrak{S}$ en
$\mathfrak{S}$ en 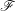 $\mathscr{F}$. On montre qu’une condition naturelle de constructibilité et modération « uniforme » satisfaite par les faisceaux constants, introduite par O. Gabber, est stable par les foncteurs
$\mathscr{F}$. On montre qu’une condition naturelle de constructibilité et modération « uniforme » satisfaite par les faisceaux constants, introduite par O. Gabber, est stable par les foncteurs 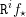 $\mathtt{R}^{i}f_{\star }$. Si
$\mathtt{R}^{i}f_{\star }$. Si 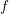 $f$ n’est pas supposé propre, ce résultat subsiste sous réserve de modération à l’infini, relativement à
$f$ n’est pas supposé propre, ce résultat subsiste sous réserve de modération à l’infini, relativement à 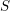 $S$. On démontre aussi l’existence de bornes uniformes sur les nombres de Betti, qui s’appliquent notamment pour les fibres des faisceaux
$S$. On démontre aussi l’existence de bornes uniformes sur les nombres de Betti, qui s’appliquent notamment pour les fibres des faisceaux 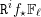 $\mathtt{R}^{i}f_{\star }\mathbb{F}_{\ell }$, où
$\mathtt{R}^{i}f_{\star }\mathbb{F}_{\ell }$, où 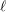 $\ell$ parcourt les nombres premiers inversibles sur
$\ell$ parcourt les nombres premiers inversibles sur 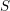 $S$.
$S$.
Let 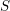 $S$ be a Noetherian scheme and
$S$ be a Noetherian scheme and 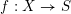 $f:X\rightarrow S$ a proper morphism. By SGA 4 XIV, for any constructible sheaf
$f:X\rightarrow S$ a proper morphism. By SGA 4 XIV, for any constructible sheaf 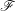 $\mathscr{F}$ of
$\mathscr{F}$ of 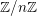 $\mathbb{Z}/n\mathbb{Z}$-modules on
$\mathbb{Z}/n\mathbb{Z}$-modules on 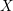 $X$, the sheaves of
$X$, the sheaves of 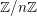 $\mathbb{Z}/n\mathbb{Z}$-modules
$\mathbb{Z}/n\mathbb{Z}$-modules 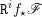 $\mathtt{R}^{i}f_{\star }\mathscr{F}$ obtained by direct image (for the étale topology) are themselves constructible, that is, there is a stratification
$\mathtt{R}^{i}f_{\star }\mathscr{F}$ obtained by direct image (for the étale topology) are themselves constructible, that is, there is a stratification 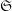 $\mathfrak{S}$ of
$\mathfrak{S}$ of 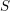 $S$ on whose strata these sheaves are locally constant constructible. After previous work of N. Katz and G. Laumon, or L. Illusie, on the special case in which
$S$ on whose strata these sheaves are locally constant constructible. After previous work of N. Katz and G. Laumon, or L. Illusie, on the special case in which 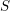 $S$ is generically of characteristic zero or the sheaves
$S$ is generically of characteristic zero or the sheaves 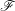 $\mathscr{F}$ are constant (with invertible torsion on
$\mathscr{F}$ are constant (with invertible torsion on 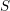 $S$), here we study the dependency of
$S$), here we study the dependency of 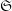 $\mathfrak{S}$ on
$\mathfrak{S}$ on 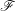 $\mathscr{F}$. We show that a natural ‘uniform’ tameness and constructibility condition satisfied by constant sheaves, which was introduced by O. Gabber, is stable under the functors
$\mathscr{F}$. We show that a natural ‘uniform’ tameness and constructibility condition satisfied by constant sheaves, which was introduced by O. Gabber, is stable under the functors 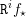 $\mathtt{R}^{i}f_{\star }$. If
$\mathtt{R}^{i}f_{\star }$. If 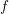 $f$ is not proper, this result still holds assuming tameness at infinity, relative to
$f$ is not proper, this result still holds assuming tameness at infinity, relative to 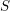 $S$. We also prove the existence of uniform bounds on Betti numbers, in particular for the stalks of the sheaves
$S$. We also prove the existence of uniform bounds on Betti numbers, in particular for the stalks of the sheaves 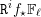 $\mathtt{R}^{i}f_{\star }\mathbb{F}_{\ell }$, where
$\mathtt{R}^{i}f_{\star }\mathbb{F}_{\ell }$, where 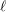 $\ell$ ranges through all prime numbers invertible on
$\ell$ ranges through all prime numbers invertible on 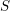 $S$.
$S$.
Keywords
- Type
- Research Article
- Information
- Copyright
- © The Author 2019
References
Sigles
Éléments de mathématique
Éléments de géométrie algébrique
Séminaires de géométrie algébrique
Séminaire sur les travaux de Gabber
Autres références
- 3
- Cited by


