Let

where λ is rational and not an integer. The author investigates lower estimates for example for

where the αi are distinct rational numbers not 0, and where x1, …, xk, are integers and

In recent years fixed point theorems have been proved for non-expansive and similar mappings on uniformly convex Banach spaces. The only role the linear structure plays in the statement of these results occurs in the definition of uniform convexity. It is therefore natural to ask whether the results depend essentially on the linear structure, or whether an extension of the notion of uniform convexity to metric spaces would allow the hypothesis of linear structure on the underlying space to be removed.

It is shown that every finitely generated field K of characteristic 0 may be embedded in infinitely many p-adic fields in such a way that the images of any given finite set C of non-zero elements of K are p-adic units. The result is suggested by Lech's proof of his generalization of Mahler's theorem on recurrent sequences. It also provides a simple proof of Selberg's theorem about torsion-free normal subgroups of matrix groups.

The purpose of this paper is to show that a well-known method for constructing “queer” sets in models of ZF set theory is also applicable to certain algebraic structures. An infinite set is called “quasi-minimal” if every subset of it is either finite or cofinite. In Section 1 I set out the two systems of set theory to be used in this paper, and illustrate the technique in its most fundamental form by constructing a model of set theory containing a quasi-minimal set. In Section 2 I show that by choosing the parameters appropriately, one can use this technique to obtain models of set theory containing groups whose carriers are quasi-minimal. In the third section various independence results are deduced from the existence of such models: in particular, it is shown that it is possible in ZF set theory to have an infinite group that satisfies both the ascending and descending chain conditions. The quasi-minimal groups constructed in Section 2 were all elementary abelian; in Section 4 it is shown that this was not just chance, but that in fact all quasi-minimal groups must be of this type. Finally in Section 5 permutations and permutation groups on quasi-minimal sets are examined.

A projection morphism ρ: G1 → G2 of finite graphs maps the vertex-set of G1 onto the vertex-set of G2, and preserves adjacency. As an example, if each vertex v of the dodecahedron graph D is identified with its unique antipodal vertex v¯ (which has distance 5 from v) then this induces an identification of antipodal pairs of edges, and gives a (2:1)-projection p: D → P where P is the Petersen graph.

In this paper a category-theoretical approach to graphs is used to define and study such double cover projections. An upper bound is found for the number of distinct double covers ρ: G1 → G2 for a given graph G2. A classification theorem for double cover projections is obtained, and it is shown that the n–dimensional octahedron graph K2,2,…,2 plays the role of universal object.

A code not requiring a distinct symbol to separate words is called comma-free. Two codes are isomorphic if one can be obtained from the other by a permutation of the underlying alphabet. Since subcodes of comma-free codes are comma-free, we investigate only maximal comma-free codes. All isomorphism classes of maximal comma-free codes with words of length 2 are determined and a natural representative of each class is given.

Some fixed point results are derived for mappings of contractive type in metric and topological spaces.

A question of John S. Wilson concerning indecomposable representations of metabelian groups satisfying the minimal condition for normal subgroups is answered negatively, by means of an example. It is shown that such representations need not be irreducible, even when the group being represented is an extension of an elementary abelian p–group by a quasicyclic q–group of the type first described by V.S. Čarin, and the characteristic of the field is a prime distinct from both p and q. This implies that certain techniques used in the study of metabelian groups satisfying the minimal condition for normal subgroups are not available for the corresponding class of soluble groups of derived length 3.

In the Appendix to a recent paper by J.J. Koliha and A.P. Leung (Math. Ann.216 (1975), 273–284), a functional calculus for continuous affine operators was constructed on the basis of the Taylor-Dunford calculus. This calculus applied only to functions defined and analytic in an open set containing the spectrum of an operator and the point λ = 1. In the present paper I examine the affine resolvent, and develop independently a more general calculus applicable to functions which are analytic in any open neighbourhood of the spectrum of an affine operator.

Let G1 and G2 be graphs and h1, h2 be hamiltonian paths (h-paths) in G1 and G2 respectively. The hamiltonian product (G1, h2)*(G2, h2) was defined by Holton. If a hamiltonian cycle exists in G2, it can give rise to 2nh-paths. Peckham conjectured that (G1, h1)*(G2, h2)≡(G1, h1)*(G2, h3) where h2 and h3 are any two of these 2nh-paths of G2. He has proved the validity of this conjecture for those h2, h3 where h3 is obtainable from h2 by a rotation along the h-cycle of G2. Here we disprove this conjecture for those h2, h3 where one is obtained from the other by a reflection of the h-cycle.

There is a group defined by fourth powers which did not yield to attempts to determine its order by coset enumerations. This group has now been shown to be infinite with the aid of a computer. An outline of the method is given as well as a simple direct proof inspired by the results of further computer calculations.

Recently Kurt Mahler asked: for which natural numbers N is the least common multiple of all the binomial coefficients the product of the primes less than or equal to N? We obtain a formula for the least common multiple of all the binomial coefficients of any natural number N and hence show that 2,11, and 23 are the only soultions to Mahler's problem.

A powerful tool in the construction of orthogonal designs has been amicable orthogonal designs. Recent results in the construction of Hadamard matrices has led to the need to find amicable orthogonal designs A, B in order n and of types (u1, U2, …, u6) and (ν1, ν2, …, νr) respectively satisfying At = -A, Bt = B, and ABt = BAt with

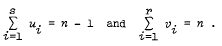
For simplicity, we say A, B are amicable orthogonal designs of type (u1, u2, …, us; v1, v2, …, vr).

We completely answer the question in order 8 by showing (1, 2, 2, 2; 8), (1, 2, 4; 2, 2, 4), (2, 2, 3; 2, 6), (7, 1, 7) and those designs derived from the above are the only possible.

We use our results to obtain new orthogonal designs in order 32.