We establish upper bounds for the distance to finite-dimensional subspaces in inner product spaces and improve some generalisations of Bessel's inequality obtained by Boas, Bellman and Bombieri. Refinements of the Hadamard inequality for Gram determinants are also given.

In this paper, we consider the nonhomogeneous semilinear elliptic equation

,

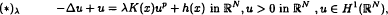where λ ≥ 0, 1 < p < (N + 2)/(N − 2), if N ≥ 3, 1 < p < ∞, if N = 2, h(x) ∈ H−l(ℝN), 0 ≢ h(x) ≥ 0 in ℝN, K(x) is a positive, bounded and continuous function on ℝN. We prove that if K(x) ≥ K∞ > 0 in ℝN, and lim∣x∣⃗∞K(x) = K∞, then there exists a positive constant λ✶ such that (✶)λ has at least two solutions if λ ∈ (0, λ✶) and no solution if λ > λ✶. Furthermore, (✶)λ has a unique solution for λ = λ✶ provided that h(x) satisfies some suitable conditions. We also obtain some further properties and bifurcation results of the solutions of (1.1)λ at λ = λ✶.

We establish a Banach space version of a theorem of Suzuki [8]. More precisely we prove that if X is a uniformly convex Banach space with a weakly continuous duality map (for example, lp for 1 < p < ∞), if C is a closed convex subset of X, and if F = {T (t): t ≥ 0} is a contraction semigroup on C such that Fix(F) ≠ ∅, then under certain appropriate assumptions made on the sequences {αn} and {tn} of the parameters, we show that the sequence {xn} implicitly defined by

for all n ≥ 1 converges strongly to a member of Fix(F).

If G is finite group and P is a Sylow p-subgroup of G, we prove that there is a unique largest normal subgroup L of G such that L ⋂ P = L ⋂ NG (P). If G is p-solvable, then L is the intersection of the kernels of the irreducible Brauer characters of G of degree not divisible by p.

We shown the rationality of the Taylor coefficients of the inverse of the Schwarz triangle functions for a triangle group about any vertex of the fundamental domain.

In an earlier article we obtain a sharp inequality for an arbitrary isometric immersion from a Riemannian manifold admitting a Riemannian submersion with totally geodesic fibres into a unit sphere. In this article we investigate the immersions which satisfy the equality case of the inequality. As a by-product, we discover a new characterisation of Cartan hypersurface in S4.

A radical α in the universal class of all associative rings is called matric-extensible if for all natural numbers n and all rings A, A ∈ α if and only if Mn(A) ∈ α, where Mn(A) denotes the n × n matrix ring with entries from A. We show that there are no coatoms, that is, maximal elements in the lattice of all matric-extensible radicals of associative rings.

Let A ∈ B(H) be a bounded non-compact operator that is not semi-Fredholm. The similarity invariant semigroup generated by A is shown to consist of all operators that are not semi-Fredholm and satisfy obvious inequalities for the nullity and co-nullity.

In previous papers, we used abstract potential theory, as developed by Fuglede and Ohtsuka, to a systematic treatment of rendezvous numbers. We considered Chebyshev constants and energies as two variable set functions, and introduced a modified notion of rendezvous intervals which proved to be rather nicely behaved even for only lower semicontinuous kernels or for not necessarily compact metric spaces.

Here we study the rendezvous and average numbers of possibly infinite dimensional normed spaces. It turns out that very general existence and uniqueness results hold for the modified rendezvous numbers in all Banach spaces. We also observe the connections of these magical numbers to Chebyshev constants, Chebyshev radius and entropy. Applying the developed notions with the available methods we calculate the rendezvous numbers or rendezvous intervals of certain concrete Banach spaces. In particular, a satisfactory description of the case of Lp spaces is obtained for all p > 0.

We show that some results of the Hutchinson-Barnsley theory for finite iterated function systems can be carried over to the infinite case. Namely, if {Fi : i ∈ ℕ} is a family of Matkowski's contractions on a complete metric space (X, d) such that (Fix0)i∈N is bounded for some x0 ∈ X, then there exists a non-empty bounded and separable set K which is invariant with respect to this family, that is, . Moreover, given σ ∈ ℕℕ and x ∈ X, the limit exists and does not depend on x. We also study separately the case in which (X, d) is Menger convex or compact. Finally, we answer a question posed by Máté concerning a finite iterated function system {F1,…, FN} with the property that each of Fi has a contractive fixed point.

Let

where ψ denotes the logarithmic derivative of Euler's gamma function. We prove that the functional inequality

holds if and only if 0 < r ≤ 1. And, we show that the converse is valid if and only if r < 0 or r ≥ n + 1.

The recovery of flow curves for non-Newtonian fluids from Couette rheometry measurements involves the solution of a quite simple first kind Volterra integral equation with a discontinuous kernel for which the solution, as a summation of an infinite series, has been known since 1953. Various methods, including an Euler-Maclaurin sum formula, have been proposed for the estimation of the value of the summation. They all involve the numerical differentiation of the observational data. In this paper, the properties of Bernoulli polynomials, in conjunctions with the special structure of the integral equation, are exploited to derive a parametric family of representations for its solution. They yield formulas similar to, but more general than, the previously published Euler-Maclaurin sum formula representations. The parameterisation is then utilised to derive two new classes of approximations. The first yields a family of finite difference approximations, which avoids the direct numerical differentiation of the observational data, while the second generates a framework for the construction of improved power law approximations.

Recently Calegari and Emerton made a conjecture about the 3-class groups of certain pure cubic fields and their normal closures. This paper proves their conjecture and provides additional insight into the structure of the 3-class groups of pure cubic fields and their normal closures.

We show that, for any positive integers n and m, if a set S ⊂ Rm intersects every m − 1 dimensional affine hyperplane in Rm in exactly n points, then S is not an Fσ set. This gives a natural extension to results of Khalid Bouhjar, Jan J. Dijkstra, and R. Daniel Mauldin, who have proven this result for the case when m = 2, and also Jan J. Dijkstra and Jan van Mill, who have shown this result for the case when n = m.

Let R be a commutative ring possessing (non-zero) zero-divisors. There is a natural graph associated to the set of zero-divisors of R. In this article we present a characterisation of two types of R. Those for which the associated zero-divisor graph has diameter different from 3 and those R for which the associated zero-divisor graph has girth other than 3. Thus, in a sense, for a generic non-domain R the associated zero-divisor graph has diameter 3 as well as girth 3.

In a recent paper we have shown that most non-expansive Lipschitz functions (in the sense of Baire's category) have a maximal Clarke subdifferential. In the present paper, we show that in a separable Banach space the set of non-expansive Lipschitz functions with a maximal Clarke subdifferential is not only generic, but also staunch in the space of non-expansive functions.