Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T02:20:01.674Z Has data issue: false hasContentIssue false
  • English
  • Français

Bifurcation of positive entire solutions for a semilinear elliptic equation

Published online by Cambridge University Press:  17 April 2009

Tsing-San Hsu  and
Huei-Li Lin
Tsing-San Hsu
Affiliation:
Center for General Education Chang Gung University, Kwei-San, Tao-Yuan 333, Taiwan, Republic of China
Huei-Li Lin
Affiliation:
Center for General Education Chang Gung University, Kwei-San, Tao-Yuan 333, Taiwan, Republic of China
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we consider the nonhomogeneous semilinear elliptic equation

,

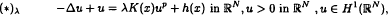where λ ≥ 0, 1 < p < (N + 2)/(N − 2), if N ≥ 3, 1 < p < ∞, if N = 2, h(x) ∈ H−l(ℝN), 0 ≢ h(x) ≥ 0 in ℝN, K(x) is a positive, bounded and continuous function on ℝN. We prove that if K(x) ≥ K∞ > 0 in ℝN, and lim∣x∣⃗∞K(x) = K∞, then there exists a positive constant λ✶ such that (✶)λ has at least two solutions if λ ∈ (0, λ✶) and no solution if λ > λ✶. Furthermore, (✶)λ has a unique solution for λ = λ✶ provided that h(x) satisfies some suitable conditions. We also obtain some further properties and bifurcation results of the solutions of (1.1)λ at λ = λ✶.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 72 , Issue 3 , December 2005 , pp. 349 - 370
Copyright
Copyright © Australian Mathematical Society 2005

References

[1]Amann, H., ‘Fixed point equations and nonlinear eigenvalue problems in ordered Banach spaces’, SIAM. Rev. 18 (1976), 620–709.CrossRefGoogle Scholar
[2]Ambrosetti, A. and Rabinowitz, P.H., ‘Dual variational method in critical point theory and applications’, J. Funct. Anal. 14 (1973), 349–381.CrossRefGoogle Scholar
[3]Bahri, A. and Lions, P.L., ‘On the existence of a positive solution of semilinear elliptic equations in unbounded domains,’ Ann. Inst. H. Poincaré Anal. Non Linéaire 14 (1997), 365–413.CrossRefGoogle Scholar
[4]Benci, V. and Cerami, G., ‘Positive solutions of some nonlinear elliptic problems in unbounded domains’, Arch. Rational Mech. Anal. 99 (1987), 283–300.CrossRefGoogle Scholar
[5]Berestycki, H. and Lions, P.L., ‘Nonlinear scalar field equations, I. Existence of a ground state’, Arch. Rational. Mech. Anal. 82 (1983), 313–345.CrossRefGoogle Scholar
[6]Cao, D.M. and Zhou, Z.H., ‘Multiple positive solutions of nonhomogeneous elliptic equations in ℝN,’ Proc. Roy. Soc. Edinburgh Sect. A 126 (1996), 443–463.Google Scholar
[7]Crandall, M.G. and Rabinowitz, P.H., ‘Bifurcation, perturbation of simple eigenvalues and lineaized stability’, Arch. Rational Mech. Anal. 52 (1973), 161–180.CrossRefGoogle Scholar
[8]Ding, W.Y. and Ni, W.M., ‘On the existence of entire solution of a semilinear elliptic equation’, Arch. Rational Mech. Anal. 91 (1986), 283–308.CrossRefGoogle Scholar
[9]Ekeland, L., ‘Nonconvex minimization problems’, Bull. Amer. Math. Soc. 1 (1979), 443–474.CrossRefGoogle Scholar
[10]Gilbarg, D. and Trudinger, N.S., Elliptic partial differential equations of second order (Springer-Verlag, New York, 1983).Google Scholar
[11]Hsu, T.S., ‘Existence and bifurcation of the positive solutions for a semilinear elliptic problem in exterior domains’, (preprint).Google Scholar
[12]Korman, P.L., Li, Y., and Ouyang, T.-C., ‘Exact multiplicity results for boundary value problems with nonlinearities generalizing cubic,’ Proc. Royal Soc. Edinbburgh Ser. A 126 (1996), 599–616.CrossRefGoogle Scholar
[13]Lions, P.L., ‘The concentration-compactness principle in the calculus of variations. The locally compact case’, Ann. Inst. H. Poincaré Anal. Non Linéaire 1 (1984), 109–145 and 223–283.CrossRefGoogle Scholar
[14]Lions, P.L., ‘On positive solutions of semilinear elliptic equations in unbounded domains’, in Nonlinear Diffusion Equations and Their Equilibrium States, (Ni, W.M., Peletier, L.A. and Serrin, J., Editors) (Springer-Veflag, New York, Berlin, 1988).Google Scholar
[15]Strauss, W., ‘Existence of solitary waves in higher dimensions’, Comm. Math. Phys. 55 (1977), 149–162.CrossRefGoogle Scholar
[16]Zhu, X.P., ‘A perturation result on positive entire solutions of a semilinear elliptic equation,’ J. Differential Equations 92 (1991), 163–178.CrossRefGoogle Scholar
[17]Zhu, X.P. and Cao, D.M., ‘The concentration-compactness principle in nonlinear elliptic equation’, Acta. Math. Sci. 9 (1989), 307–328.CrossRefGoogle Scholar
[18]Zhu, X.P. and Zhou, H.S., ‘Existence of multiple positive solutions of inhomogenous semilinear elliptic problems in unbounded domains,’ Proc. Roy. Soc. Edinburgh Sect. A 115 (1990), 301–318.CrossRefGoogle Scholar